半分手動の分散分析

1元配置分散分析を半分手動でやってみます。

データ

palmerpenguinsのデータを使って、bill_length_mmがspeciesにより異なるかどうかを検定します。

library(palmerpenguins)
library(dplyr)
## 
##  次のパッケージを付け加えます: 'dplyr'
##  以下のオブジェクトは 'package:stats' からマスクされています:
## 
##     filter, lag
##  以下のオブジェクトは 'package:base' からマスクされています:
## 
##     intersect, setdiff, setequal, union
library(ggplot2)

前処理

まず、missing completely at random (MCAR) を仮定して、欠測値のある行を除きます。

penguins2 <- penguins %>%
  select(species, bill_length_mm) %>%
  filter(!is.na(bill_length_mm))

可視化

箱ヒゲ図にしてみます。

ggplot(penguins2) +
  geom_boxplot(aes(x = species, y = bill_length_mm))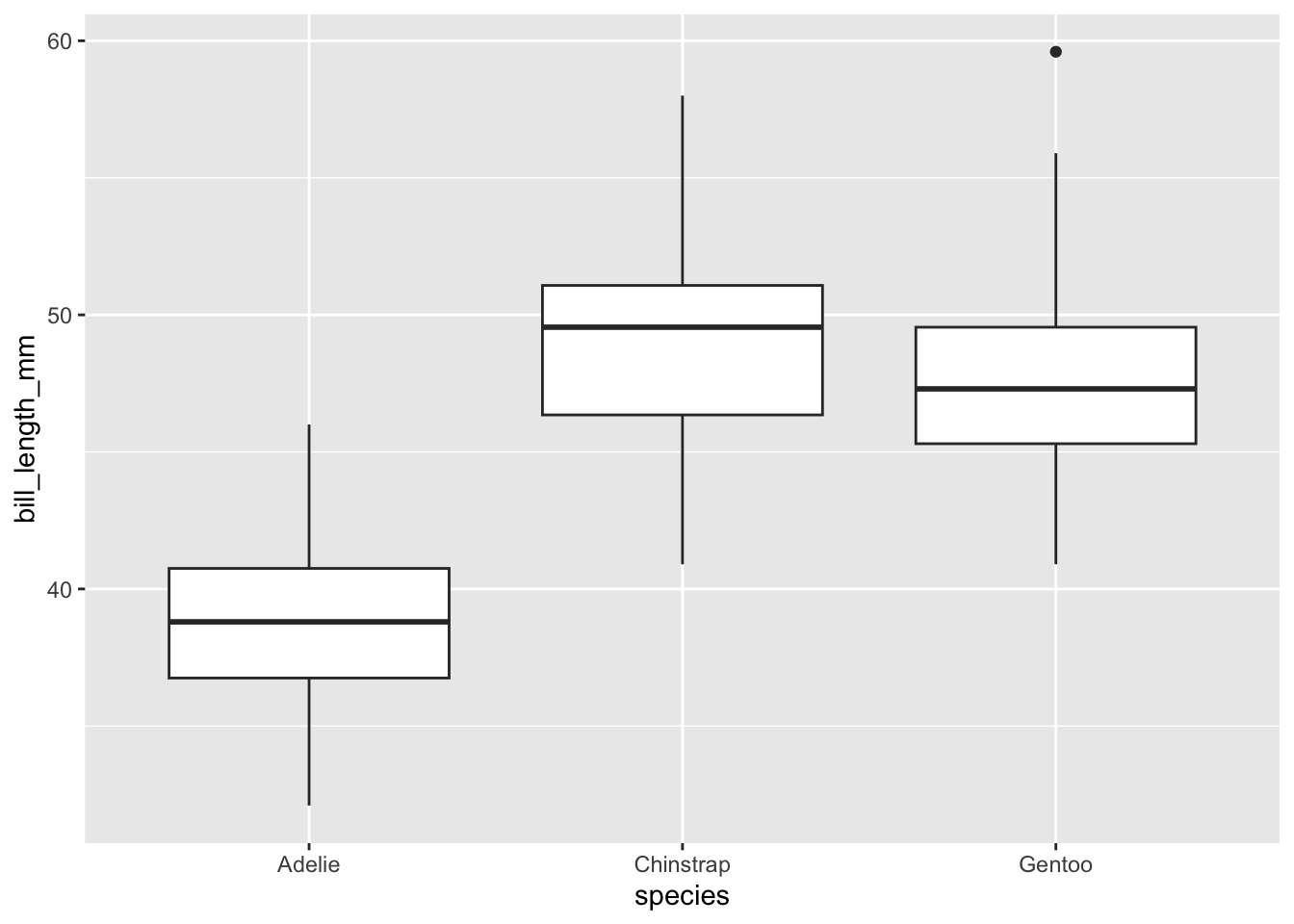

半分手動の分散分析

まず、全体平均を求めます。

(total_mean <- mean(penguins2$bill_length_mm))
## [1] 43.92193

各種(水準)ごとの観測数(n)と平均(mean)、偏差平方和(sumsq)を求めます。

(penguins3 <- penguins2 %>%
   group_by(species) %>%
   summarise(n = n(),
             mean = mean(bill_length_mm),
             sumsq =  n * (mean - total_mean)^2))
## # A tibble: 3 × 4
##   species       n  mean sumsq
##   <fct>     <int> <dbl> <dbl>
## 1 Adelie      151  38.8 3975.
## 2 Chinstrap    68  48.8 1641.
## 3 Gentoo      123  47.5 1579.

水準間平方和を求めます。

(sumsq_species <- penguins3 %>%
   pull(sumsq) %>%
   sum())
## [1] 7194.317

残差平方和を求めます。

(sumsq_resid <- penguins2 %>%
   left_join(penguins3, by = "species") %>%
   mutate(sq_resid = (bill_length_mm - mean)^2) %>%
   pull(sq_resid) %>%
   sum())
## [1] 2969.888

自由度を求めます。

(df_species <-  levels(penguins2$species) %>%
   length() - 1)
## [1] 2

(df_resid <- nrow(penguins2) - df_species - 1)
## [1] 339

平均平方を求めます。

(mean_sq_species <- sumsq_species / df_species)
## [1] 3597.159

(mean_sq_resid <- sumsq_resid / df_resid)
## [1] 8.760732

F値を求めます。

(F_value <- mean_sq_species / mean_sq_resid)
## [1] 410.6003

最後にp値を求めます。

(pf(F_value, df_species, df_resid, lower.tail = FALSE))
## [1] 2.694614e-91

aov関数による分散分析

aov関数の結果と比較してみます。

aov(bill_length_mm ~ species, data = penguins2) %>%
  summary()
##              Df Sum Sq Mean Sq F value Pr(>F)    
## species       2   7194    3597   410.6 <2e-16 ***
## Residuals   339   2970       9                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1