library(MASS)
library(ggplot2)
library(parallel)
options(mc.cores = 4)ちょうど1年前に、「いつでもAICを使えばよいというものではない」という発表資料を公開したのですが、あらためて関連した話をかいてみました。
生態学や森林科学の論文では、回帰分析の際、AICでモデル選択をおこなってから、選択された「ベストモデル」で係数の有意性を検定しているという例をよくみかけます。しかし、これには問題があります。
実例1
以下のようなデータを想定します。20個の変数(\(x_1, x_2, x_3, \dots, x_{20}\))がありますが、目的変数\(y\)と関係があるのは\(x_3\)だけという設定です。
\[ x_i \sim \mathrm{Normal}(0, 1), \quad i \in (1,2,3,\dots,20) \]
\[ y = x_3 + \epsilon, \quad \epsilon \sim \mathrm{Normal}(0, 1) \]
モデルは、すべての\(x\)を説明変数として組み込みます。
\[ y \sim x_1 + x_2 + x_3 + \dots + x_{20} \]
試行例
まずは1回だけのシミュレーションをやってみます。
データを生成します。サンプルサイズ(N)は100(あとで分割します)としています。
set.seed(1234)
N <- 100
num_x <- 20
x <- rnorm(N * num_x, 0, 1)
d <- matrix(x, ncol = num_x) |>
data.frame()
colnames(d) <- paste0("x", 1:num_x)
d$y <- d$x3 + rnorm(N, 0, 1)データを、当てはめ用と検証用に2分割します。サンプルサイズはそれぞれで50となります。
N2 <- floor(N / 2)
d1 <- d[1:N2, ]
d2 <- d[(N2 + 1):N, ]AICによるモデル選択
モデル式fを組立てて、MASSパッケージのstepAIC関数でAIC最小モデルを探索します。
f <- reformulate(paste0("x", 1:num_x), response = "y")
fit_lm <- lm(f, data = d1)
mod_aic_min <- stepAIC(fit_lm)
## Start: AIC=34.78
## y ~ x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10 + x11 +
## x12 + x13 + x14 + x15 + x16 + x17 + x18 + x19 + x20
##
## Df Sum of Sq RSS AIC
## - x12 1 0.0027 43.283 32.786
## - x16 1 0.0135 43.293 32.799
## - x2 1 0.0138 43.294 32.799
## - x18 1 0.0328 43.313 32.821
## - x7 1 0.0391 43.319 32.828
## - x9 1 0.0484 43.328 32.839
## - x15 1 0.0509 43.331 32.842
## - x8 1 0.1425 43.422 32.948
## - x11 1 0.1580 43.438 32.966
## - x20 1 0.3016 43.582 33.131
## - x1 1 0.4659 43.746 33.319
## - x6 1 0.4692 43.749 33.322
## - x13 1 0.6172 43.897 33.491
## - x14 1 0.6985 43.978 33.584
## - x19 1 1.3025 44.582 34.266
## - x10 1 1.7214 45.001 34.733
## <none> 43.280 34.783
## - x4 1 1.7915 45.071 34.811
## - x17 1 2.2854 45.565 35.356
## - x5 1 7.0175 50.297 40.297
## - x3 1 28.2589 71.539 57.911
##
## Step: AIC=32.79
## y ~ x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10 + x11 +
## x13 + x14 + x15 + x16 + x17 + x18 + x19 + x20
##
## Df Sum of Sq RSS AIC
## - x16 1 0.0122 43.295 30.800
## - x2 1 0.0124 43.295 30.801
## - x18 1 0.0324 43.315 30.824
## - x7 1 0.0380 43.321 30.830
## - x9 1 0.0631 43.346 30.859
## - x15 1 0.0756 43.358 30.874
## - x11 1 0.1594 43.442 30.970
## - x8 1 0.1648 43.447 30.976
## - x20 1 0.3708 43.653 31.213
## - x1 1 0.4737 43.756 31.331
## - x13 1 0.6759 43.959 31.561
## - x14 1 0.6970 43.980 31.585
## - x6 1 0.7243 44.007 31.616
## - x19 1 1.3595 44.642 32.333
## <none> 43.283 32.786
## - x4 1 1.8128 45.095 32.838
## - x10 1 1.9014 45.184 32.936
## - x17 1 2.4865 45.769 33.579
## - x5 1 7.0767 50.359 38.358
## - x3 1 28.5325 71.815 56.104
##
## Step: AIC=30.8
## y ~ x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10 + x11 +
## x13 + x14 + x15 + x17 + x18 + x19 + x20
##
## Df Sum of Sq RSS AIC
## - x2 1 0.0108 43.306 28.813
## - x18 1 0.0230 43.318 28.827
## - x7 1 0.0342 43.329 28.840
## - x9 1 0.0613 43.356 28.871
## - x15 1 0.0808 43.376 28.894
## - x8 1 0.1675 43.462 28.993
## - x11 1 0.1846 43.479 29.013
## - x20 1 0.3603 43.655 29.215
## - x1 1 0.4718 43.767 29.342
## - x13 1 0.6653 43.960 29.563
## - x6 1 0.7182 44.013 29.623
## - x14 1 0.7918 44.087 29.707
## - x19 1 1.3551 44.650 30.341
## <none> 43.295 30.800
## - x4 1 1.8054 45.100 30.843
## - x10 1 1.8948 45.190 30.942
## - x17 1 2.4898 45.785 31.596
## - x5 1 7.0647 50.359 36.358
## - x3 1 28.5867 71.882 54.150
##
## Step: AIC=28.81
## y ~ x1 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10 + x11 + x13 +
## x14 + x15 + x17 + x18 + x19 + x20
##
## Df Sum of Sq RSS AIC
## - x18 1 0.0209 43.327 26.837
## - x7 1 0.0328 43.338 26.851
## - x9 1 0.0611 43.367 26.883
## - x15 1 0.0766 43.382 26.901
## - x8 1 0.1571 43.463 26.994
## - x11 1 0.1814 43.487 27.022
## - x20 1 0.3534 43.659 27.219
## - x1 1 0.4766 43.782 27.360
## - x6 1 0.7142 44.020 27.631
## - x13 1 0.7715 44.077 27.696
## - x14 1 0.7817 44.087 27.707
## - x19 1 1.3699 44.676 28.370
## <none> 43.306 28.813
## - x4 1 1.8038 45.109 28.853
## - x10 1 2.0107 45.316 29.082
## - x17 1 2.5525 45.858 29.676
## - x5 1 7.4157 50.721 34.716
## - x3 1 29.3799 72.685 52.706
##
## Step: AIC=26.84
## y ~ x1 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10 + x11 + x13 +
## x14 + x15 + x17 + x19 + x20
##
## Df Sum of Sq RSS AIC
## - x7 1 0.0356 43.362 24.878
## - x9 1 0.0460 43.373 24.890
## - x15 1 0.0780 43.405 24.927
## - x8 1 0.1592 43.486 25.020
## - x11 1 0.1645 43.491 25.027
## - x20 1 0.3636 43.690 25.255
## - x1 1 0.4809 43.807 25.389
## - x14 1 0.7784 44.105 25.727
## - x6 1 0.7790 44.106 25.728
## - x13 1 0.8552 44.182 25.814
## - x19 1 1.3575 44.684 26.380
## <none> 43.327 26.837
## - x4 1 1.8676 45.194 26.947
## - x10 1 2.1111 45.438 27.216
## - x17 1 2.5819 45.908 27.731
## - x5 1 7.6954 51.022 33.012
## - x3 1 29.4195 72.746 50.748
##
## Step: AIC=24.88
## y ~ x1 + x3 + x4 + x5 + x6 + x8 + x9 + x10 + x11 + x13 + x14 +
## x15 + x17 + x19 + x20
##
## Df Sum of Sq RSS AIC
## - x9 1 0.0561 43.418 22.943
## - x15 1 0.0611 43.423 22.949
## - x8 1 0.1377 43.500 23.037
## - x11 1 0.1883 43.550 23.095
## - x20 1 0.3496 43.712 23.280
## - x1 1 0.4835 43.846 23.433
## - x14 1 0.7525 44.115 23.738
## - x6 1 0.7779 44.140 23.767
## - x13 1 0.8252 44.187 23.821
## - x19 1 1.4585 44.821 24.532
## <none> 43.362 24.878
## - x4 1 1.8978 45.260 25.020
## - x10 1 2.0755 45.438 25.216
## - x17 1 2.5486 45.911 25.734
## - x5 1 7.6898 51.052 31.041
## - x3 1 30.7537 74.116 49.680
##
## Step: AIC=22.94
## y ~ x1 + x3 + x4 + x5 + x6 + x8 + x10 + x11 + x13 + x14 + x15 +
## x17 + x19 + x20
##
## Df Sum of Sq RSS AIC
## - x15 1 0.0518 43.470 21.003
## - x8 1 0.1738 43.592 21.143
## - x11 1 0.1947 43.613 21.167
## - x20 1 0.3358 43.754 21.328
## - x1 1 0.5825 44.001 21.609
## - x14 1 0.6995 44.118 21.742
## - x6 1 0.7287 44.147 21.775
## - x13 1 0.8339 44.252 21.894
## - x19 1 1.7204 45.139 22.886
## <none> 43.418 22.943
## - x4 1 1.8578 45.276 23.038
## - x10 1 2.0342 45.452 23.232
## - x17 1 2.5827 46.001 23.832
## - x5 1 7.8563 51.275 29.259
## - x3 1 31.0540 74.472 47.920
##
## Step: AIC=21
## y ~ x1 + x3 + x4 + x5 + x6 + x8 + x10 + x11 + x13 + x14 + x17 +
## x19 + x20
##
## Df Sum of Sq RSS AIC
## - x8 1 0.184 43.654 19.214
## - x11 1 0.198 43.668 19.230
## - x20 1 0.404 43.874 19.465
## - x1 1 0.654 44.124 19.749
## - x6 1 0.679 44.149 19.778
## - x14 1 0.690 44.160 19.790
## - x13 1 0.800 44.270 19.914
## - x19 1 1.716 45.186 20.938
## <none> 43.470 21.003
## - x4 1 1.910 45.380 21.152
## - x10 1 1.984 45.454 21.234
## - x17 1 2.531 46.001 21.832
## - x5 1 8.197 51.668 27.640
## - x3 1 31.851 75.321 46.487
##
## Step: AIC=19.21
## y ~ x1 + x3 + x4 + x5 + x6 + x10 + x11 + x13 + x14 + x17 + x19 +
## x20
##
## Df Sum of Sq RSS AIC
## - x11 1 0.271 43.926 17.524
## - x20 1 0.399 44.054 17.670
## - x6 1 0.670 44.325 17.976
## - x13 1 0.749 44.404 18.065
## - x1 1 0.768 44.423 18.087
## - x14 1 1.040 44.695 18.391
## <none> 43.654 19.214
## - x4 1 1.828 45.482 19.265
## - x19 1 1.889 45.544 19.333
## - x10 1 1.986 45.640 19.438
## - x17 1 2.512 46.166 20.011
## - x5 1 8.153 51.808 25.776
## - x3 1 33.960 77.614 45.986
##
## Step: AIC=17.52
## y ~ x1 + x3 + x4 + x5 + x6 + x10 + x13 + x14 + x17 + x19 + x20
##
## Df Sum of Sq RSS AIC
## - x20 1 0.264 44.190 15.824
## - x1 1 0.773 44.699 16.396
## - x14 1 0.912 44.838 16.551
## - x13 1 0.931 44.857 16.573
## - x6 1 1.045 44.971 16.699
## <none> 43.926 17.524
## - x19 1 1.895 45.821 17.636
## - x10 1 1.960 45.886 17.707
## - x4 1 2.020 45.946 17.772
## - x17 1 2.718 46.644 18.526
## - x5 1 8.581 52.507 24.446
## - x3 1 33.736 77.661 44.017
##
## Step: AIC=15.82
## y ~ x1 + x3 + x4 + x5 + x6 + x10 + x13 + x14 + x17 + x19
##
## Df Sum of Sq RSS AIC
## - x14 1 0.784 44.974 14.703
## - x1 1 0.828 45.018 14.752
## - x6 1 0.951 45.141 14.888
## - x13 1 1.124 45.314 15.080
## - x10 1 1.770 45.960 15.788
## - x4 1 1.780 45.970 15.798
## <none> 44.190 15.824
## - x19 1 2.050 46.240 16.091
## - x17 1 2.930 47.120 17.034
## - x5 1 8.767 52.957 22.873
## - x3 1 34.253 78.443 42.518
##
## Step: AIC=14.7
## y ~ x1 + x3 + x4 + x5 + x6 + x10 + x13 + x17 + x19
##
## Df Sum of Sq RSS AIC
## - x6 1 0.965 45.939 13.765
## - x1 1 1.146 46.120 13.962
## - x4 1 1.476 46.450 14.318
## - x13 1 1.682 46.657 14.540
## <none> 44.974 14.703
## - x19 1 2.214 47.188 15.106
## - x10 1 2.427 47.401 15.331
## - x17 1 3.404 48.378 16.351
## - x5 1 10.639 55.613 23.320
## - x3 1 35.684 80.658 41.910
##
## Step: AIC=13.76
## y ~ x1 + x3 + x4 + x5 + x10 + x13 + x17 + x19
##
## Df Sum of Sq RSS AIC
## - x1 1 0.916 46.855 12.752
## - x4 1 1.573 47.512 13.448
## - x10 1 1.794 47.734 13.681
## - x13 1 1.832 47.771 13.720
## <none> 45.939 13.765
## - x19 1 2.307 48.247 14.215
## - x17 1 2.853 48.793 14.778
## - x5 1 13.166 59.105 24.365
## - x3 1 36.703 82.642 41.125
##
## Step: AIC=12.75
## y ~ x3 + x4 + x5 + x10 + x13 + x17 + x19
##
## Df Sum of Sq RSS AIC
## - x13 1 1.223 48.079 12.041
## - x4 1 1.293 48.149 12.113
## - x10 1 1.568 48.423 12.397
## <none> 46.855 12.752
## - x19 1 2.072 48.927 12.915
## - x17 1 4.306 51.161 15.148
## - x5 1 12.554 59.409 22.621
## - x3 1 36.144 82.999 39.340
##
## Step: AIC=12.04
## y ~ x3 + x4 + x5 + x10 + x17 + x19
##
## Df Sum of Sq RSS AIC
## - x4 1 1.428 49.506 11.504
## - x10 1 1.868 49.946 11.946
## <none> 48.079 12.041
## - x19 1 2.174 50.252 12.252
## - x17 1 3.769 51.847 13.814
## - x5 1 12.160 60.238 21.314
## - x3 1 38.040 86.119 39.185
##
## Step: AIC=11.5
## y ~ x3 + x5 + x10 + x17 + x19
##
## Df Sum of Sq RSS AIC
## - x10 1 1.572 51.078 11.067
## - x19 1 1.976 51.482 11.461
## <none> 49.506 11.504
## - x17 1 4.252 53.759 13.624
## - x5 1 10.882 60.388 19.439
## - x3 1 38.822 88.328 38.452
##
## Step: AIC=11.07
## y ~ x3 + x5 + x17 + x19
##
## Df Sum of Sq RSS AIC
## <none> 51.078 11.067
## - x19 1 2.339 53.417 11.305
## - x17 1 5.248 56.326 13.957
## - x5 1 10.186 61.264 18.159
## - x3 1 41.916 92.994 39.026選択されたモデルの要約を表示します。
summary(mod_aic_min)
##
## Call:
## lm(formula = y ~ x3 + x5 + x17 + x19, data = d1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.1815 -0.6985 -0.0454 0.6641 2.7790
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.1184 0.1560 -0.759 0.45173
## x3 0.9619 0.1583 6.077 2.4e-07 ***
## x5 -0.4937 0.1648 -2.996 0.00444 **
## x17 0.3253 0.1513 2.150 0.03694 *
## x19 0.2103 0.1465 1.435 0.15809
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.065 on 45 degrees of freedom
## Multiple R-squared: 0.5142, Adjusted R-squared: 0.471
## F-statistic: 11.91 on 4 and 45 DF, p-value: 1.11e-06x3, x5, x17が有意になっていますが、実際に関連があるのはx3だけです。x5とx17は、ほんとうは関係はないけれども、このサンプルでたまたま有意になっただけです。
フルモデルで線形回帰
普通にフルモデルで線形回帰したときに、同じ説明変数でどのようになるかを確認します。
selected_x <- names(coef(mod_aic_min))[-1] |>
substring(2) |>
as.numeric()
summary(fit_lm)$coefficients[selected_x + 1, ]
## Estimate Std. Error t value Pr(>|t|)
## x3 0.9086697 0.2088203 4.3514427 0.0001529615
## x5 -0.4947387 0.2281541 -2.1684413 0.0384690079
## x17 0.2625604 0.2121741 1.2374761 0.2258367674
## x19 0.1805438 0.1932606 0.9341985 0.3579154706前の結果と比較すると、x17が有意ではなくなりました(くりかえしますが、実際は関係のない変数です)。その他の説明変数でもp値が大きくなっています。
検証用データでの線形回帰
検証用データでも同様にやってみます。
test_lm <- lm(f, data = d2)
summary(test_lm)$coefficients[selected_x + 1, ]
## Estimate Std. Error t value Pr(>|t|)
## x3 0.7940754 0.2152929 3.68834960 0.0009258005
## x5 -0.0123052 0.1532589 -0.08029024 0.9365579532
## x17 0.1335787 0.2343590 0.56997477 0.5730843759
## x19 0.2561039 0.2069814 1.23732815 0.2258908555当然ながら、x3以外は有意ではありません。生成されたサンプルによっては有意になることもあるでしょうが、ほんとうはx3以外は無関係の変数です。
シミュレーション
1回だけではよくわからないので、繰り返しシミュレーションしてみます。
モデル選択後の検定
まずはシミュレーション用の関数を定義します。選択されたモデルに含まれる説明変数で、モデル選択後に有意水準5%で有意になったものの番号を返します。
sim_modsel <- function(N = 100, num_x = 20) {
x <- rnorm(N * num_x, 0, 1)
d <- matrix(x, ncol = num_x) |>
data.frame()
colnames(d) <- paste0("x", 1:num_x)
d$y <- d$x3 + rnorm(N, 0, 1)
f <- reformulate(paste0("x", 1:num_x), response = "y")
fit <- lm(formula = f, data = d)
coef_aic_min <- stepAIC(fit, trace = 0) |>
summary() |>
coef()
sig_coef <- (coef_aic_min[-1, "Pr(>|t|)"] < 0.05) # omit intercept
names(sig_coef)[sig_coef] |>
substring(2) |>
as.numeric()
}まず、N=50のときです。parallelsパッケージのmclapply関数で並列化しています(WindowsではparLapply関数を使う必要があります)。
set.seed(123)
R <- 2000 # replications
result_modsel1 <- mclapply(seq_len(R),
function(i) sim_modsel(N = 50, num_x = 20)) |>
unlist() |>
as.factor()
data.frame(x = result_modsel1) |>
ggplot() +
geom_bar(aes(x = x)) +
geom_hline(aes(yintercept = R * 0.05), color = "red") +
ylim(0, R)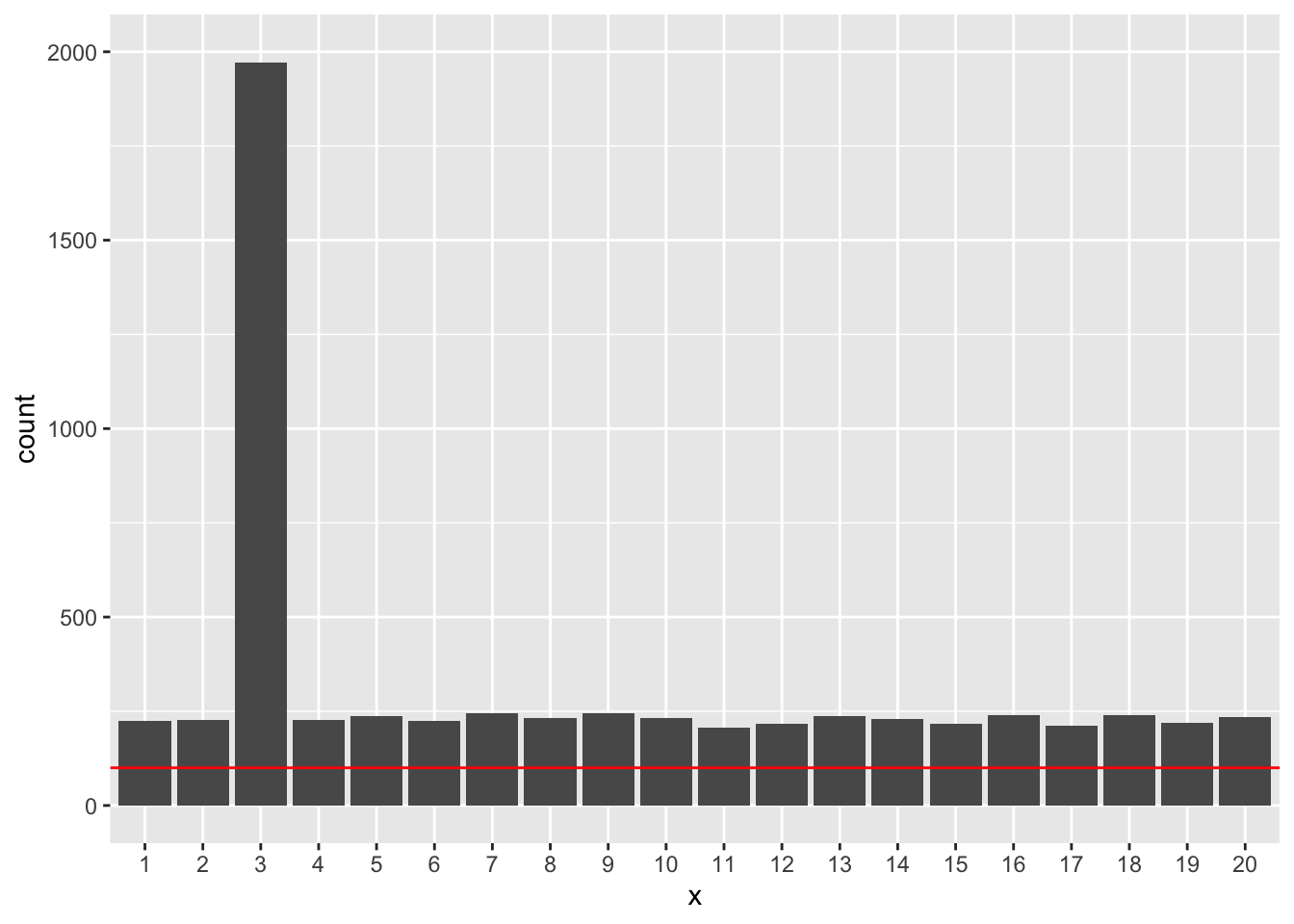
赤線はcount=100の線です。2000回の繰り返しですので、有意水準5%なら、関係がないのに有意になる回数は2000×0.05=100回くらいのはずです。しかし、この場合、実際に関係のあるx3以外の説明変数でもすべて100を超えてしまっています。
次にN=500として、やってみます。
result_modsel2 <- mclapply(seq_len(R),
function(i) sim_modsel(N = 500, num_x = 20)) |>
unlist() |>
as.factor()
data.frame(x = result_modsel2) |>
ggplot() +
geom_bar(aes(x = x)) +
geom_hline(aes(yintercept = R * 0.05), color = "red") +
ylim(0, R)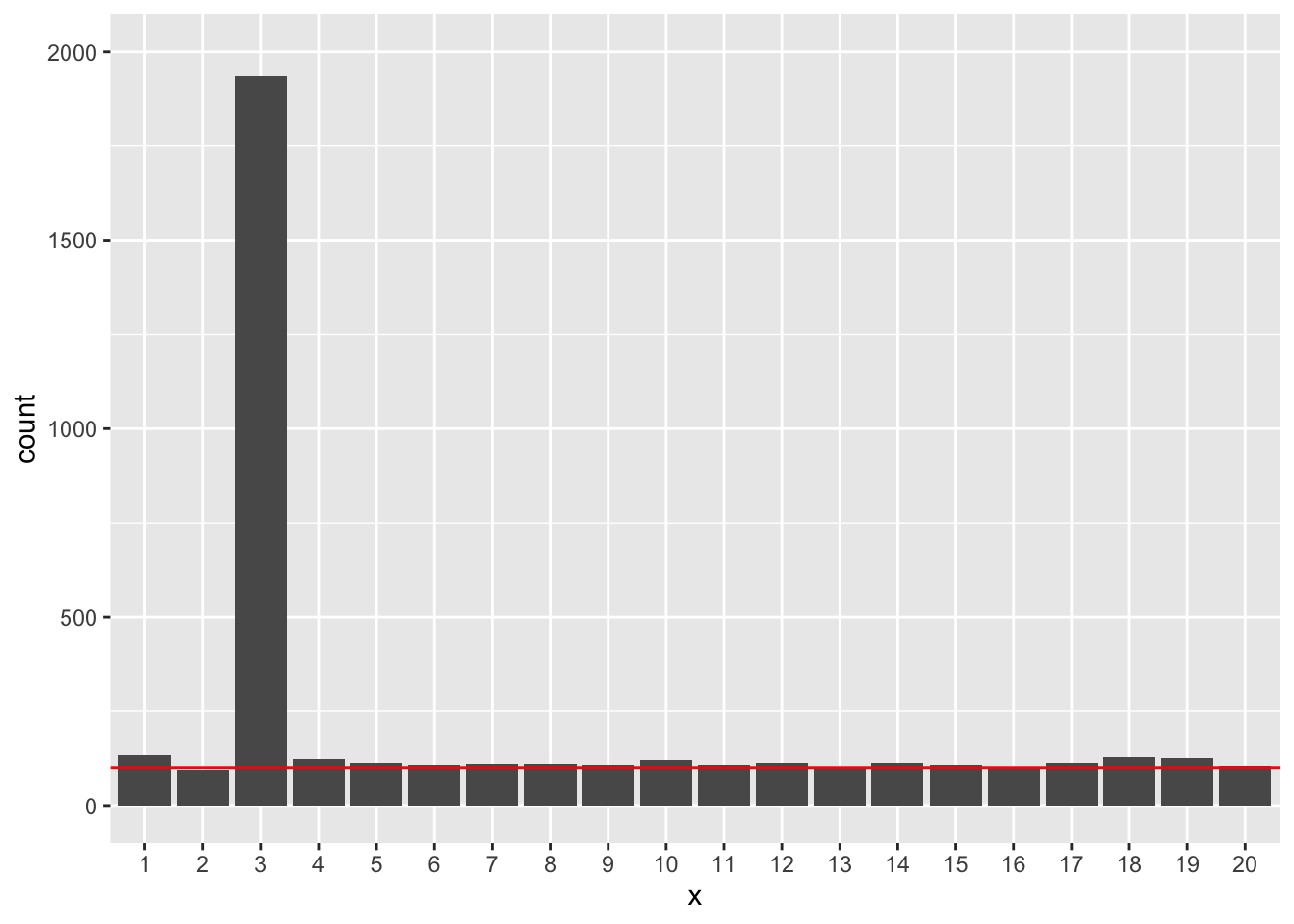
N=500のときは、x3以外の説明変数が有意になる回数がどれも5%くらいに収まるようになりました。
では、サンプルサイズが大きければいつでもうまくいくかというとそうでもありません(実例2でしめします)。
フルモデルでの線形回帰
モデル選択をおこなわずに、フルモデルで線形回帰した場合はどうなるかやってみます。
まずはシミュレーション用の関数定義です。有意になった説明変数の番号を返します。
sim_lm <- function(N = 100, num_x = 20) {
x <- rnorm(N * num_x, 0, 1)
d <- matrix(x, ncol = num_x) |>
data.frame()
colnames(d) <- paste0("x", 1:num_x)
d$y <- d$x3 + rnorm(N, 0, 1)
f <- reformulate(paste0("x", 1:num_x), response = "y")
fit <- lm(formula = f, data = d)
coef_lm <- fit |>
summary() |>
coef()
sig_coef <- (coef_lm[-1, "Pr(>|t|)"] < 0.05) # omit intercept
names(sig_coef)[sig_coef] |>
substring(2) |>
as.numeric()
}N=50の場合です。
result_lm1 <- mclapply(seq_len(R),
function(i) sim_lm(N = 50, num_x = 20)) |>
unlist() |>
as.factor()
data.frame(x = result_lm1) |>
ggplot() +
geom_bar(aes(x = x)) +
geom_hline(aes(yintercept = R * 0.05), color = "red") +
ylim(0, R)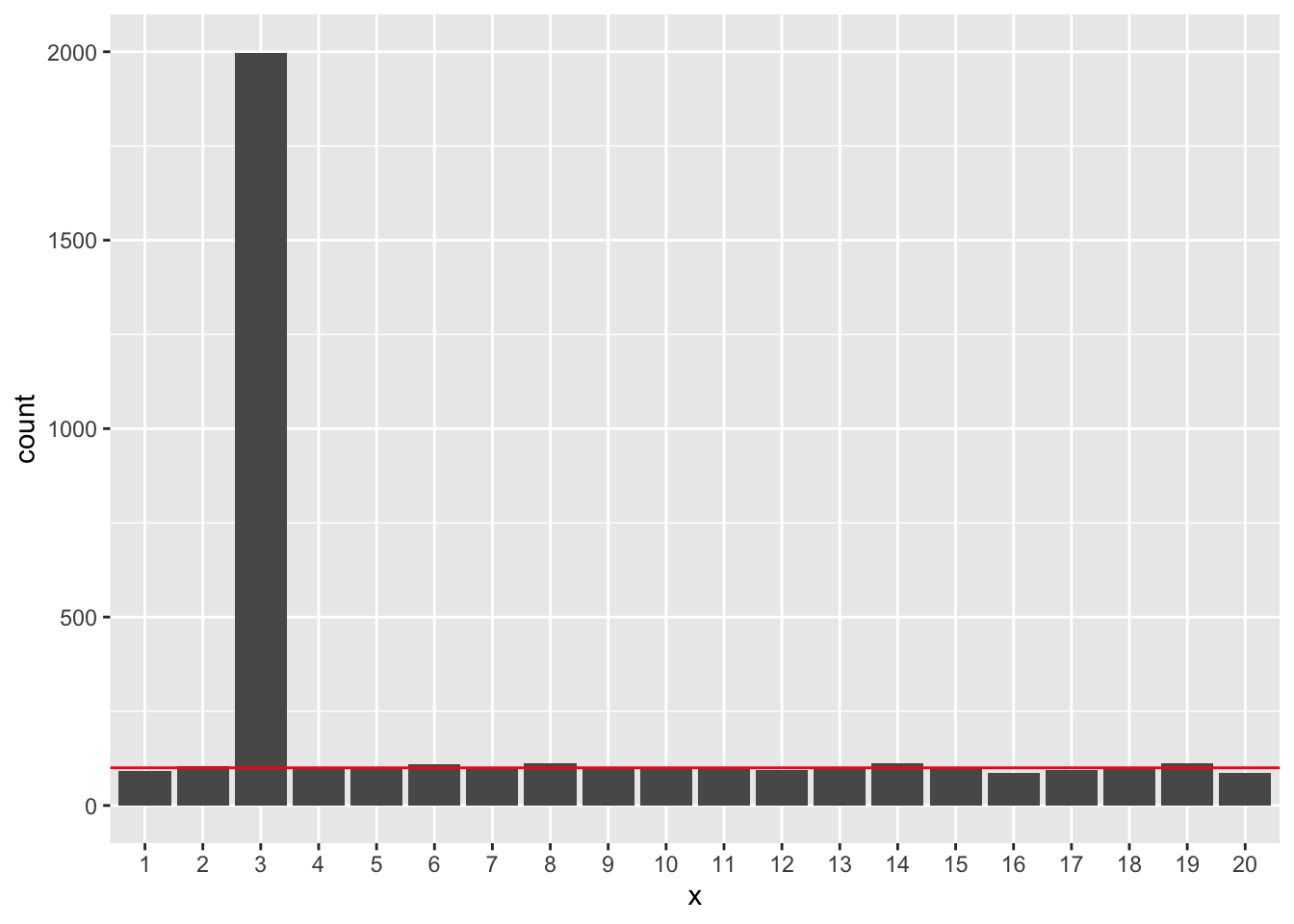
N=500の場合です。
result_lm2 <- mclapply(seq_len(R),
function(i) sim_lm(N = 500, num_x = 20)) |>
unlist() |>
as.factor()
data.frame(x = result_lm2) |>
ggplot() +
geom_bar(aes(x = x)) +
geom_hline(aes(yintercept = R * 0.05), color = "red") +
ylim(0, R)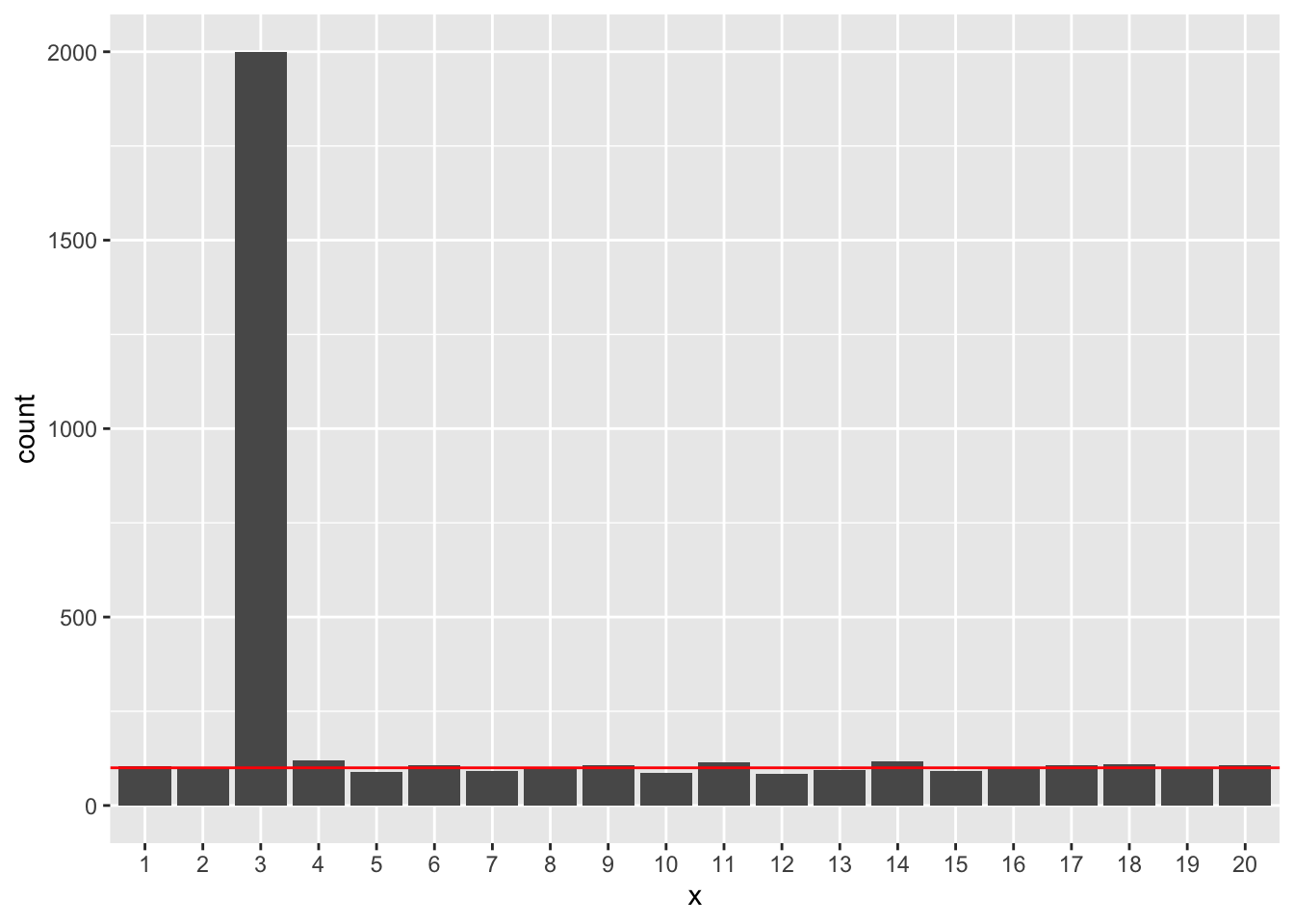
いずれの場合でも、x3以外の説明変数が有意になるのは、正しく5%程度となっていました。
実例2
以下のようなデータを想定します。目的変数yはx1にのみ依存します。
\[ x_1 \sim \mathrm{Normal}(0, 1), \quad x_2 \sim \mathrm{Normal}(0, 1) \]
\[ y = x_1 + \epsilon, \quad \epsilon \sim \mathrm{Normal}(0, 1) \]
以下の2つのモデルで、AICによりモデル選択をおこないます。
y ~ x1y ~ x1 + x2
シミュレーション
関数を定義します。選択されたモデルの番号と当てはめ結果を返します。
sim2 <- function(N = 100) {
x1 <- rnorm(N, 0, 1)
x2 <- rnorm(N, 0, 1)
y <- 1.0 * x1 + rnorm(N, 0, 1)
d <- data.frame(x1 = x1, x2 = x2, y = y)
mod <- list()
mod[[1]] <- lm(y ~ x1, data = d)
mod[[2]] <- lm(y ~ x1 + x2, data = d)
sel <- ifelse(AIC(mod[[1]]) < AIC(mod[[2]]), 1, 2)
list(model = sel, fit = mod[[sel]])
}N=20のとき
サンプルサイズが20のとき、モデル1と2のどちらが選択されるかを計算します。
シミュレーションの繰り返し回数は2000回とします。
set.seed(123)
R <- 2000
results1 <- lapply(seq_len(R), function(i) sim2(N = 20))
selected_model1 <- sapply(seq_len(R), function(i) results1[[i]]$model)
as.factor(selected_model1) |>
table()
##
## 1 2
## 1623 377モデル1が多く選択されますが。モデル2が選択される場合も377回ありました。
モデル2が選択された場合に、x2の係数が有意水準5%で有意になる割合を求めます。
p1_mod2_x2 <- sapply(seq_len(R)[selected_model1 == 2],
function(i) {
coef(summary(results1[[i]]$fit))["x2", "Pr(>|t|)"]
})
sum(p1_mod2_x2 < 0.05) / length(p1_mod2_x2)
## [1] 0.2864721データを生成したモデルにはx2は含まれませんから、誤って有意になる割合は5%程度になる必要がありますが、結果は5%を大きく超えてしまっています。
N=500のとき
results2 <- lapply(seq_len(R), function(i) sim2(N = 500))
selected_model2 <- sapply(seq_len(R), function(i) results2[[i]]$model)
as.factor(selected_model2) |>
table()
##
## 1 2
## 1688 312やはり、モデル2が選択される場合が少なからずありました。
モデル2が選択された場合に、x2の係数が有意水準5%で有意になる割合を求めます。
p2_mod2_x2 <- sapply(seq_len(R)[selected_model2 == 2],
function(i) {
coef(summary(results2[[i]]$fit))["x2", "Pr(>|t|)"]
})
sum(p2_mod2_x2 < 0.05) / length(p2_mod2_x2)
## [1] 0.349359N=20のときと同様、結果は5%を大きく超えてしまっています。むしろ、N=20のときよりもさらに値が大きくなりました。
モデル2が選択された場合の、x2の係数のヒストグラムを表示します。
coef_mod2_x2 <- sapply(seq_len(R)[selected_model2 == 2],
function(i) {
coef(results2[[i]]$fit)["x2"]
})
data.frame(x1 = coef_mod2_x2) |>
ggplot() +
geom_histogram(aes(x = x1), binwidth = 0.02)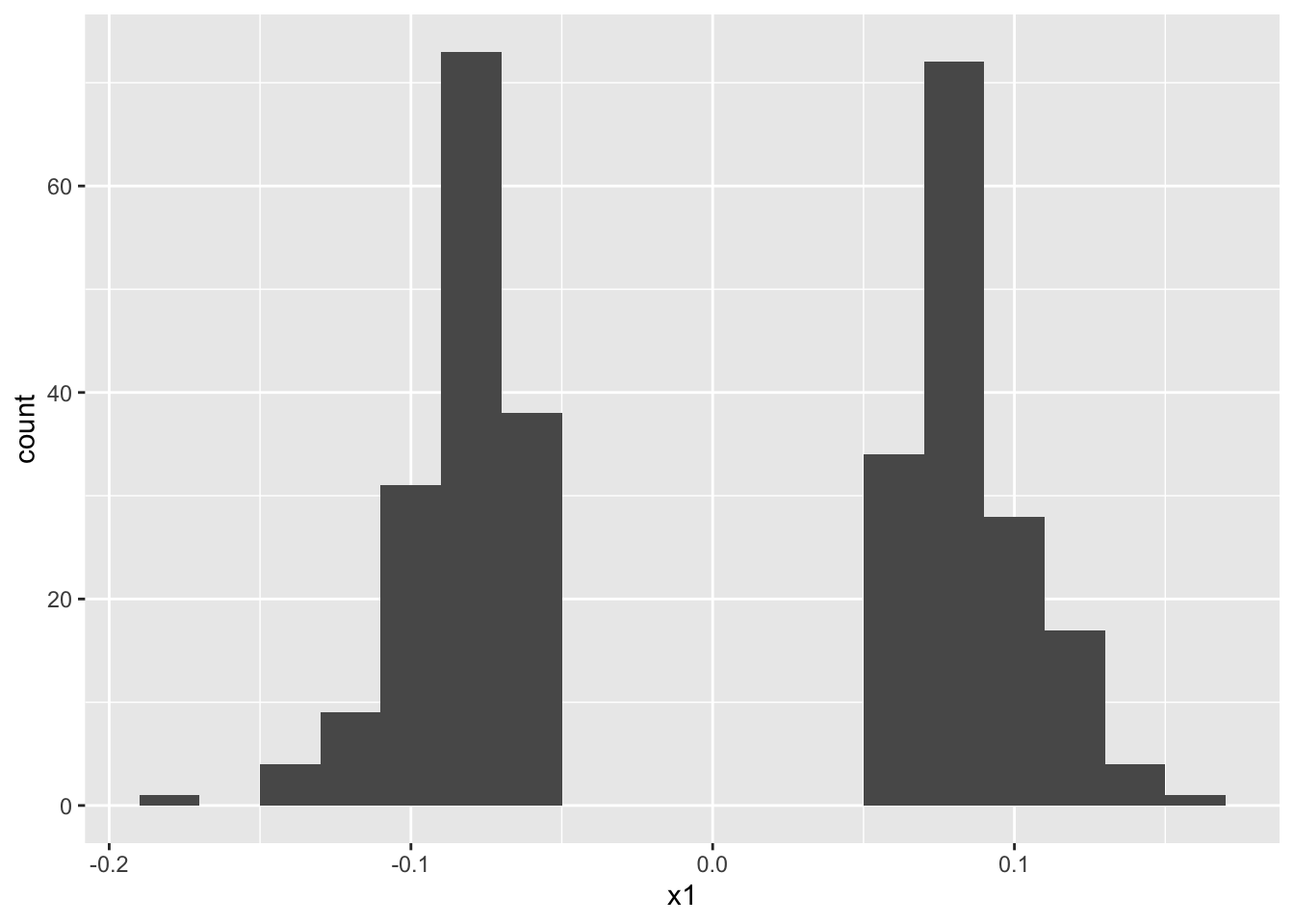
0のあたりがごっそりと抜けた、特異な分布となっています。
結論として、モデル2が選択されたという条件付きでは(その場合も少なからず発生する)、本来無関係なx2が有意になる割合が設定した有意水準を超え、係数の推定値の分布も特異なものになります。これはサンプルサイズを大きくしても解決されません。
おわりに
(AICに限らず)モデル選択後の推定についての統計学的な解説は Leeb and Pötscher (2005) などを参照してください。
また、モデル選択後の推定を正しくおこなうためのRパッケージとして、selectiveInferenceパッケージがあります。
しかしそもそもAICは、「正しいモデル」(データを生成したモデル)ではなく、もっとも予測性能の高いモデルを選ぶものです(久保 (2012) p.90–91, 粕谷 (2015))。AICで選択されたモデルに含まれる説明変数が、実際に目的変数に何らかの効果を及ぼしているかはわかりません。
回帰分析にあたっては、その目的が
- 目的変数と説明変数の関係の記述,
- 説明変数による目的変数の予測
- 目的変数に対する説明変数の介入効果の推定
のいずれであるかを意識するようにする必要があるでしょう(竹下ほか 2022)。
参考文献
- 粕谷英一 (2015) 生態学におけるAICの誤用 : AICは正しいモデルを選ぶためのものではないので正しいモデルを選ばない. 日本生態学会誌 65: 179-185. doi:10.18960/seitai.65.2_179
- 久保拓弥 (2012) データ解析のための統計モデリング入門—一般化線形モデル・階層ベイズモデル・MCMC—. 岩波書店
- Leeb H., Pötscher B.M. (2005) Model selection and inference: Facts and fiction. Econometric Theory, 21(1):21–59. doi:10.1017/S0266466605050036
- 竹下和貴・林岳彦・横溝裕行 (2022) 哺乳類研究における非実験データセットに対する回帰分析の適用について. 哺乳類科学 62:69–79. doi:10.11238/mammalianscience.62.69