回帰分析の残差に自己相関がないかを検定する手法としてDurbin-Watson検定があります。RではcarパッケージのdurbinWatsonTest関数が利用可能です。
はじめに
自己相関のある時系列データに対して、何も考えずに時間を説明変数として、通常の線形回帰モデルをあてはめると、「有意」になる確率が、設定した有意水準を超えることがあるというのは、わりとよくいわれていることだと思います。
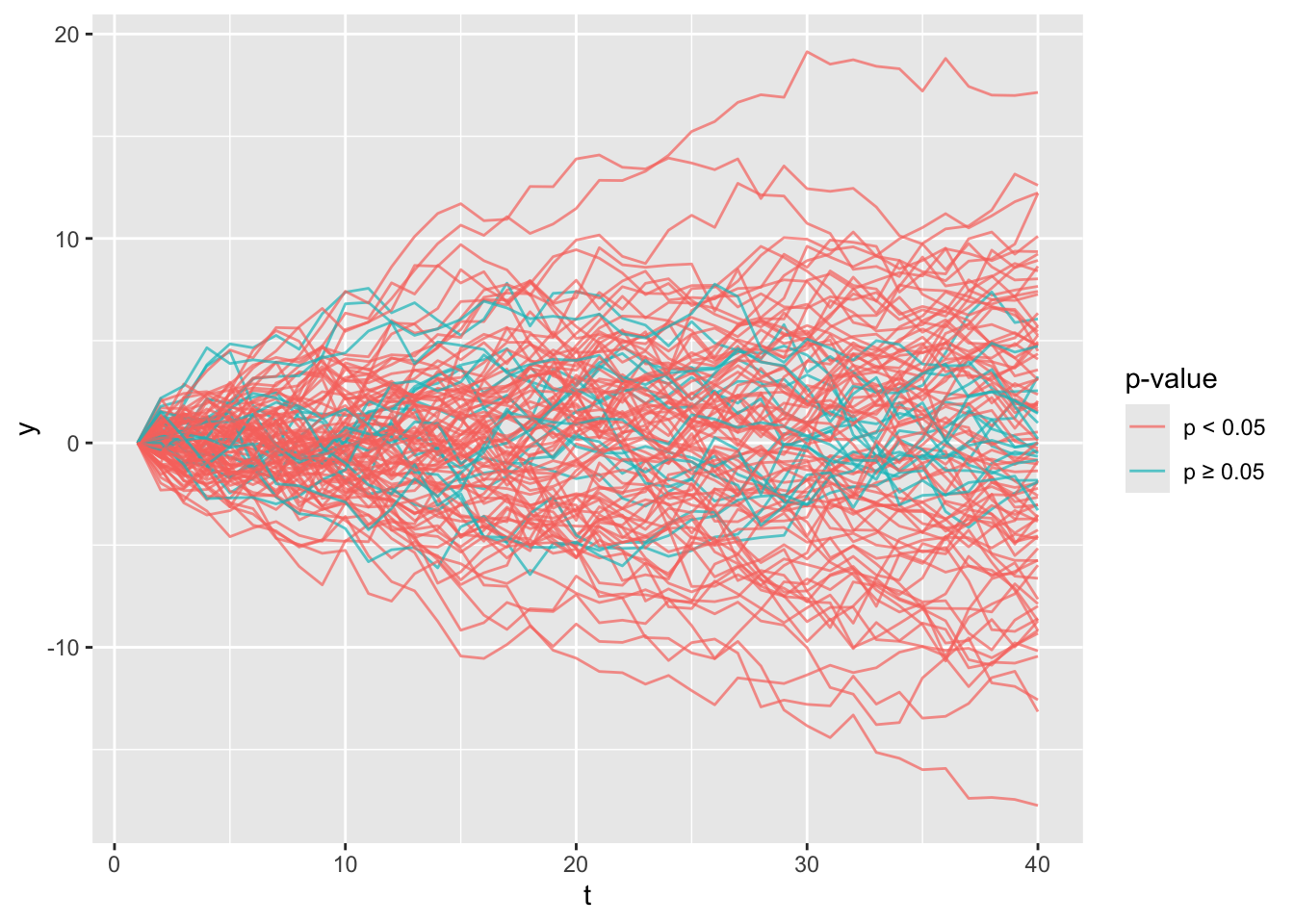
以下はその例です。0から始まるランダムウォークで時系列データを生成し、時間を説明変数として通常の線形回帰モデルをあてはめ、p値を計算する、ということをN回(この例では100回)くりかえします。
library(ggplot2)
set.seed(123)
N <- 100 # number of replications
Nt <- 40 # length of the time series
y <- matrix(0, ncol = N, nrow = Nt) # prepare response variable
for (t in 2:Nt) {
y[t, ] <- y[t - 1, ] + rnorm(N, 0, 1) # random walk
}
t <- seq_len(Nt) # time
p <- sapply(seq_len(N), function(n) { # calculate p-values
coef <- lm(y[, n] ~ t) |>
summary() |>
coef()
coef["t", "Pr(>|t|)"]})
data.frame(t = rep(t, N),
y = c(y),
g = rep(1:N, each = Nt),
p = rep(ifelse(p < 0.05, "p < 0.05", "p ≥ 0.05"),
each = Nt)) |>
ggplot() +
geom_line(aes(x = t, y = y, group = g, colour = p),
linewidth = 0.5, alpha = 0.7) +
scale_colour_discrete(name = "p-value")
p<0.05の場合は赤い線、p≥0.05の場合は青い線で描画しています。見てわかるように、赤い線の方が多くなっていますが、元のデータはランダムウォークで生成したものです。
割合を計算してみます。
sum(p < 0.05) / N
## [1] 0.83
有意水準5%にもかかわらず、83%が「有意」となっています。
Durbin-Watson検定
では、ランダムウォークで生成させた曲線に、時間を説明変数とした線形回帰モデルをあてはめた場合の残差に自己相関があるかどうか、Durbin-Watson検定を適用してみます。
まずはデータを生成します。
library(car)
## 要求されたパッケージ carData をロード中です
set.seed(1234)
Nt <- 40
y <- rep(0, Nt)
for (t in 2:Nt) {
y[t] <- y[t - 1] + rnorm(1, 0, 1)
}
t <- seq_len(Nt)
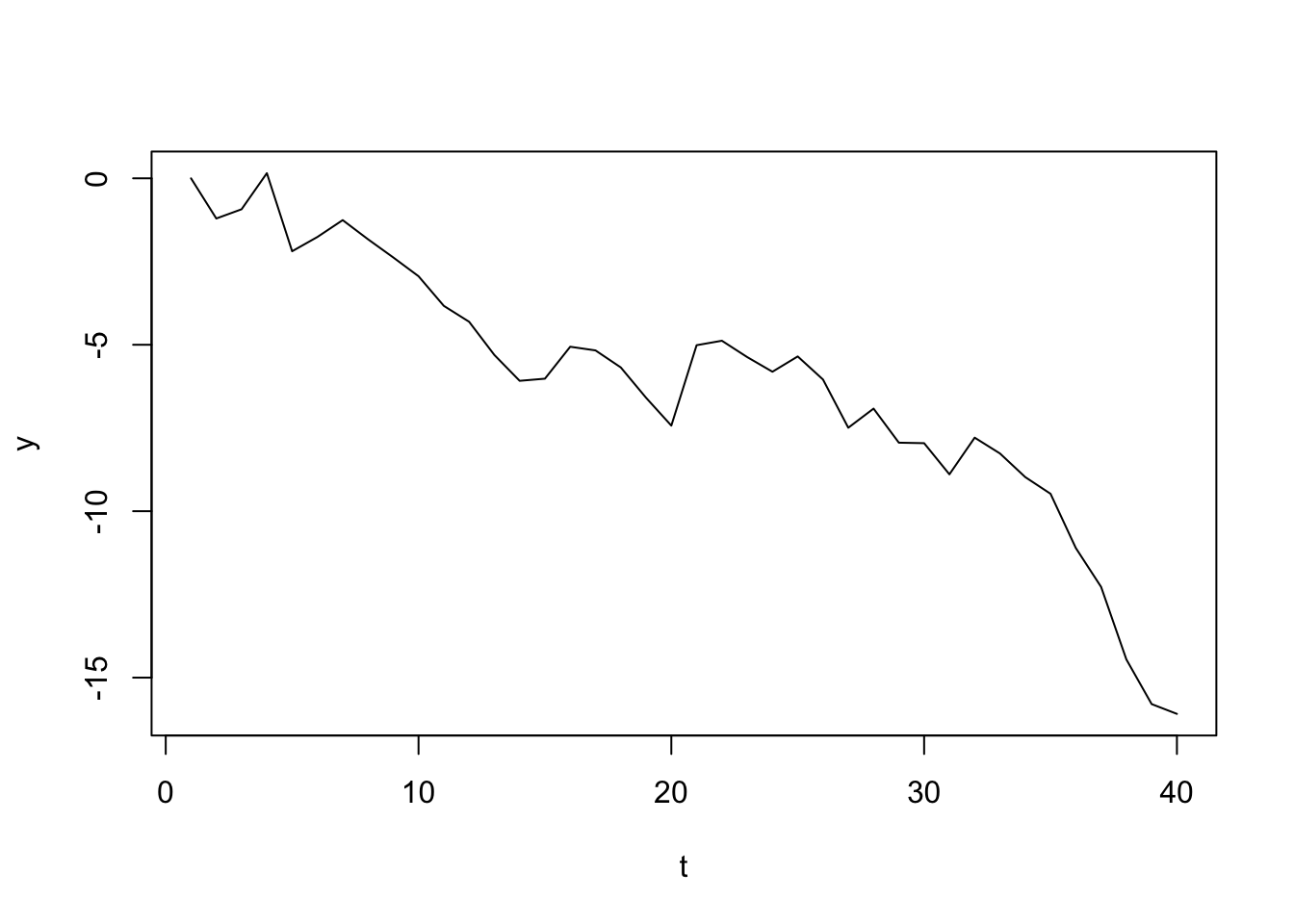
plot(t, y, type = "l")
lm関数で、線形回帰モデルをあてはめます。
lm1 <- lm(y ~ t)
summary(lm1)
##
## Call:
## lm(formula = y ~ t)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.8370 -0.8890 -0.0386 1.2393 2.2064
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.30034 0.49091 0.612 0.544
## t -0.31430 0.02087 -15.063 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.523 on 38 degrees of freedom
## Multiple R-squared: 0.8565, Adjusted R-squared: 0.8528
## F-statistic: 226.9 on 1 and 38 DF, p-value: < 2.2e-16
時間tの係数の推定値は-0.3143で、「有意」となりました。しかしランダムウォークで生成させたデータなので、もっと大きなtの値に対してもyの値が減少するという保証はまったくありません。
横軸を時間tとして、残差をプロットします。
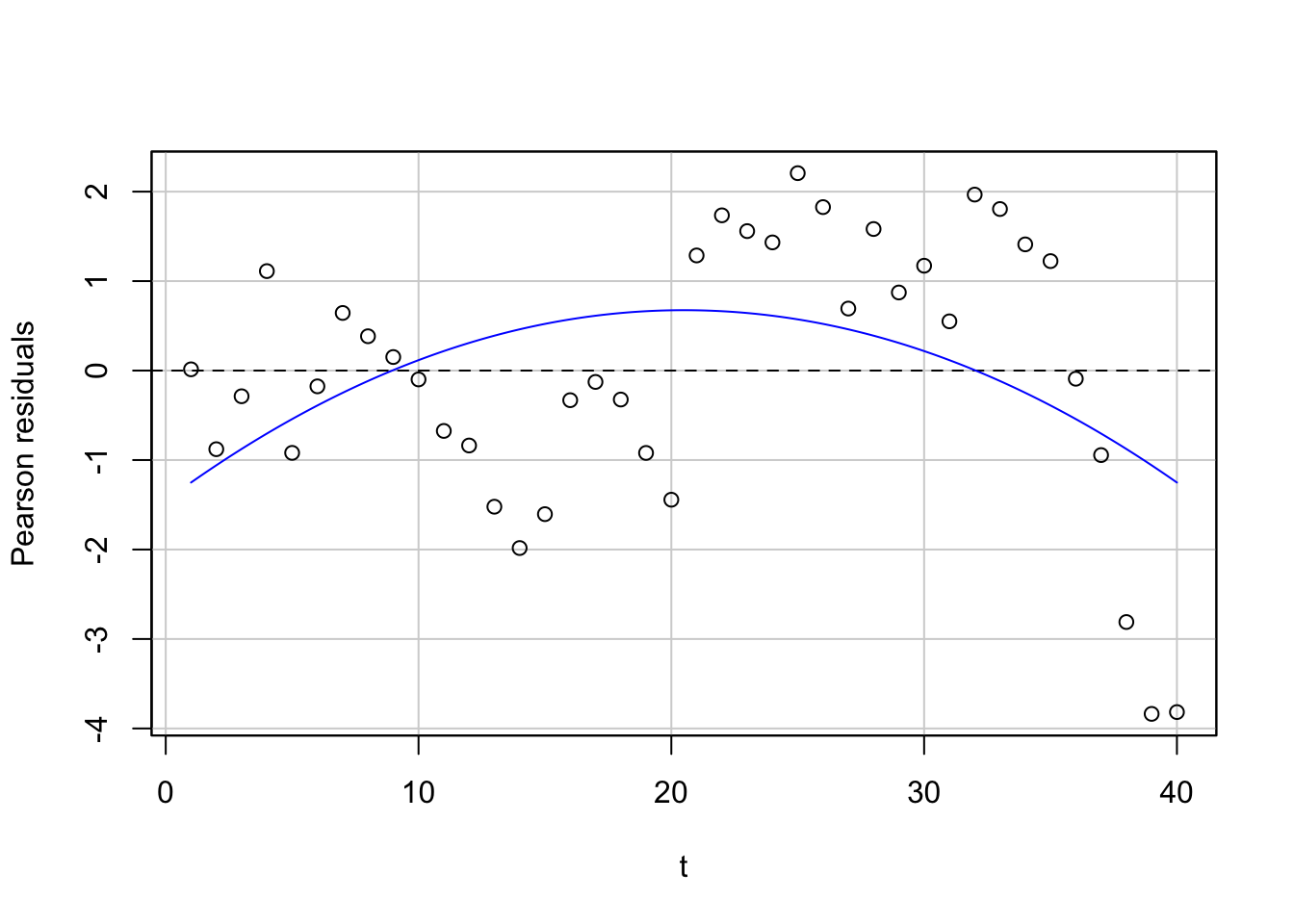
residualPlot(lm1, variable = "t")
残差がわりと固まっていて、自己相関がありそうに見えます。
Durbin-Watson検定を適用します。
durbinWatsonTest(lm1)
## lag Autocorrelation D-W Statistic p-value
## 1 0.7310166 0.3727528 0
## Alternative hypothesis: rho != 0
Durbin-Watson統計量は、正の自己相関があるときに0に近い値、負の自己相関があるときに4に近い値、自己相関がないときに2となります。この場合は0.3727528と、0に近い値となりました。自己相関がないことを帰無仮説とした検定ではp値が0となり、帰無仮説は棄却されました。
自己相関がないとき
つぎに、自己相関のない場合はどうかみてみます。まずはデータを生成します。独立したノイズが加わったデータです。
set.seed(1234)
x <- seq_len(Nt)
y2 <- -0.5 * x + rnorm(Nt, 0, 1)
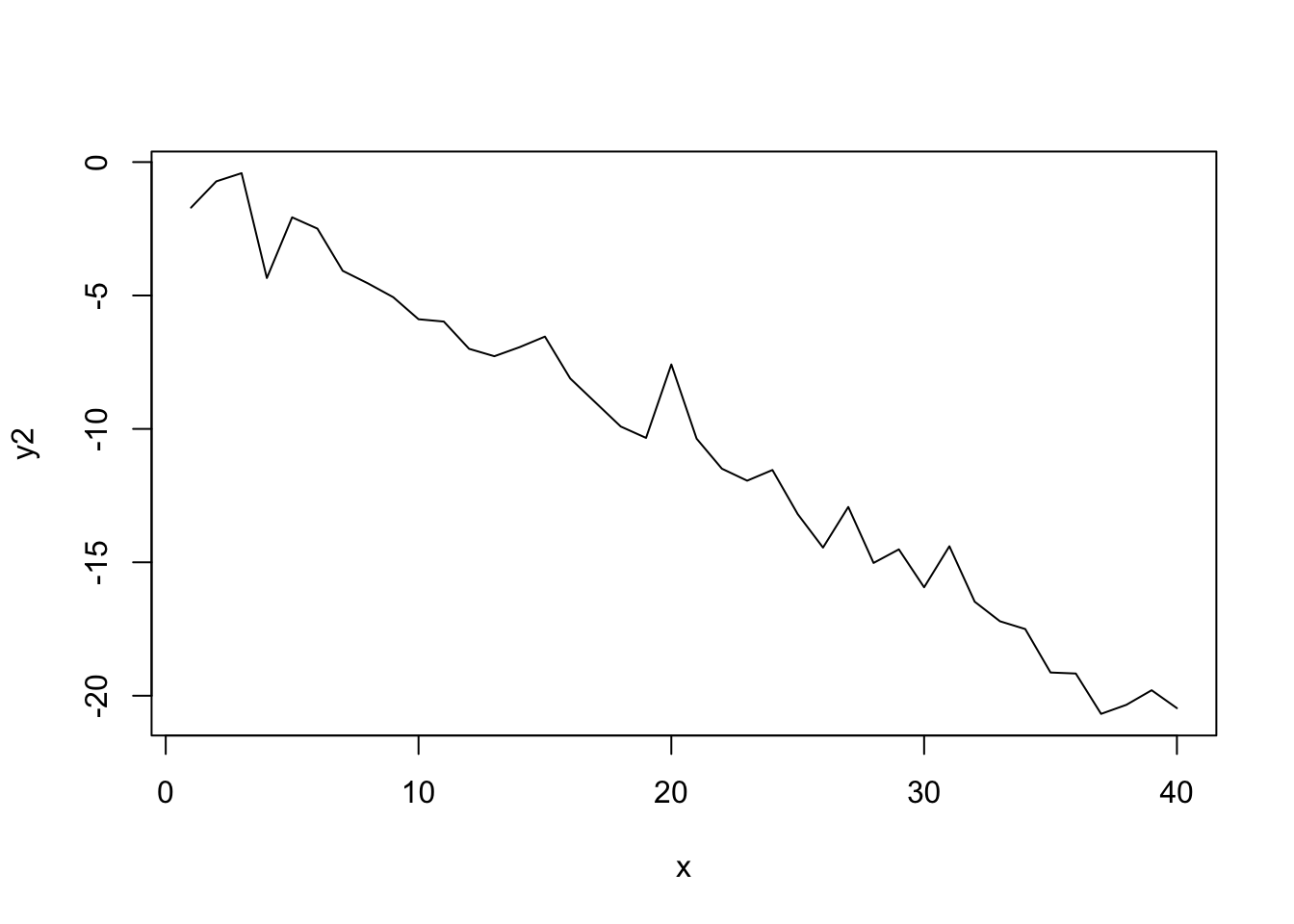
plot(x, y2, type = "l")
線形回帰の結果です。
lm2 <- lm(y2 ~ x)
summary(lm2)
##
## Call:
## lm(formula = y2 ~ x)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.1705 -0.5084 -0.1313 0.4482 2.8225
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.11732 0.29285 -0.401 0.691
## x -0.51447 0.01245 -41.330 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9088 on 38 degrees of freedom
## Multiple R-squared: 0.9782, Adjusted R-squared: 0.9777
## F-statistic: 1708 on 1 and 38 DF, p-value: < 2.2e-16
残差を見てみます。
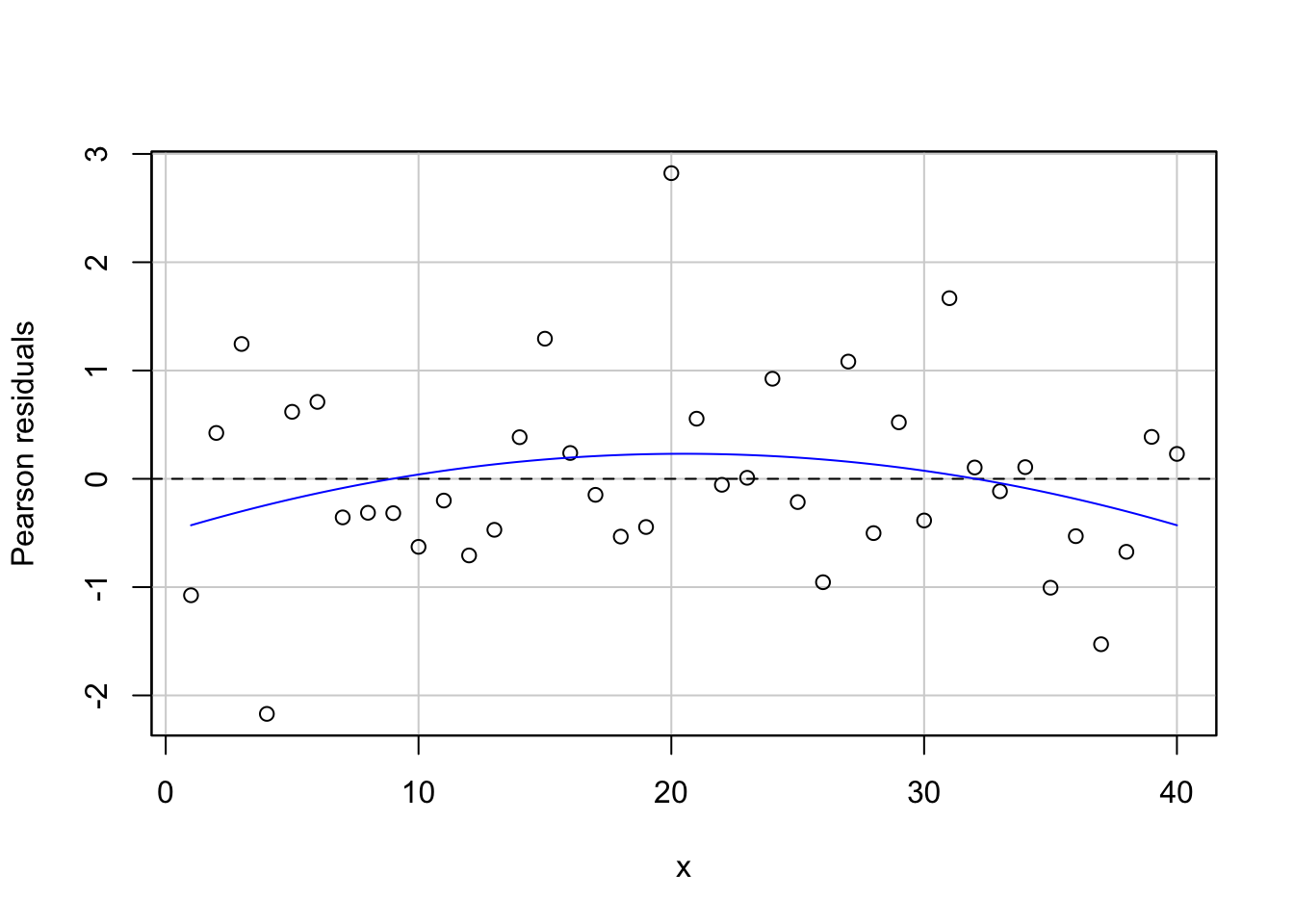
residualPlot(lm2, variable = "x")
残差は、偏りなくばらついているようです。
Durbin-Watson検定を適用します。
durbinWatsonTest(lm2)
## lag Autocorrelation D-W Statistic p-value
## 1 -0.06419093 2.089853 0.888
## Alternative hypothesis: rho != 0
Durbin-Watson統計量は2.0898532と、2に近い値となりました。また、自己相関がないことを帰無仮説とした検定では、帰無仮説は棄却されませんでした。