library(dlm)
library(ggplot2)
##
## 次のパッケージを付け加えます: 'ggplot2'
## 以下のオブジェクトは 'package:dlm' からマスクされています:
##
## %+%岩波データサイエンス Vol.6に書いた記事「Rによる状態空間モデリング—dlmとKFASを用いて—」のうち、dlmによる季節調整モデルの解析を(ちょっとだけ変えて)やりなおしてみました。元の記事の方がより詳細に書いてありますので、興味のある方はそちらも参照いただけると幸いです。
準備
パッケージ
dlmパッケージとggplot2パッケージを読み込みます。
データ
データは、岩波データサイエンスVol.1の松浦さんの記事で使用されたものを利用します。
data_url <- "https://raw.githubusercontent.com/iwanami-datascience/vol1/master/matsuura/example2/input/data-season.txt"
data <- read.csv(data_url)
data$Time <- seq_along(data$Y)まずはプロットしてデータを確認します。
p <- ggplot(data) +
geom_line(aes(x = Time, y = Y))
print(p)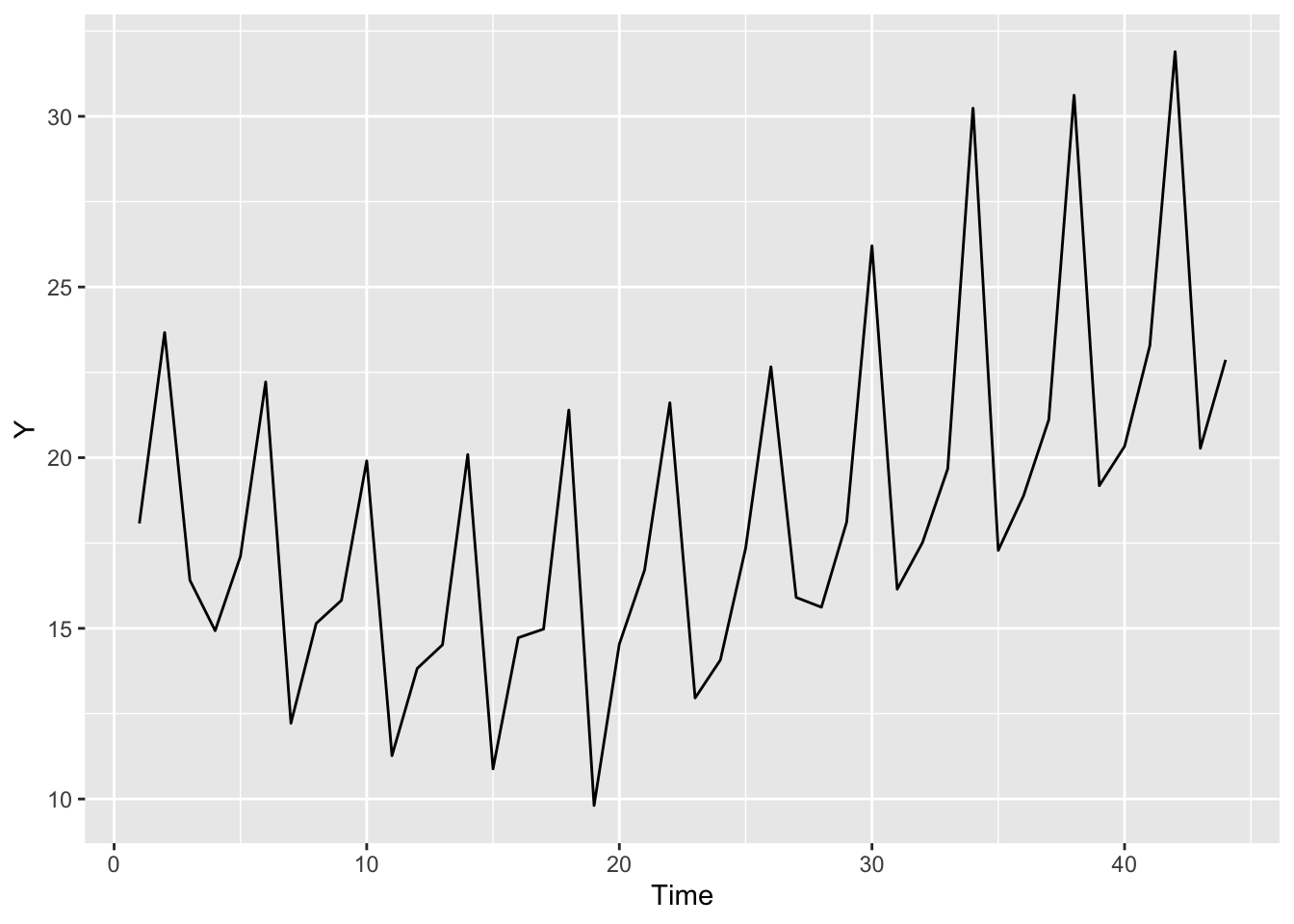
dlmによる解析
モデル
まずはモデルの構築です。build_fun関数でモデルを作成していきます。
引数のparは、あとでdlmMLE関数で最尤推定するときに、optim関数に渡されるパラメータです。ここでは、観測モデルの分散(V)と、システムモデルの分散(W)となるようにしています。
関数中のmodにモデルを格納します。dlmModPolyは多項モデルで、order=2でトレンドモデルになります。岩波データサイエンスVol.6の記事ではorder=1でローカルレベルモデルとしていましたが、今回はトレンドモデルとしました(ただし、結果はほとんど変わりませんでした)。これにdlmModSeasで季節調整項(周期4)を加えています。
V(mod)は観測モデルの分散です。Wの対角成分のうち1番目は水準成分の分散、2番目は傾き成分の分散、3番目は季節調整成分の分散です。これらを最尤推定するのでpar引数のそれぞれの要素を与えています。
m0(mod)は、初期状態の期待値です。このほか、C0で初期状態の分散共分散行列を指定するのですが、今回は省略して既定値を使用しています。
build_fun <- function(par) {
mod <- dlmModPoly(order = 2) +
dlmModSeas(frequency = 4)
V(mod) <- exp(par[1])
diag(W(mod))[1:3] <- c(exp(par[2:4]))
m0(mod) <- c(20, 0, 0, 0, 0)
return(mod)
}MLE
dlmMLE関数でパラメータを最尤推定します。最尤推定値を引数としてbuild_fun関数に与えて、最終的なモデルとしています。
mle <- dlmMLE(data$Y, parm = rep(0, 4),
build = build_fun)
mod <- build_fun(mle$par)平滑化
dlmSmooth関数で平滑化をおこないます。dropFirst(smo$s)では初期値を捨て、その後1番目の列の水準成分を取り出しています。平滑化した値を赤い線でプロットに加えました。
smo <- dlmSmooth(data$Y, mod)
lev <- dropFirst(smo$s)[, 1]
Smo <- data.frame(Time = data$Time, Level = lev)
p +
geom_line(data = Smo, aes(x = Time, y = Level), color = "red")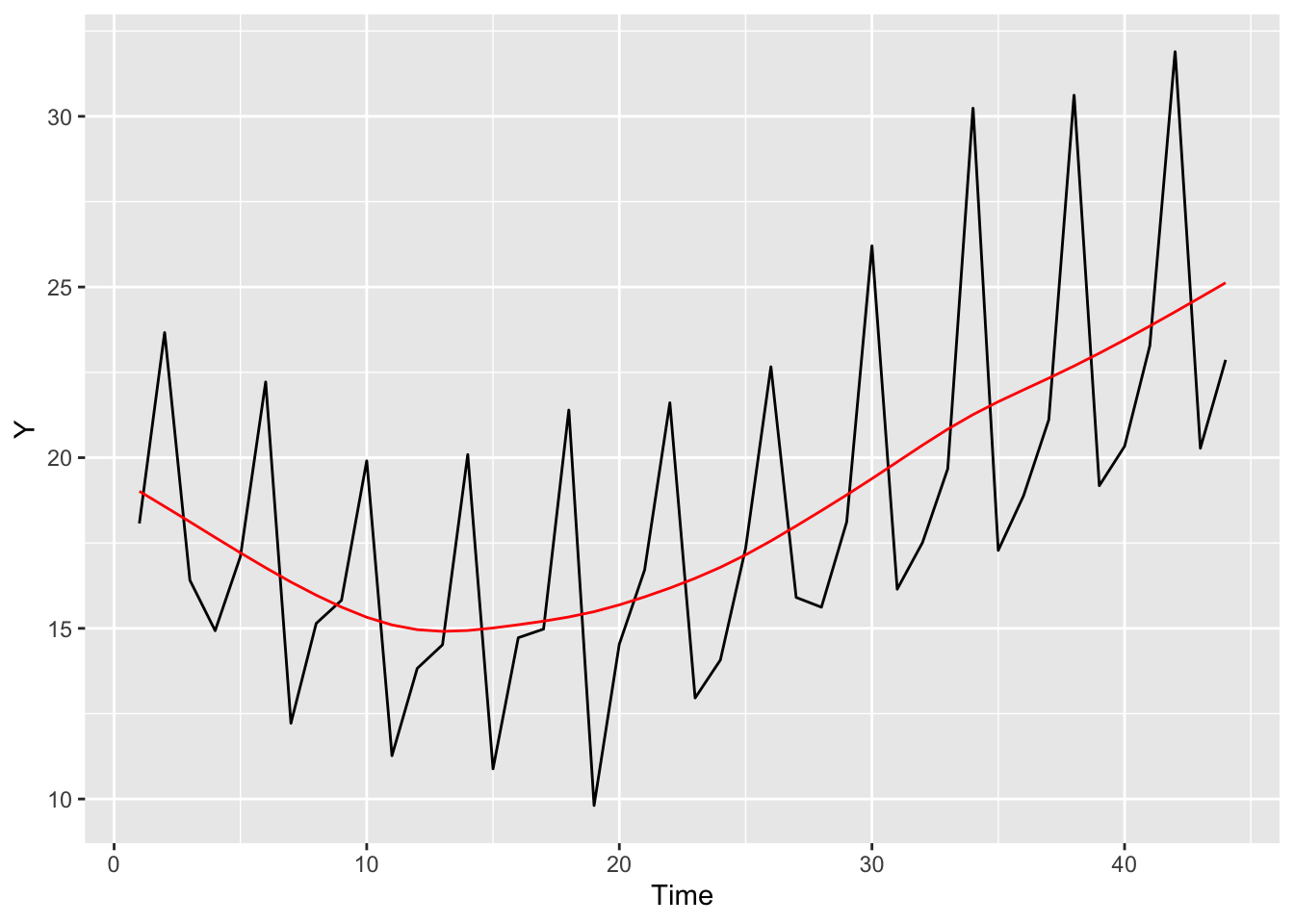
予測
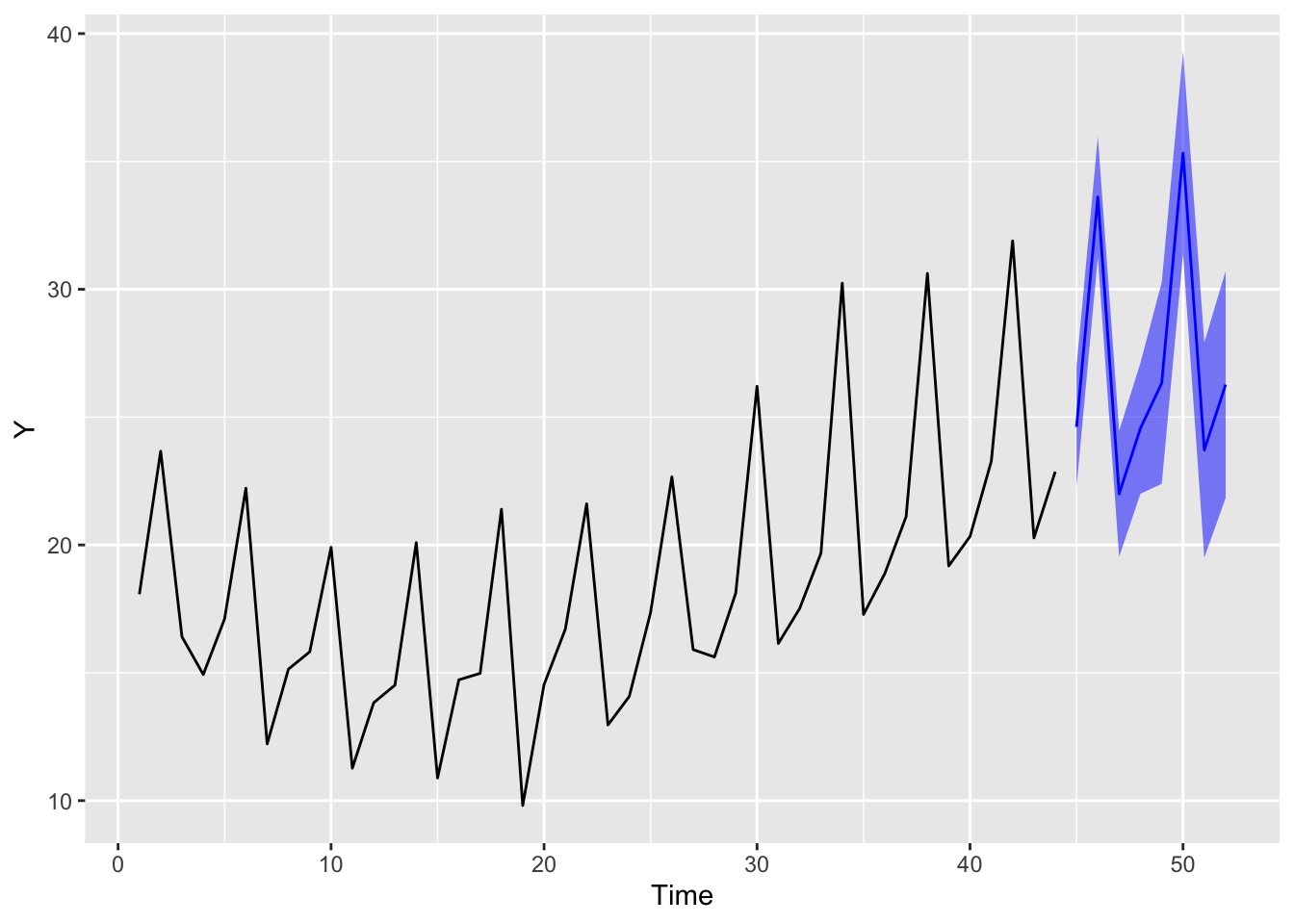
dlmFilter関数でフィルタリングして、dlmForecast関数で予測します。ここでは8期先まで予測しました。予測値の分散(pre$Q)を通常のベクトルに変換した後、平方根をとって標準偏差としています。予測値とその95%信頼区間をプロットしました。
fil <- dlmFilter(data$Y, mod)
pre <- dlmForecast(fil, nAhead = 8)
sd <- sqrt(unlist(pre$Q))
Fore <- data.frame(Time = max(data$Time) + 1:8,
Forecast = pre$f,
Lower = pre$f + qnorm(0.025) * sd,
Upper = pre$f + qnorm(0.975) * sd)
p +
geom_ribbon(data = Fore, aes(x = Time, ymin = Lower, ymax = Upper),
fill = "blue", alpha = 0.5) +
geom_line(data = Fore, aes(x = Time, y = Forecast), color = "blue")