library(DiagrammeR)
library(GGally)
## 要求されたパッケージ ggplot2 をロード中です
## Registered S3 method overwritten by 'GGally':
## method from
## +.gg ggplot2
library(lavaan)
## This is lavaan 0.6-16
## lavaan is FREE software! Please report any bugs.
set.seed(1234)林・黒木(2016)にある、交絡および中間変数によるバイアスをシミュレーションで確認してみました。
- 林岳彦・黒木学 (2016) 相関と因果と丸と矢印のはなし—はじめてのバックドア基準—. 岩波データサイエンスVol.3: 28–48.
交絡
データ
以下のようなデータを用意しました。
N <- 200
beta1 <- c(0.7, 2, 0.5)
z <- rnorm(N, 0, 1)
x <- beta1[1] * z + rnorm(N, 0, 1)
y <- beta1[2] * x + beta1[3] * z + rnorm(N, 0, 2)
df1 <- data.frame(z = z, x = x, y = y)\(z\)が、\(x\)→\(y\)の関係の交絡因子になっています。

散布図行列をみてみます。
ggpairs(df1)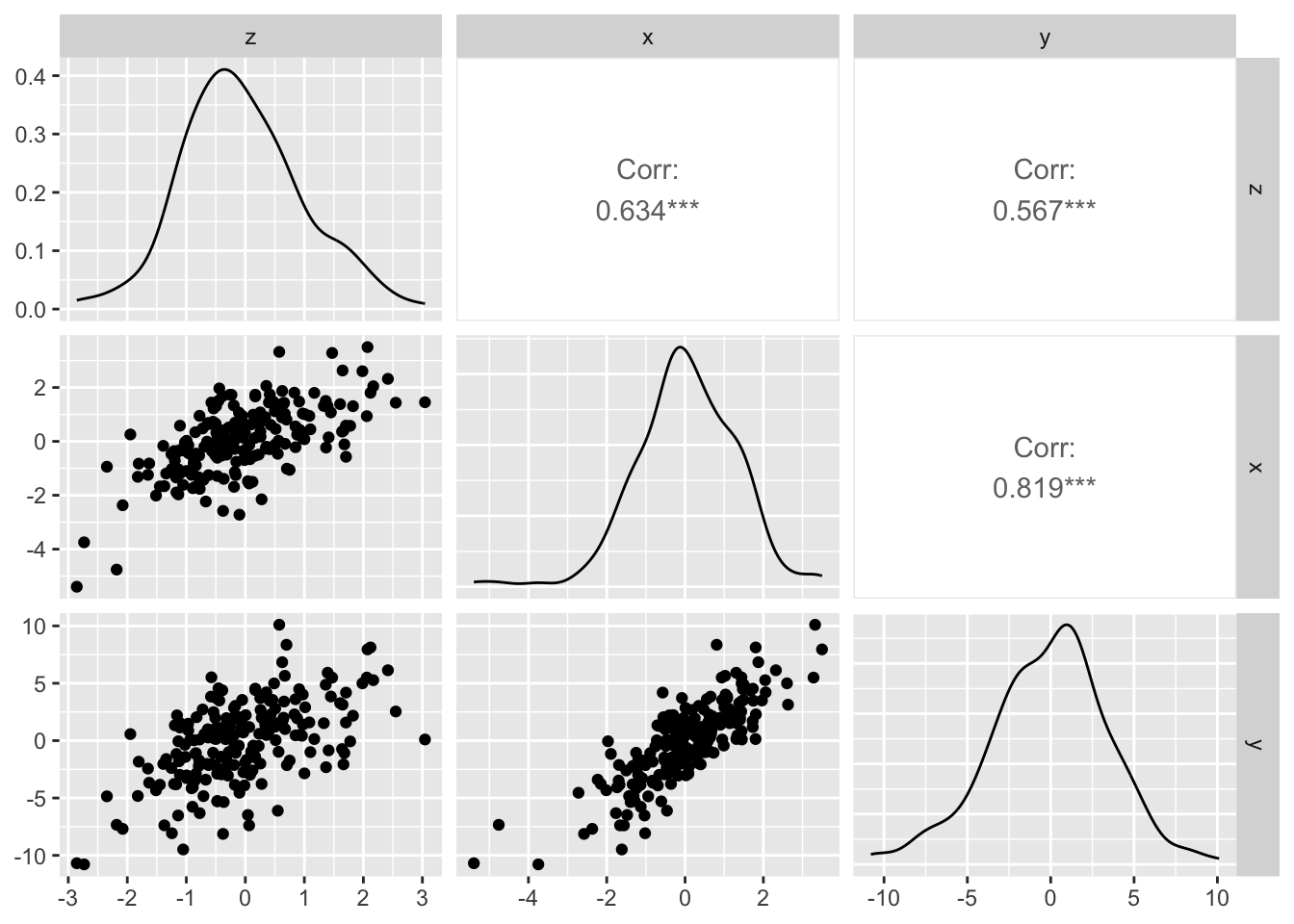
回帰
\(z\)を入れないで回帰してみます。
lm(y ~ x, data = df1) |>
summary()
##
## Call:
## lm(formula = y ~ x, data = df1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -5.6237 -1.4965 -0.0608 1.3693 6.7193
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.1964 0.1459 -1.346 0.18
## x 2.2695 0.1129 20.106 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.062 on 198 degrees of freedom
## Multiple R-squared: 0.6712, Adjusted R-squared: 0.6696
## F-statistic: 404.3 on 1 and 198 DF, p-value: < 2.2e-16真値の2からずれるようです。
シミュレーション
1回だけではよくわからないので、2000回繰り返してみます。
fun1 <- function(N = 100, beta) {
z <- rnorm(N, 0, 1)
x <- beta1[1] * z + rnorm(N, 0, 1)
y <- beta[2] * x + beta[3] * z + rnorm(N, 0, 2)
coef1x <- coef(lm(y ~ x))["x"]
coef2x <- coef(lm(y ~ x + z))["x"]
c(coef1x, coef2x)
}
coef1 <- replicate(2000, fun1(N = 200, beta = beta1))
summary(coef1[1, ])
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.758 2.146 2.226 2.231 2.313 2.674
summary(coef1[2, ])
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.434 1.903 1.997 1.999 2.094 2.511記事にあるように、\(z\)を説明変数に入れないと、\(x\)の係数が、\(\beta_{Z,Y} \frac{\mathrm{cov}(X,Z)}{\mathrm{var}(X)}\)だけずれます。
中間変数
データ
以下のようなデータを用意しました。
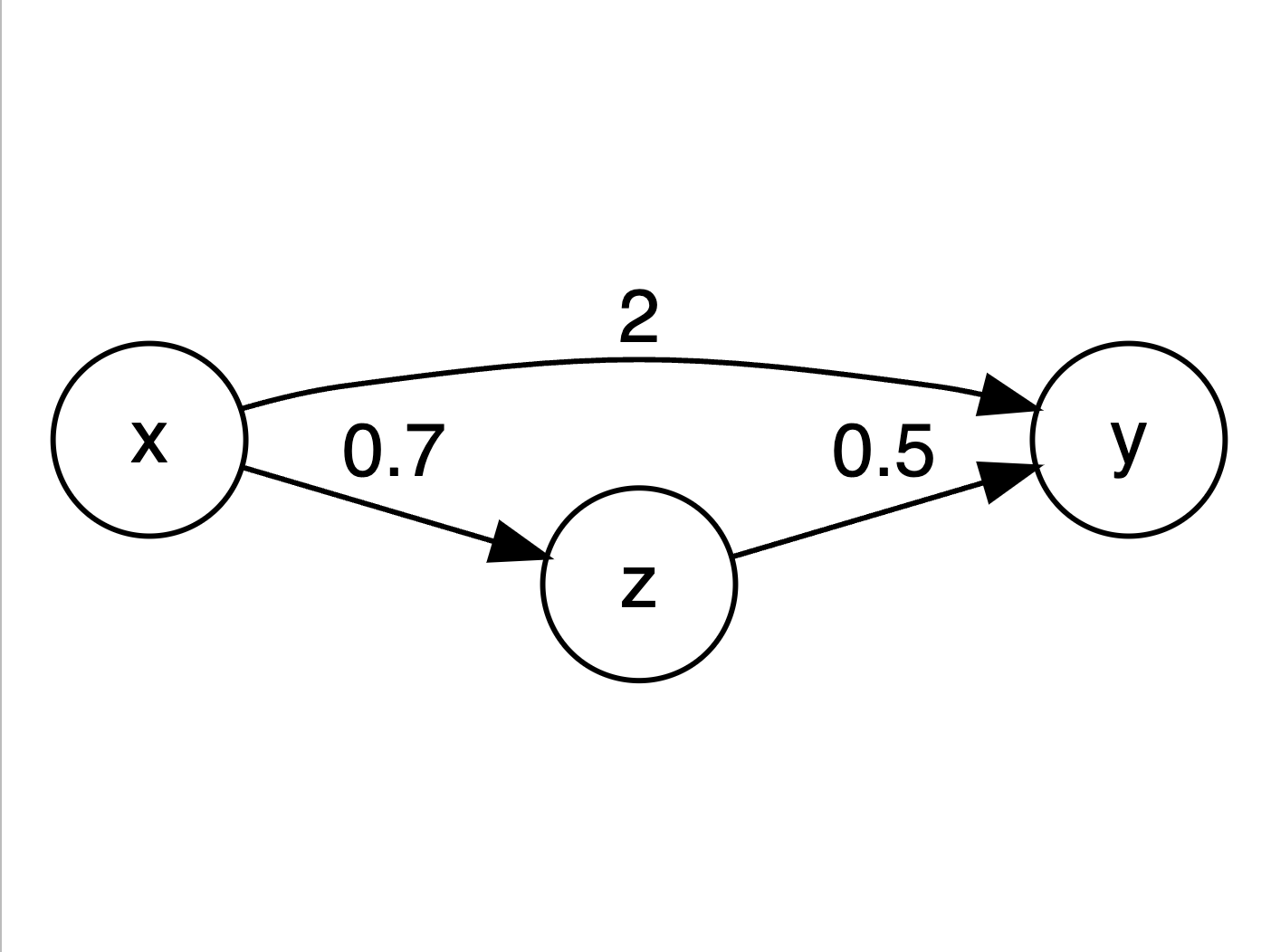
beta2 <- c(0.7, 2, 0.5)
x <- rnorm(N, 0, 1)
z <- beta2[1] * x + rnorm(N, 0, 1)
y <- beta2[2] * x + beta2[3] * z + rnorm(N, 0, 2)
df2 <- data.frame(z = z, x = x, y = y)\(z\)が、\(x\)→\(y\)の関係の中間変数になっています。
散布図行列をみてみます。
ggpairs(df2)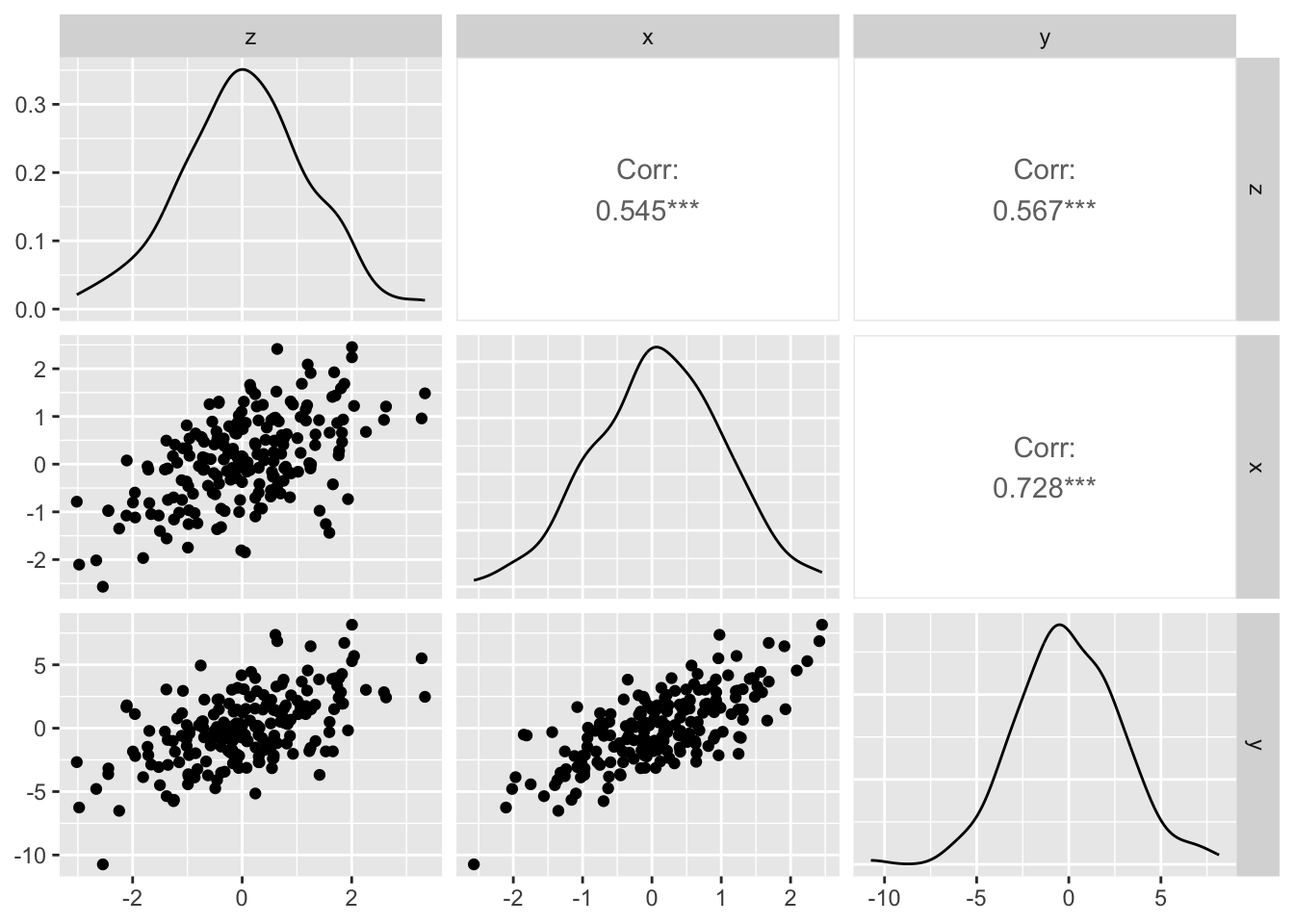
回帰
\(x\)が\(y\)におよぼす効果は、2+0.7×0.5=2.35となります。
中間変数の\(z\)を入れて回帰してみます。
lm(y ~ x + z, data = df2) |>
summary()
##
## Call:
## lm(formula = y ~ x + z, data = df2)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.6416 -1.3156 0.1145 1.0189 5.4368
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.2121 0.1332 -1.593 0.113
## x 1.8296 0.1705 10.733 < 2e-16 ***
## z 0.5875 0.1349 4.356 2.13e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.872 on 197 degrees of freedom
## Multiple R-squared: 0.5719, Adjusted R-squared: 0.5675
## F-statistic: 131.6 on 2 and 197 DF, p-value: < 2.2e-16当然ながら、偏回帰係数の2が求まります。
シミュレーション
中間変数\(z\)を説明変数に入れない場合と、入れた場合とを比較して見ます。2000回の繰り返しです。
fun2 <- function(N = 100, beta) {
x <- rnorm(N, 0, 1)
z <- beta[1] * x + rnorm(N, 0, 1)
y <- beta[2] * x + beta[3] * z + rnorm(N, 0, 2)
coef1x <- coef(lm(y ~ x))["x"]
coef2x <- coef(lm(y ~ x + z))["x"]
c(coef1x, coef2x)
}
coef2 <- replicate(2000, fun2(N = 200, beta = beta2))
summary(coef2[1, ])
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.838 2.252 2.348 2.349 2.446 2.977
summary(coef2[2, ])
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.398 1.885 2.000 2.000 2.110 2.597\(z\)を説明変数に入れると、その\(x\)の効果は偏回帰係数の分だけになります。
パス解析
せっかくなので、パス解析もやってみました。データは、1回だけの回帰でそれぞれ用いたものです。
交絡
model1 = "
x ~ beta_xz * z
y ~ beta_yx * x + beta_yz * z
# indirect effect
indirect_yz := beta_xz * beta_yx
# total effect
total_yz := beta_yz + indirect_yz
"
fit1 <- sem(model1, data = df1)
summary(fit1)
## lavaan 0.6.16 ended normally after 1 iteration
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 5
##
## Number of observations 200
##
## Model Test User Model:
##
## Test statistic 0.000
## Degrees of freedom 0
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## x ~
## z (bt_x) 0.805 0.069 11.599 0.000
## y ~
## x (bt_yx) 2.129 0.144 14.743 0.000
## z (bt_yz) 0.281 0.183 1.536 0.125
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .x 0.998 0.100 10.000 0.000
## .y 4.161 0.416 10.000 0.000
##
## Defined Parameters:
## Estimate Std.Err z-value P(>|z|)
## indirect_yz 1.713 0.188 9.116 0.000
## total_yz 1.994 0.205 9.745 0.000このデータでは、x→yの係数は2.129と推定されました(乱数のため真値からすこしずれます)。
なお、z→yの間接効果は1.713、総合効果は1.994と推定されました。
中間変数
model2 = "
z ~ beta_zx * x
y ~ beta_yx * x + beta_yz * z
# indirect effect
indirect_yx := beta_zx * beta_yz
# total effect
total_yx := beta_yx + indirect_yx
"
fit2 <- sem(model2, data = df2)
summary(fit2)
## lavaan 0.6.16 ended normally after 1 iteration
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 5
##
## Number of observations 200
##
## Model Test User Model:
##
## Test statistic 0.000
## Degrees of freedom 0
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## z ~
## x (bt_z) 0.688 0.075 9.184 0.000
## y ~
## x (bt_yx) 1.830 0.169 10.814 0.000
## z (bt_yz) 0.588 0.134 4.389 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .z 0.963 0.096 10.000 0.000
## .y 3.451 0.345 10.000 0.000
##
## Defined Parameters:
## Estimate Std.Err z-value P(>|z|)
## indirect_yx 0.404 0.102 3.960 0.000
## total_yx 2.234 0.149 15.037 0.000このデータでは、総合効果は2.234と推定されました。