線形回帰モデルの診断 – 伊東生態統計研究室

R標準のlm関数で線形回帰モデルを当てはめた結果のオブジェクトにplot関数を適用すると回帰診断のプロットが表示されます。外れ値のあるデータや、線形ではないデータをあてはめた場合どのように表示されるのか見てみました。

これについては、『統計学実践ワークブック』の第17章に詳しい説明があります。

線形正規分布のデータ

線形正規分布のデータを生成し、プロットします。

set.seed(1234)

N <- 100
x <- rnorm(N, 0, 2)
y1 <- x + rnorm(N, 0, 1)
plot(x, y1)

lm関数で線形回帰モデルをあてはめ、結果をプロットします。

lm1 <- lm(y1 ~ x)
plot(lm1)

最初のプロットは、残差プロットです。予測値と残差との関係をしめしています。残差が予測値に対して均等に分布していることが見てとれます。

2番目のプロットは、正規Q-Qプロットです。誤差項の正規性の仮定が満たされていれば、傾き1の直線にのります。このデータでは（そのようにつくっているので）問題なさそうです。

3番目のプロットは、標準化残差の絶対値の平方根プロットです。点に増加傾向や減少傾向があると、等分散性が成り立っていないことが疑われます。このデータでは問題なさそうです（そのようにつくっています）。

最後のプロットは、てこ比と標準化残差との関係とCookの距離を示したものです。てこ比の大きなデータはモデルへの影響が大きいことをしめします。Cookの距離が0.5を超えていると、外れ値とされるということです。このデータでは外れ値はなさそうです。

先ほどのデータの最初の5個を置き換えて、外れ値としました。外れ値を赤色でプロットします。

y2 <- c(rnorm(5, 10, 1), y1[-(1:5)])
plot(x[-(1:5)], y2[-(1:5)], ylim = c(min(y2), max(y2)))
points(x[1:5], y2[1:5], col = "red")

lm2 <- lm(y2 ~ x)
plot(lm2)

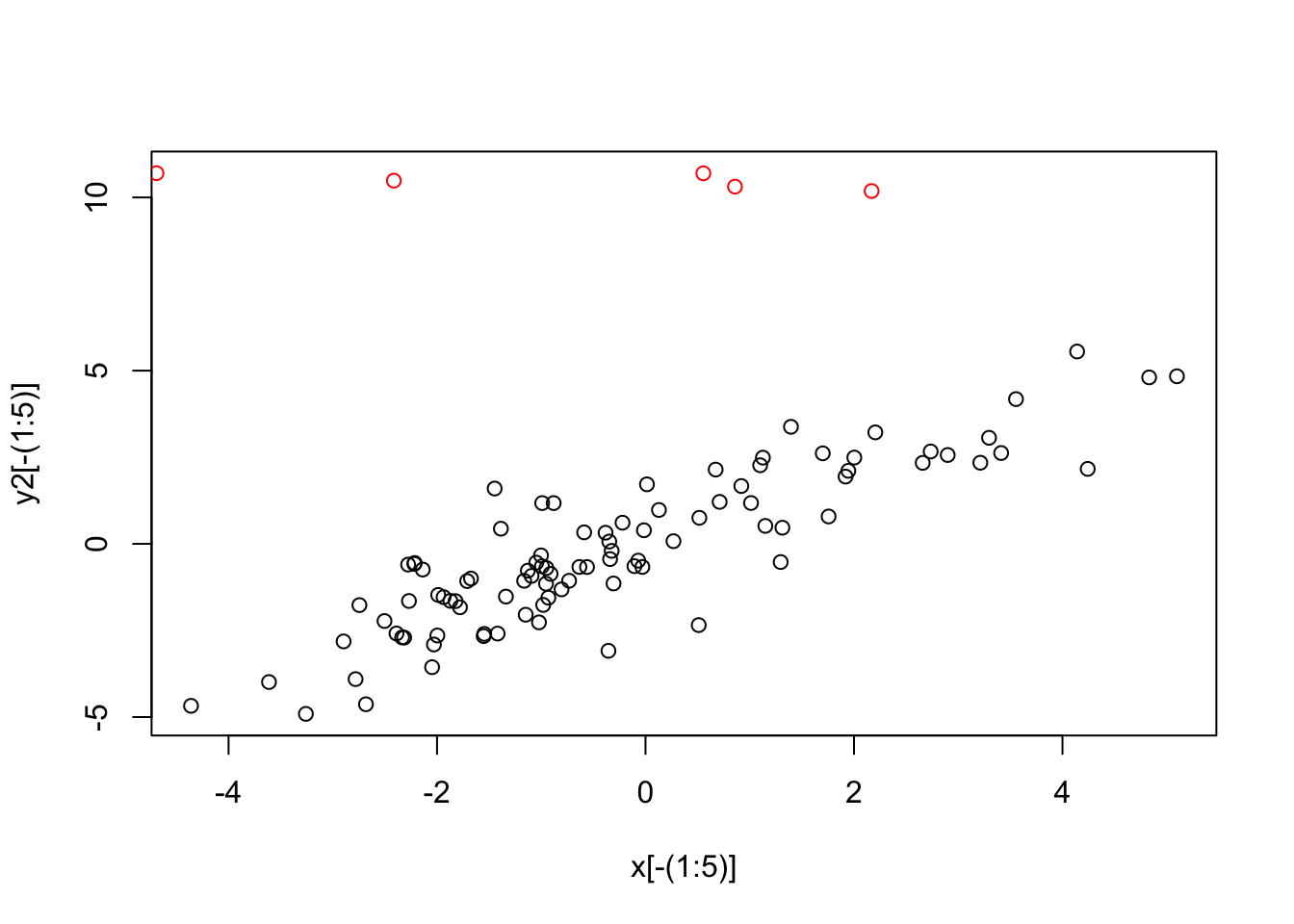
1番目から3番目のプロットでは外れ値が見てとれます。4番目のプロットのCookの距離は、点4だけが0.5を超えていますが、外れ値として設定したその他の点も、その他の点のかたまりから外れています。

ポアソン分布のデータを生成します。

y3 <- rpois(N, exp(x))
plot(x, y3)

このデータをむりやり線形回帰モデルにあてはめてみます。

lm3 <- lm(y3 ~ x)
plot(lm3)

1番目の3番目のプロットでは等分散性が成り立っていないことが示されています。2番目の正規Q-Qプロットも両端が大きく外れています。4番目のプロットのCookの距離も、点20と60で0.5を超えていますし、点のかたまりにもなんだか構造がみえています。

実際のデータでは微妙な場合も多いかもしれませんが、明らかに問題のある場合はこれで見てわかると思われます。