bayesplotパッケージによる事後予測検査

R
Stan
作者

伊東宏樹

公開

2023年9月23日

更新日

2023年9月25日

事後予測検査 (Posterior predictive check) は、モデルの評価のため、目的変数の事後予測分布から複製データを抽出して、それと観測値とがどのくらい整合がとれているのかを確認するというものです。モデルがデータにあっていなければ、複製データと観測値との間に大きな差が生じることになります。

Stanの開発チームが作成しているbayesplotパッケージでは、事後予測検査のための関数が多数ふくまれています。

準備

cmdstanr経由でStanを使用します。

library(cmdstanr)
## This is cmdstanr version 0.6.1
## - CmdStanR documentation and vignettes: mc-stan.org/cmdstanr
## - CmdStan path: /usr/local/cmdstan
## - CmdStan version: 2.33.1
register_knitr_engine()
library(posterior)
## This is posterior version 1.4.1
## 
##  次のパッケージを付け加えます: 'posterior'
##  以下のオブジェクトは 'package:stats' からマスクされています:
## 
##     mad, sd, var
##  以下のオブジェクトは 'package:base' からマスクされています:
## 
##     %in%, match
library(bayesplot)
## This is bayesplot version 1.10.0
## - Online documentation and vignettes at mc-stan.org/bayesplot
## - bayesplot theme set to bayesplot::theme_default()
##    * Does _not_ affect other ggplot2 plots
##    * See ?bayesplot_theme_set for details on theme setting
## 
##  次のパッケージを付け加えます: 'bayesplot'
##  以下のオブジェクトは 'package:posterior' からマスクされています:
## 
##     rhat
library(ggplot2)
set.seed(123)

データ

目的変数Yが対数正規分布するデータを生成します。

N <- 100
X <- runif(N, 0, 6)
mu <- -1 + 0.25 * X
Y <- rlnorm(N, meanlog = mu, sdlog = 1)
stan_data <- list(N = N, X = X, Y = Y)

生成されたデータを確認します。

data.frame(X = X, Y = Y) |>
  ggplot() +
  geom_point(aes(x = X, y = Y))

モデル1

まずは、通常の線形回帰モデルをあてはめてみます。

generated quantitiesブロックで、複製データyrepを生成するようにしています。

data {
  int<lower=0> N;
  vector[N] X;
  vector[N] Y;
}

parameters {
  array[2] real beta;
  real<lower=0> sigma;
}

transformed parameters {
  vector[N] mu = beta[1] + beta[2] * X;
}

model {
  Y ~ normal(mu, sigma);
}

generated quantities {
  vector[N] yrep;

  for (n in 1:N)
    yrep[n] = normal_rng(mu[n], sigma);
}

あてはめ

fit1 <- model1$sample(data = stan_data,
                      iter_warmup = 1000, iter_sampling = 1000,
                      refresh = 0)
## Running MCMC with 4 sequential chains...
## 
## Chain 1 finished in 0.1 seconds.
## Chain 2 finished in 0.1 seconds.
## Chain 3 finished in 0.1 seconds.
## Chain 4 finished in 0.1 seconds.
## 
## All 4 chains finished successfully.
## Mean chain execution time: 0.1 seconds.
## Total execution time: 0.5 seconds.
fit1$summary(c("beta", "sigma"))
## # A tibble: 3 × 10
##   variable  mean median    sd    mad     q5   q95  rhat ess_bulk ess_tail
##   <chr>    <num>  <num> <num>  <num>  <num> <num> <num>    <num>    <num>
## 1 beta[1]  0.301  0.309 0.346 0.341  -0.267 0.870  1.00    1436.    1916.
## 2 beta[2]  0.330  0.331 0.101 0.0952  0.162 0.499  1.00    1493.    1820.
## 3 sigma    1.71   1.71  0.122 0.121   1.52  1.93   1.00    1985.    1952.

事後予測検査

Stanモデル中の複製データyrepのMCMCサンプルを取り出して、yrep1に入れておきます。

yrep1 <- fit1$draws("yrep", format = "draws_matrix")

bayesplotパッケージにある事後予測検査の関数をいくつか適用していきます。

ppc_dens_overlay

複製データyrep1と元データYとの分布を比較します。yrep1は今回、4000繰り返し分あるので、その中から100個を取り出してプロットします。

ppc_dens_overlay(Y, yrep1[sample(dim(yrep1)[1], 100), ])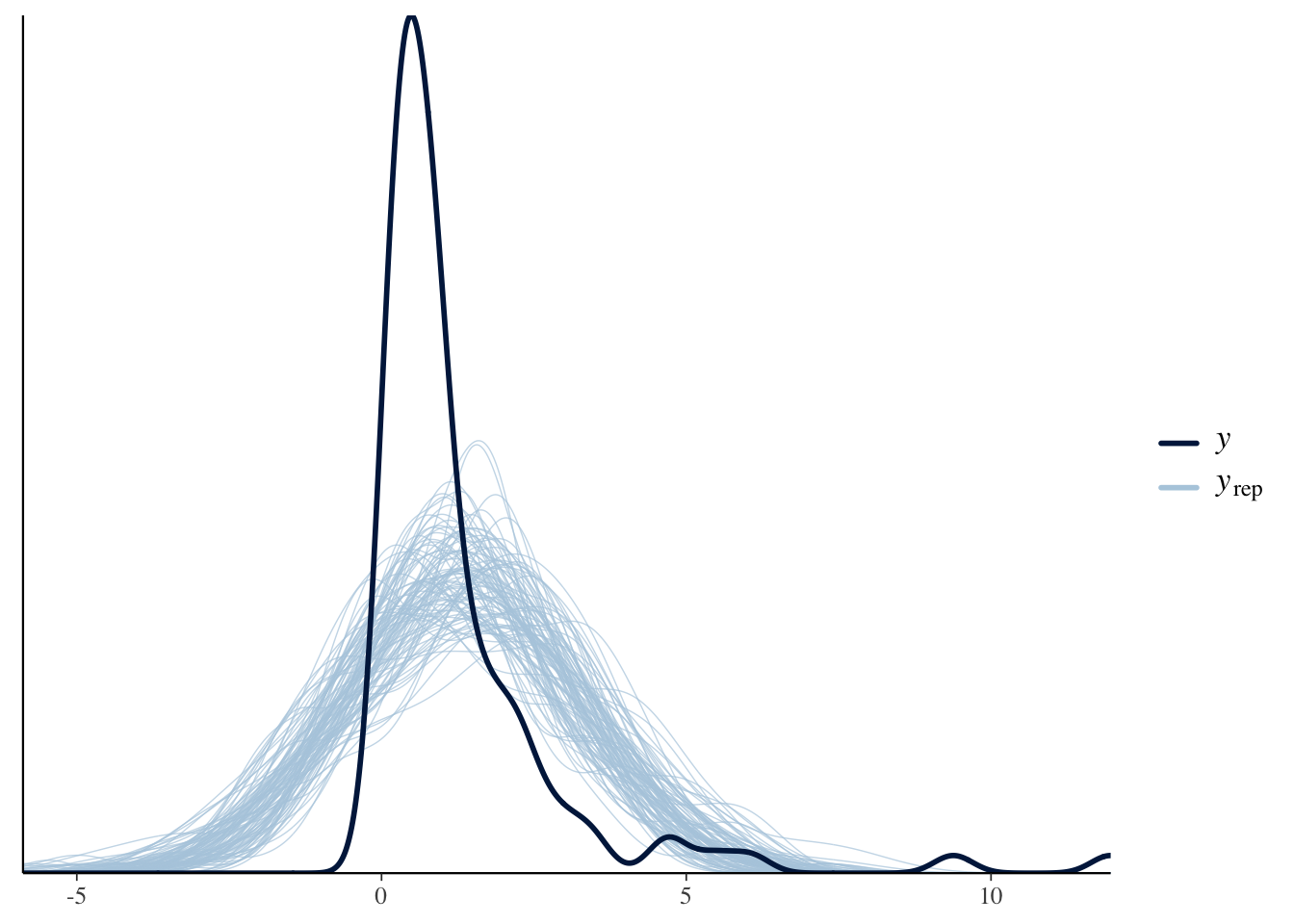

データとはズレが見られます。

ppc_intervals

各データ点について、事後予測分布の中央値と、50%および90%区間に、元データを重ねてプロットします。

ppc_intervals(Y, yrep1)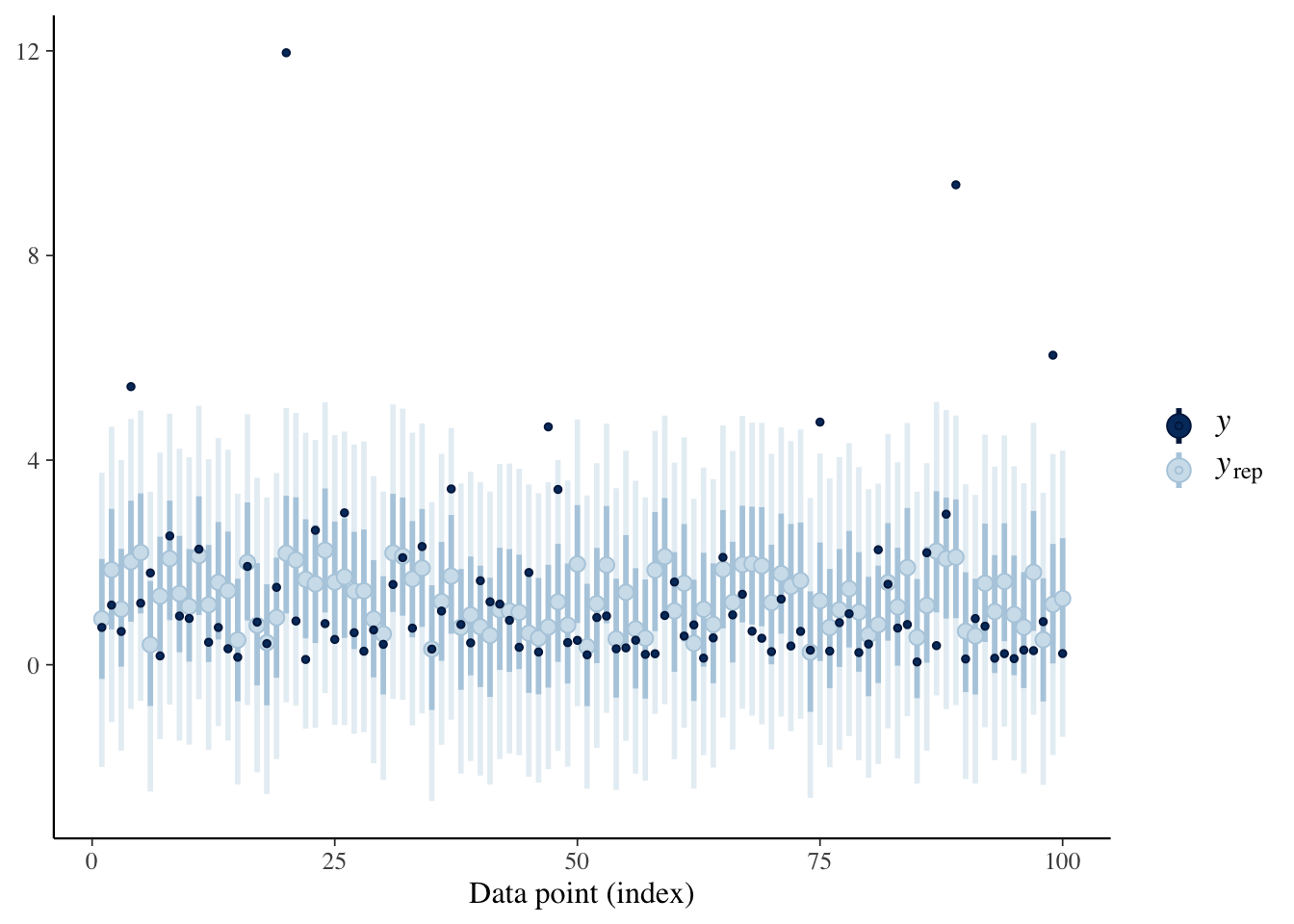

正規分布に当てはめているので、複製データの方では負の値が出たりしています。

ppc_ribbon

ppc_intervalsとほぼ同様ですが、リボン形式でプロットします。

ppc_ribbon(Y, yrep1)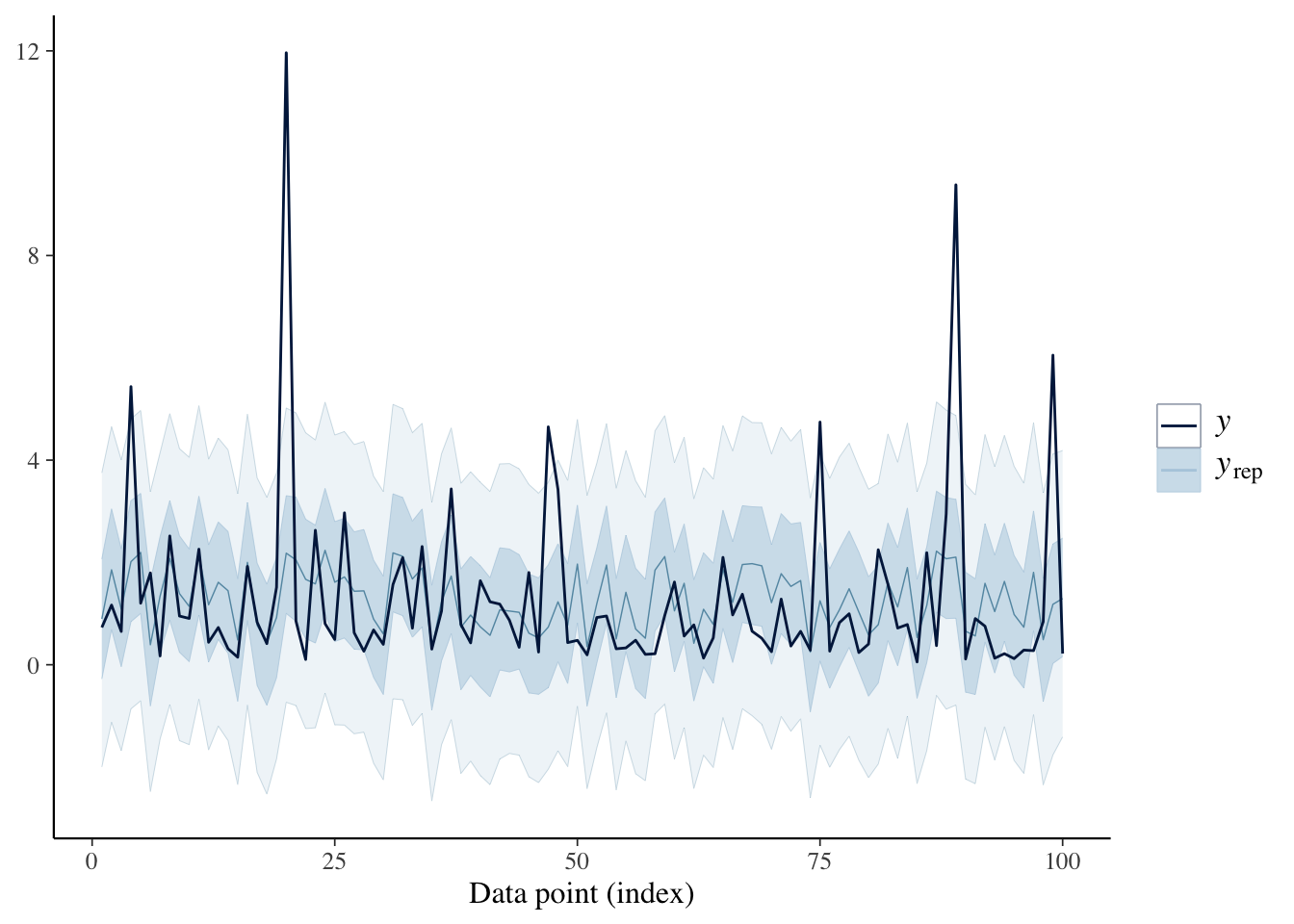

ppc_stat_2d

各繰り返しの平均と標準偏差に、元データの平均と標準偏差を重ねてプロットします。

ppc_stat_2d(Y, yrep1, stat = c("mean", "sd"))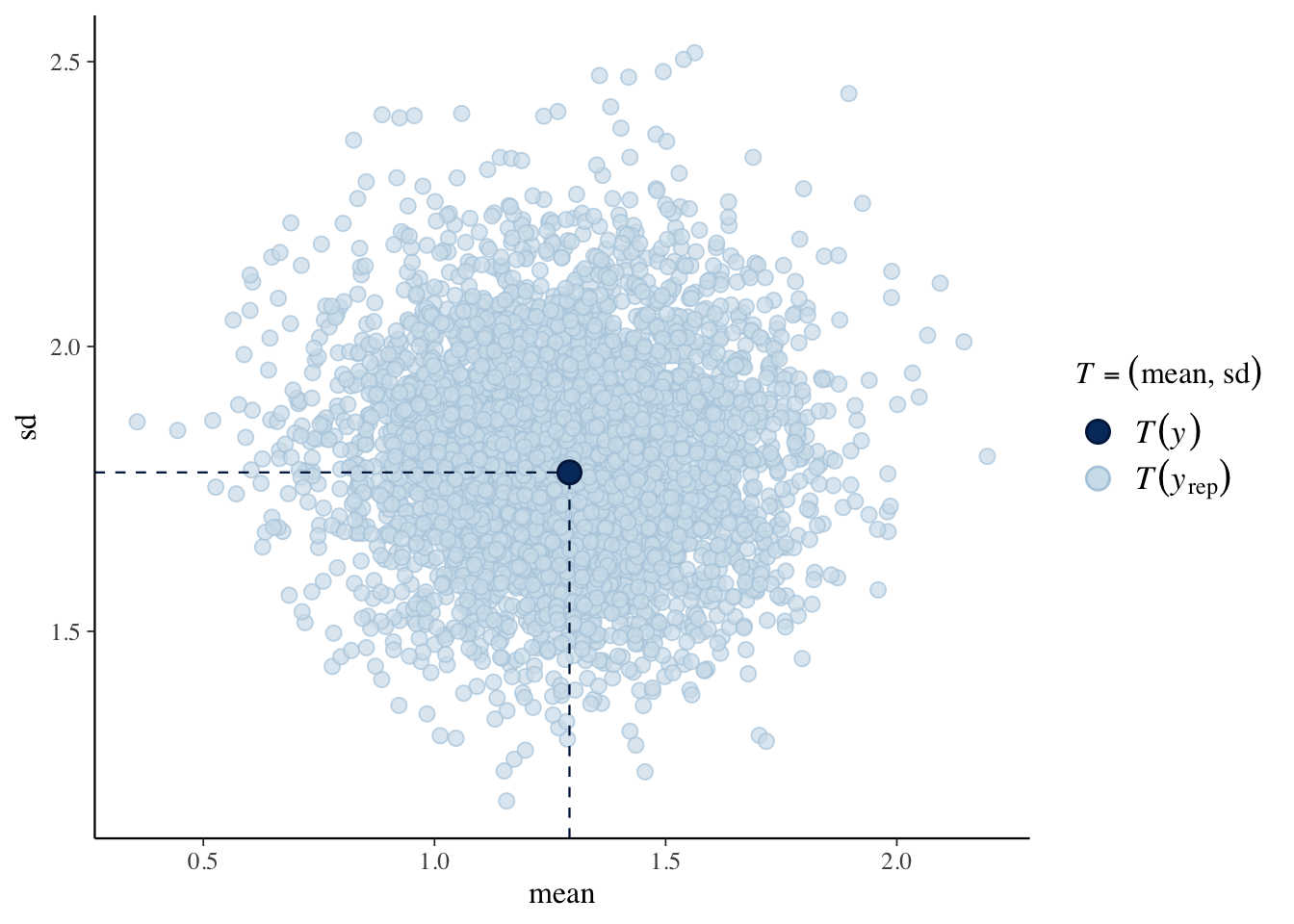

平均と標準偏差に関しては、うまく推定できているようです。

モデル2

つづいて、目的変数が対数正規分布にしたがうというモデルをあてはめます。すなわち、データを生成したモデルと同じです。

data {
  int<lower=0> N;
  vector[N] X;
  vector<lower=0>[N] Y;
}

parameters {
  array[2] real beta;
  real<lower=0> sigma;
}

transformed parameters {
  vector[N] mu = beta[1] + beta[2] * X;
}

model {
  Y ~ lognormal(mu, sigma);
}

generated quantities {
  vector[N] yrep;
  real disc_obs = 0;
  real disc_rep = 0;

  for (n in 1:N)
    yrep[n] = lognormal_rng(mu[n], sigma);
}

あてはめ

fit2 <- model2$sample(data = stan_data,
                      iter_warmup = 1000, iter_sampling = 1000,
                      refresh = 0)
## Running MCMC with 4 sequential chains...
## 
## Chain 1 finished in 0.1 seconds.
## Chain 2 finished in 0.1 seconds.
## Chain 3 finished in 0.1 seconds.
## Chain 4 finished in 0.1 seconds.
## 
## All 4 chains finished successfully.
## Mean chain execution time: 0.1 seconds.
## Total execution time: 0.9 seconds.
fit2$summary(c("beta", "sigma"))
## # A tibble: 3 × 10
##   variable   mean median     sd    mad     q5    q95  rhat ess_bulk ess_tail
##   <chr>     <num>  <num>  <num>  <num>  <num>  <num> <num>    <num>    <num>
## 1 beta[1]  -1.01  -1.01  0.200  0.199  -1.35  -0.683  1.01    1520.    1564.
## 2 beta[2]   0.235  0.235 0.0585 0.0575  0.141  0.333  1.01    1591.    1794.
## 3 sigma     0.980  0.977 0.0713 0.0688  0.867  1.10   1.00    2264.    1868.

事後予測検査

モデル1のときと同様に、Stanモデルの複製データyrepのMCMCサンプルを取り出して、yrep2に入れておきます。

yrep2 <- fit2$draws("yrep", format = "draws_matrix")

以下は、モデル1のときと同様です。

ppc_dens_overlay

ppc_dens_overlay(Y, yrep2[sample(dim(yrep2)[1], 100), ])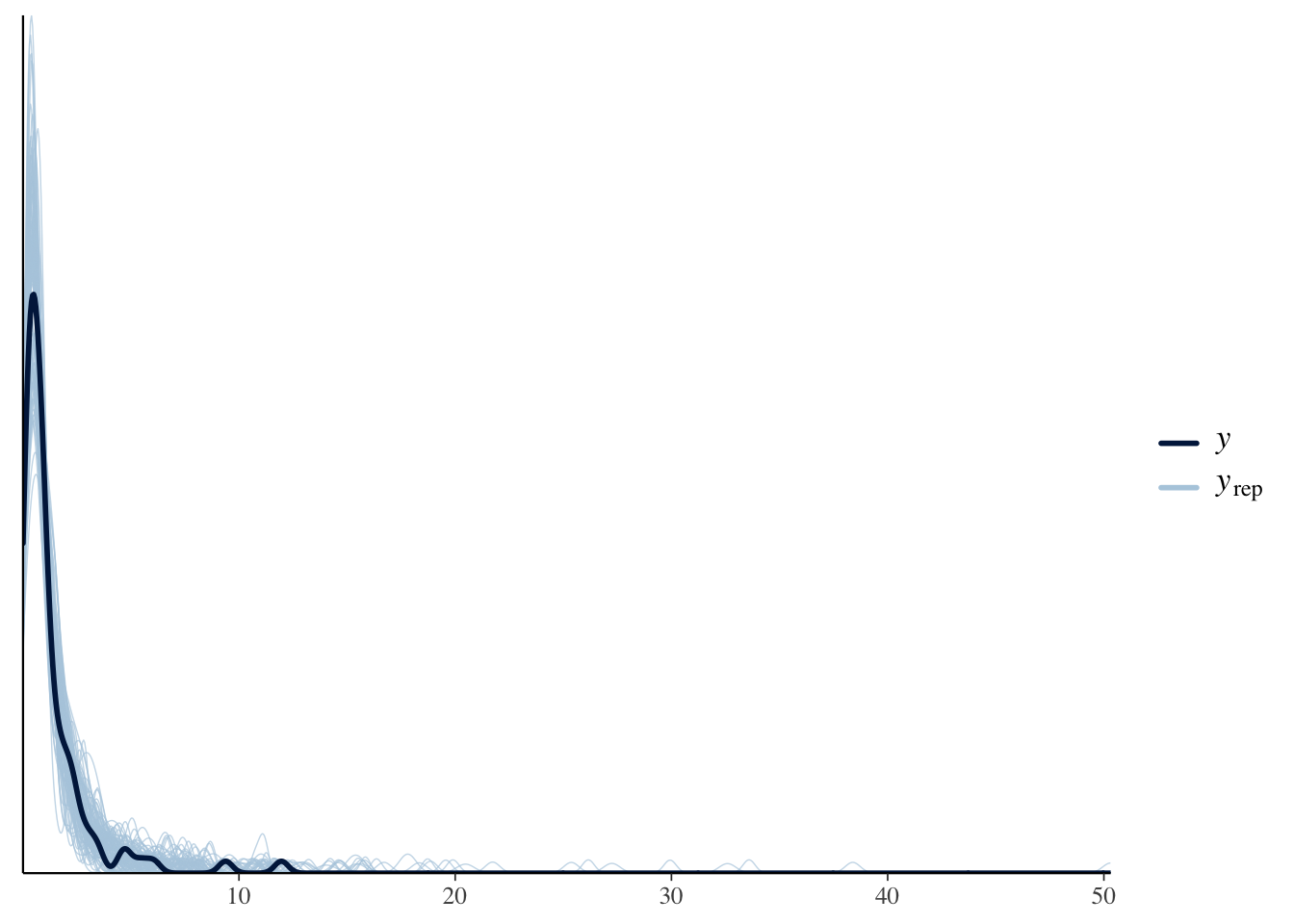

だいたい元データにあった分布になっています。

ppc_intervals

ppc_intervals(Y, yrep2)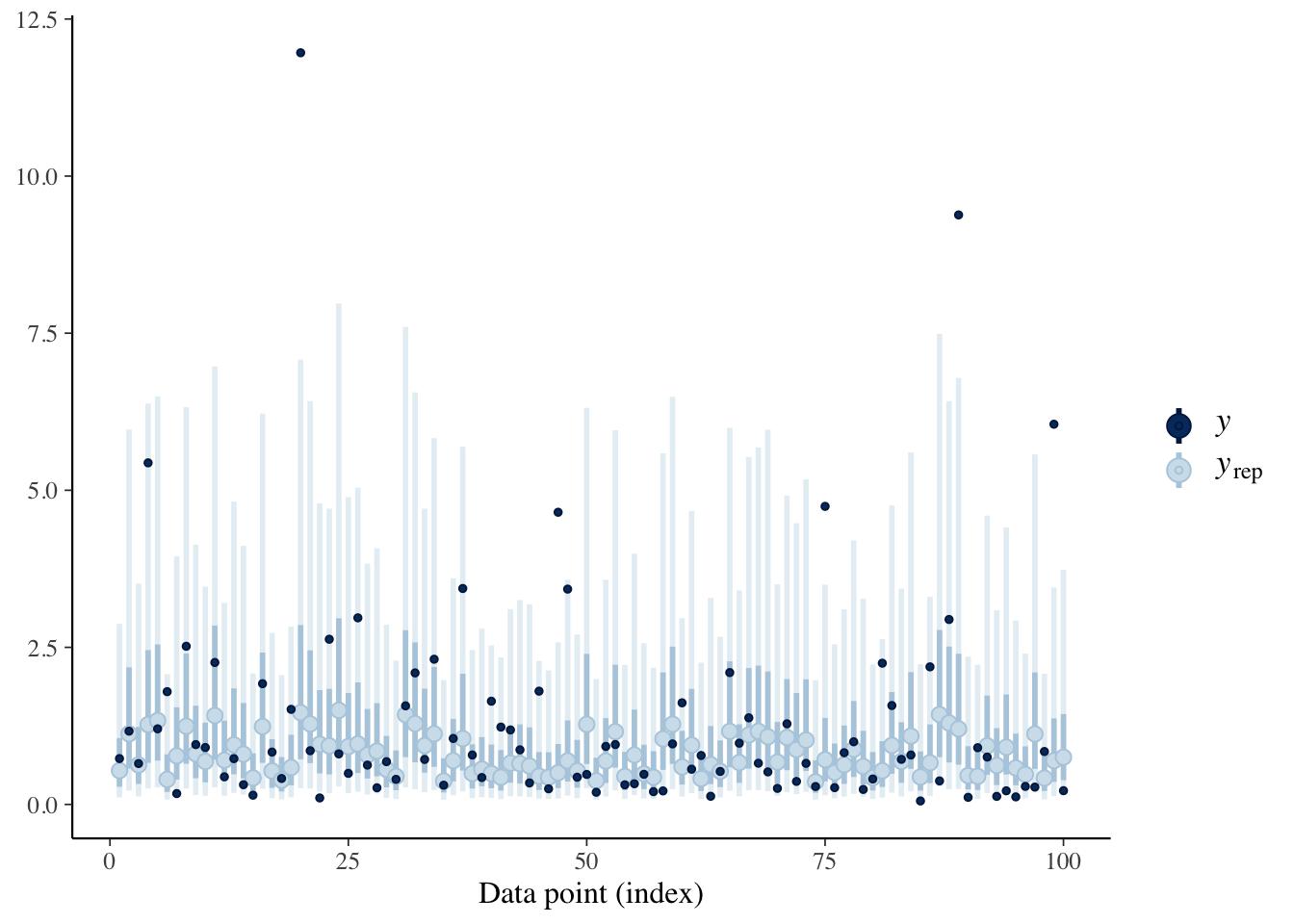

こちらも同様です。

ppc_ribbon

ppc_ribbon(Y, yrep2)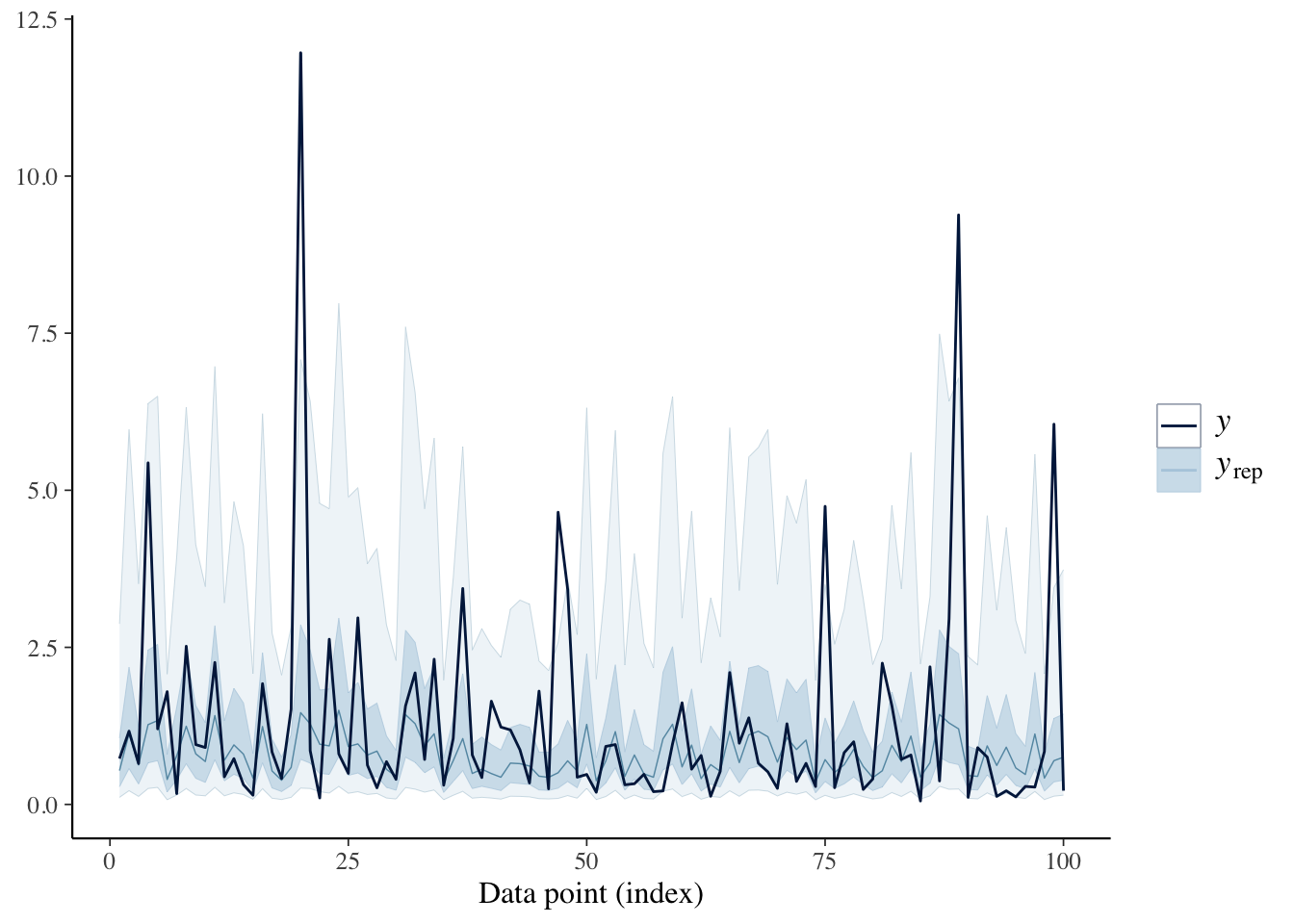

同様です。

ppc_stat_2d

ppc_stat_2d(Y, yrep2, stat = c("mean", "sd"))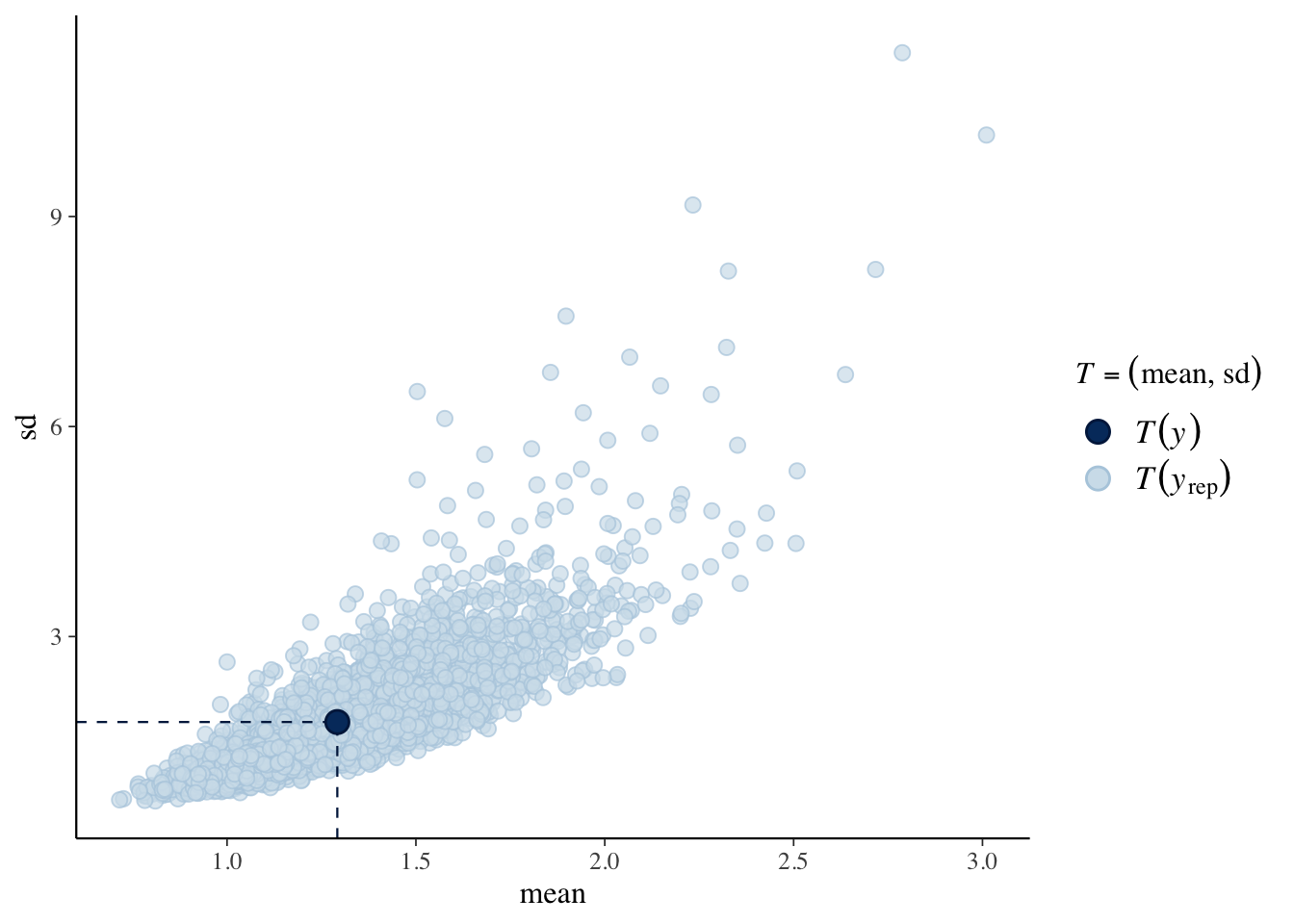

対数正規分布なので、複製データで大きな値が出たりしていますが、だいたいあっているようです。

おわりに

モデルが観測値にあっているとはなかなか言えませんが、事後予測検査で観測値と大きく違うような結果が出たならば、モデルが観測値にあっていないとは言えます。

bayesplotには事後予測検査の関数がまだほかにもありますので、興味のある方はGraphical posterior predictive checkingなどをご覧ください。