library(nimble)
## nimble version 1.0.1 is loaded.
## For more information on NIMBLE and a User Manual,
## please visit https://R-nimble.org.
##
## Note for advanced users who have written their own MCMC samplers:
## As of version 0.13.0, NIMBLE's protocol for handling posterior
## predictive nodes has changed in a way that could affect user-defined
## samplers in some situations. Please see Section 15.5.1 of the User Manual.
##
## 次のパッケージを付け加えます: 'nimble'
## 以下のオブジェクトは 'package:stats' からマスクされています:
##
## simulate
library(posterior)
## This is posterior version 1.4.1
##
## 次のパッケージを付け加えます: 'posterior'
## 以下のオブジェクトは 'package:stats' からマスクされています:
##
## mad, sd, var
## 以下のオブジェクトは 'package:base' からマスクされています:
##
## %in%, match
library(bayesplot)
## This is bayesplot version 1.10.0
## - Online documentation and vignettes at mc-stan.org/bayesplot
## - bayesplot theme set to bayesplot::theme_default()
## * Does _not_ affect other ggplot2 plots
## * See ?bayesplot_theme_set for details on theme setting
##
## 次のパッケージを付け加えます: 'bayesplot'
## 以下のオブジェクトは 'package:posterior' からマスクされています:
##
## rhat
library(dplyr)
##
## 次のパッケージを付け加えます: 'dplyr'
## 以下のオブジェクトは 'package:stats' からマスクされています:
##
## filter, lag
## 以下のオブジェクトは 'package:base' からマスクされています:
##
## intersect, setdiff, setequal, union
library(ggplot2)
set.seed(123)前回のつづきで、今回は離散値の場合をあつかいます。
準備
今回はNIMBLEを使用します。
データ
ゼロ過剰ポアソン分布のデータを用意します。
N <- 100
p <- 0.7
lambda <- 2.5
z <- rbinom(N, 1, p)
Y <- rpois(N, z * lambda)生成されたデータを確認します。
data.frame(Y = Y) |>
ggplot() +
geom_bar(aes(x = Y)) +
scale_x_continuous(breaks = 0:max(Y), minor_breaks = NULL)
モデル1
まずは、ポアソン分布をあてはめてみます。
複製データyrepの生成は、観測値Yのポアソン分布へのあてはめと同じコードになります。
code1 <- nimbleCode({
for (n in 1:N) {
Y[n] ~ dpois(lambda)
# replicated data
yrep[n] ~ dpois(lambda)
}
# prior
lambda ~ dunif(0, 100)
})あてはめ
初期化の関数init_funを定義して、nimbleMCMCでモデルをあてはめ、MCMCサンプルを取得します。後の利用のためにMCMCサンプルをcodaパッケージのmcmc.list型で出力するようにしています。
init_fun1 <- function() {
list(lambda = runif(1, 0, 2),
yrep = rpois(N, 1))
}
fit1 <- nimbleMCMC(code = code1,
constants = list(N = N),
data = list(Y = Y),
inits = init_fun1,
monitors = c("lambda", "yrep"),
nchains = 3,
niter = 2000, nburnin = 1000,
samplesAsCodaMCMC = TRUE)
## Defining model
## Building model
## Setting data and initial values
## Running calculate on model
## [Note] Any error reports that follow may simply reflect missing values in model variables.
## Checking model sizes and dimensions
## Checking model calculations
## Compiling
## [Note] This may take a minute.
## [Note] Use 'showCompilerOutput = TRUE' to see C++ compilation details.
## running chain 1...
## |-------------|-------------|-------------|-------------|
## |-------------------------------------------------------|
## running chain 2...
## |-------------|-------------|-------------|-------------|
## |-------------------------------------------------------|
## running chain 3...
## |-------------|-------------|-------------|-------------|
## |-------------------------------------------------------|パラメータlambdaについて結果の要約をみます。
fit1 |>
as_draws() |>
summarise_draws() |>
filter(variable == "lambda")
## # A tibble: 1 × 10
## variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
## <chr> <num> <num> <num> <num> <num> <num> <num> <num> <num>
## 1 lambda 1.74 1.74 0.140 0.137 1.51 1.96 1.00 666. 587.事後予測検査
複製データyrepのMCMCサンプルを取り出して、yrep1に入れておきます。
yrep1 <- fit1 |>
as_draws_df() |>
select(starts_with("yrep")) |>
as_draws_matrix()ppc_bars
複製データyrep1と観測値Yの分布を比較します。複製データの点は中央値、バーはデフォルトでは90%区間です。
ppc_bars(Y, yrep1)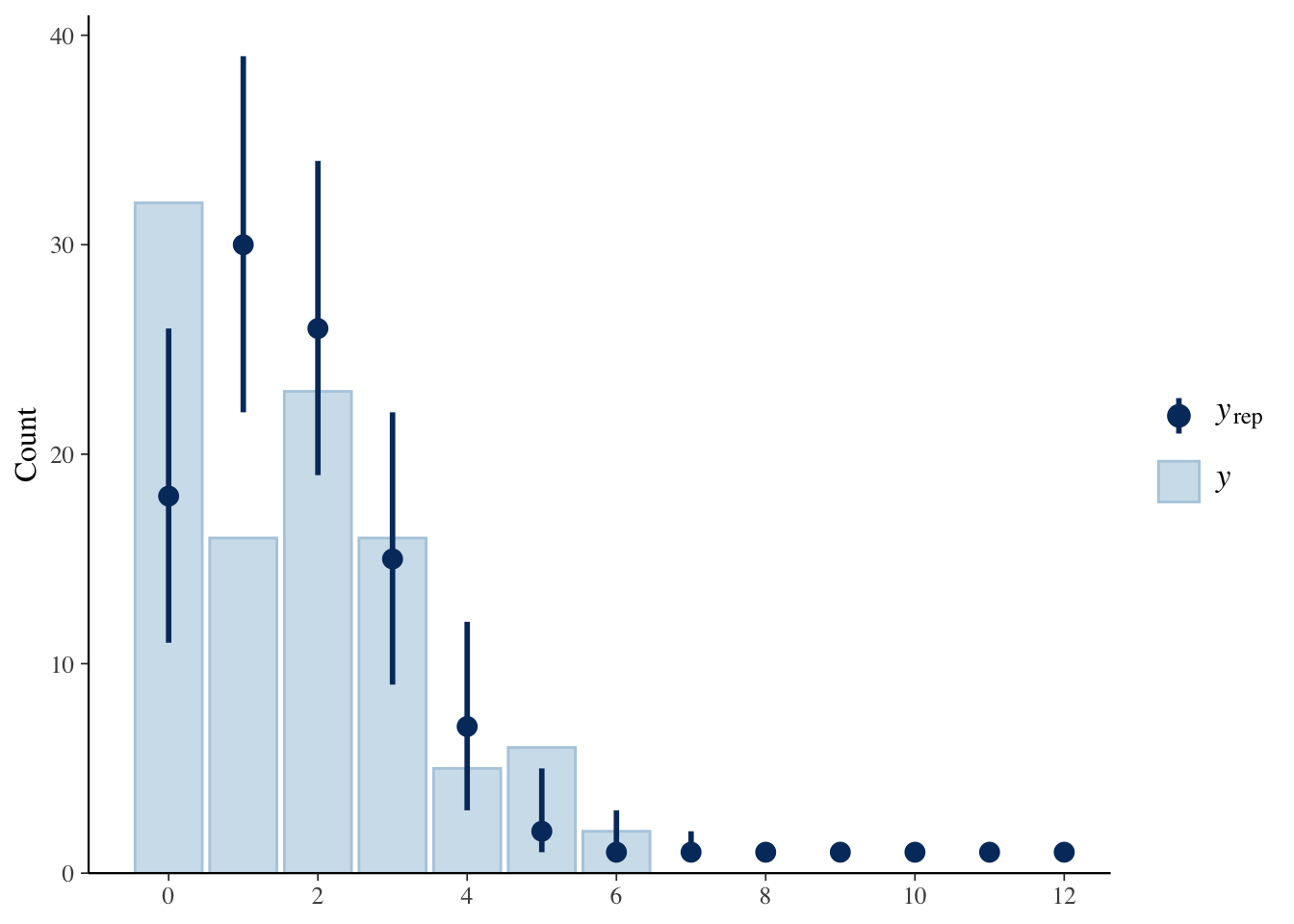
複製データは、とくに値が0と1のあたりで観測値とのあいだにズレがみられます。
ppc_rootogram
Rootgramでの比較です。表示方法には、“standing”, “hanging”, “suspended”の3種類があります。既定値の”standing”では、観測値のヒストグラムがそのまま表示され、“hanging”では、複製データの期待値からぶらさがって表示され、“suspended”では、期待値との差が表示されます。
ppc_rootogram(Y, yrep1, style = "standing")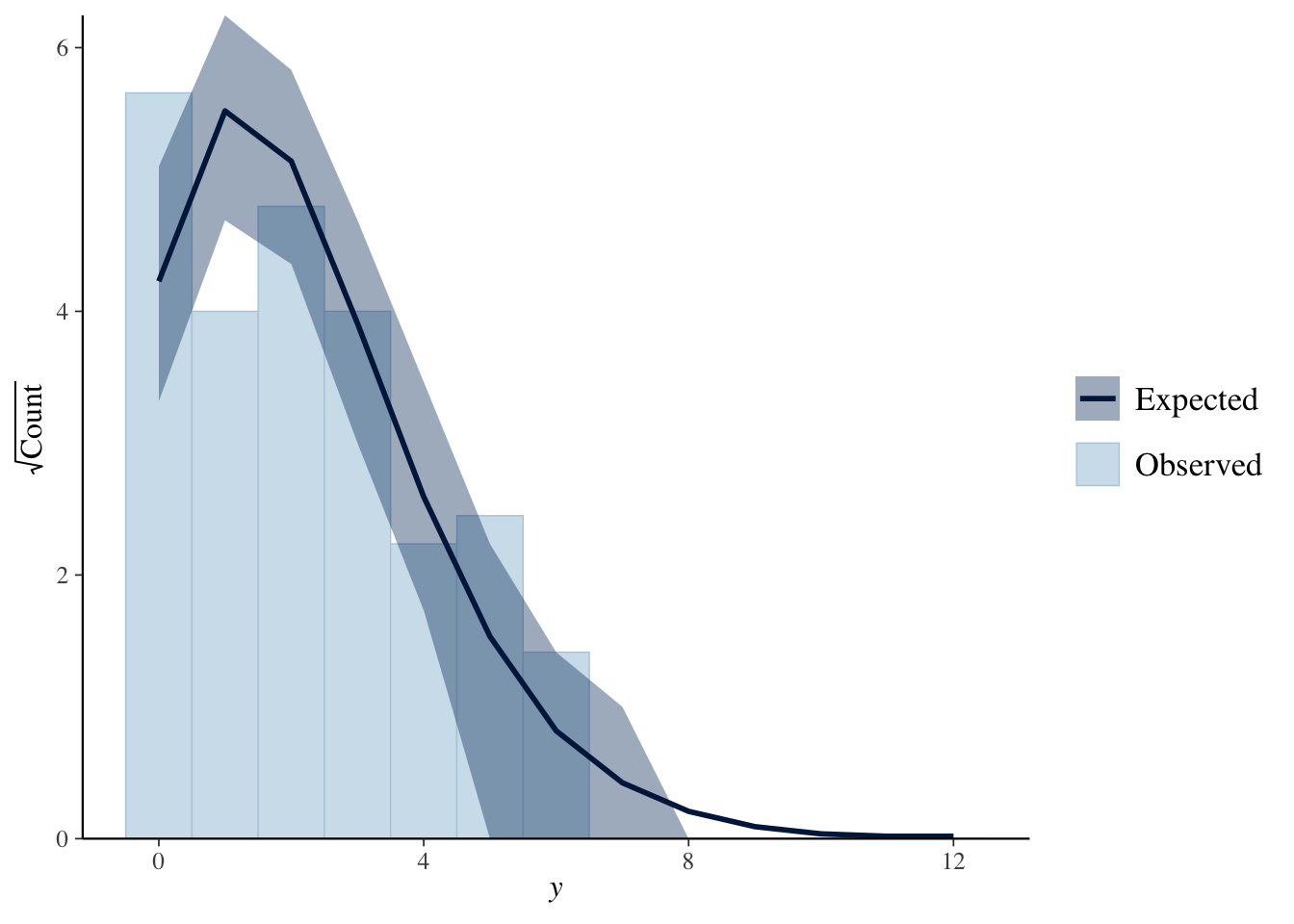
ppc_rootogram(Y, yrep1, style = "hanging")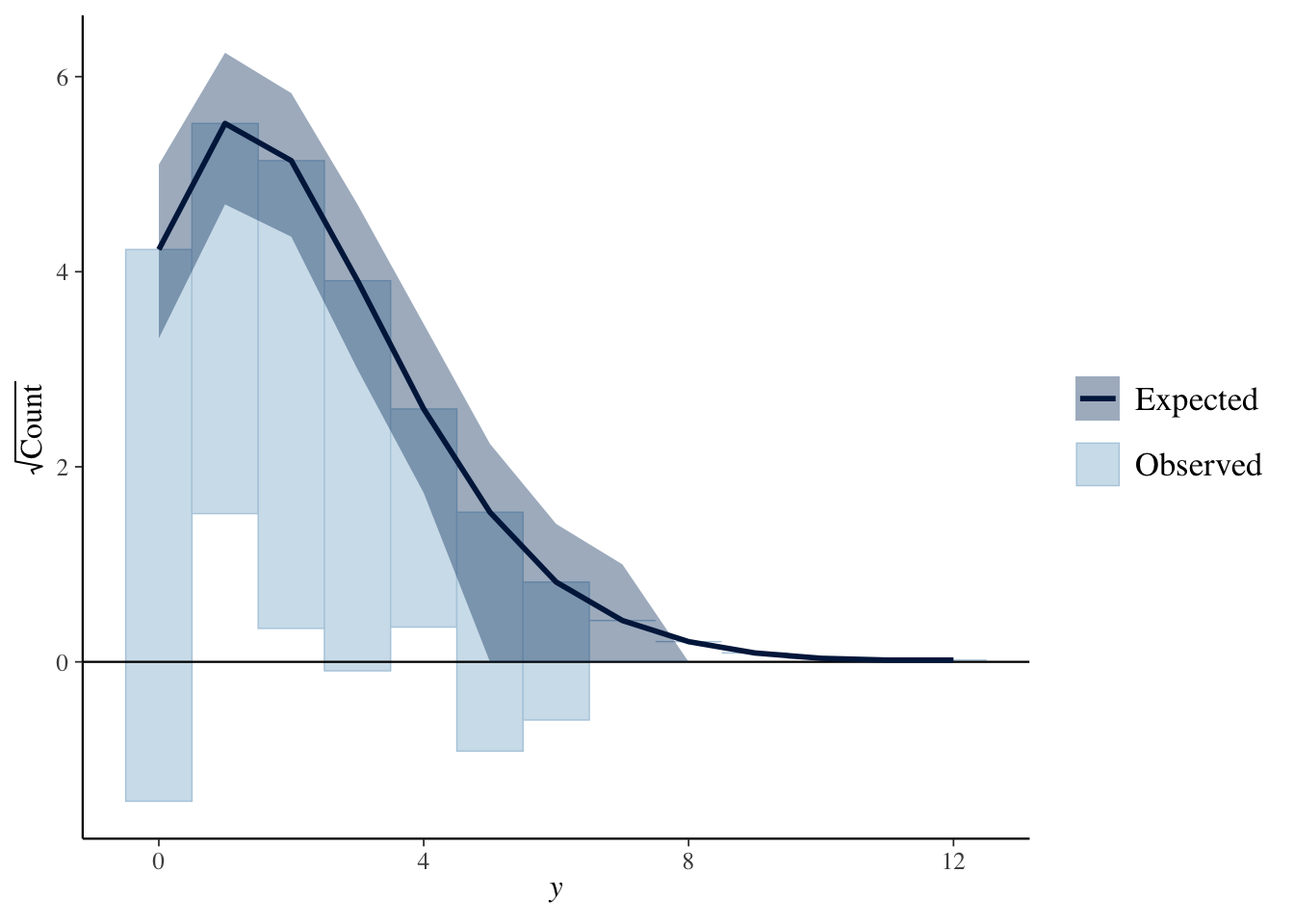
ppc_rootogram(Y, yrep1, style = "suspended")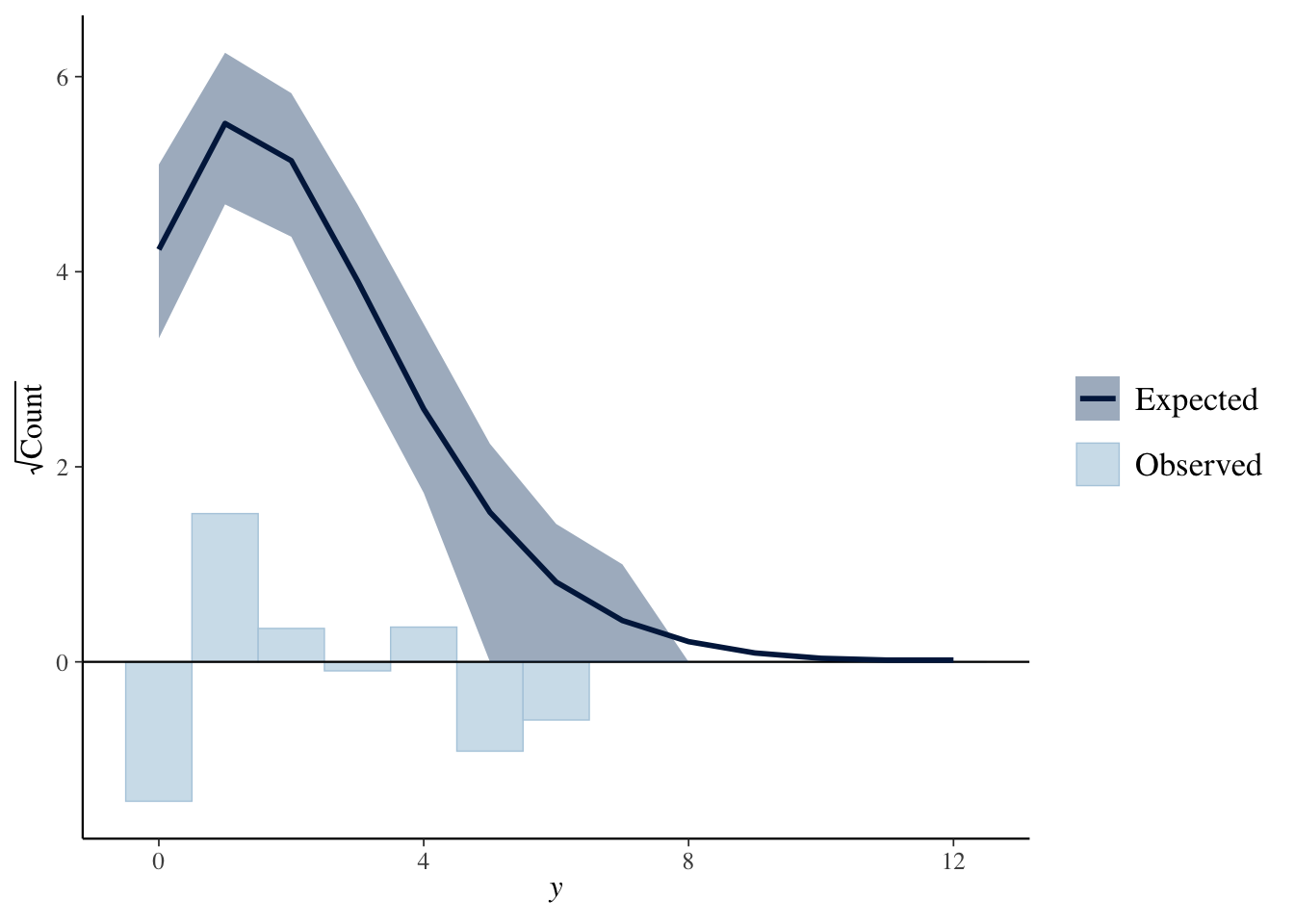
やはり、複製データは0と1のあたりでズレが大きいようです。
モデル2
つづいて、ゼロ過剰ポアソン分布のモデルをあてはめます。
code2 <- nimbleCode({
for (n in 1:N) {
z[n] ~ dbern(p)
Y[n] ~ dpois(z[n] * lambda)
# replicated data
zrep[n] ~ dbern(p)
yrep[n] ~ dpois(zrep[n] * lambda)
}
# prior
p ~ dunif(0, 1)
lambda ~ dunif(0, 100)
})あてはめ
init_fun2 <- function() {
list(p = runif(1, 0, 1),
lambda = runif(1, 0, 2),
z = rep(1, N),
zrep = rep(1, N),
yrep = rpois(N, 1))
}
fit2 <- nimbleMCMC(code = code2,
constants = list(N = N),
data = list(Y = Y),
inits = init_fun2,
monitors = c("p", "lambda", "yrep"),
nchains = 3,
niter = 2000, nburnin = 1000,
samplesAsCodaMCMC = TRUE)
## Defining model
## Building model
## Setting data and initial values
## Running calculate on model
## [Note] Any error reports that follow may simply reflect missing values in model variables.
## Checking model sizes and dimensions
## Checking model calculations
## Compiling
## [Note] This may take a minute.
## [Note] Use 'showCompilerOutput = TRUE' to see C++ compilation details.
## running chain 1...
## |-------------|-------------|-------------|-------------|
## |-------------------------------------------------------|
## running chain 2...
## |-------------|-------------|-------------|-------------|
## |-------------------------------------------------------|
## running chain 3...
## |-------------|-------------|-------------|-------------|
## |-------------------------------------------------------|パラメータlambdaとpについて結果の要約をみます。
fit2 |>
as_draws() |>
summarise_draws() |>
filter(variable %in% c("p", "lambda"))
## # A tibble: 2 × 10
## variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
## <chr> <num> <num> <num> <num> <num> <num> <num> <num> <num>
## 1 lambda 2.27 2.26 0.196 0.188 1.96 2.61 1.00 457. 570.
## 2 p 0.758 0.759 0.0564 0.0569 0.667 0.854 1.01 307. 305.事後予測検査
モデル1のときと同様に、複製データyrepのMCMCサンプルを取り出して、yrep2に入れておきます。
yrep2 <- fit2 |>
as_draws_df() |>
select(starts_with("yrep")) |>
as_draws_matrix()以下は、モデル1のときと同様です。
ppc_bars
複製データyrep2と観測値Yの分布を比較します。
ppc_bars(Y, yrep2)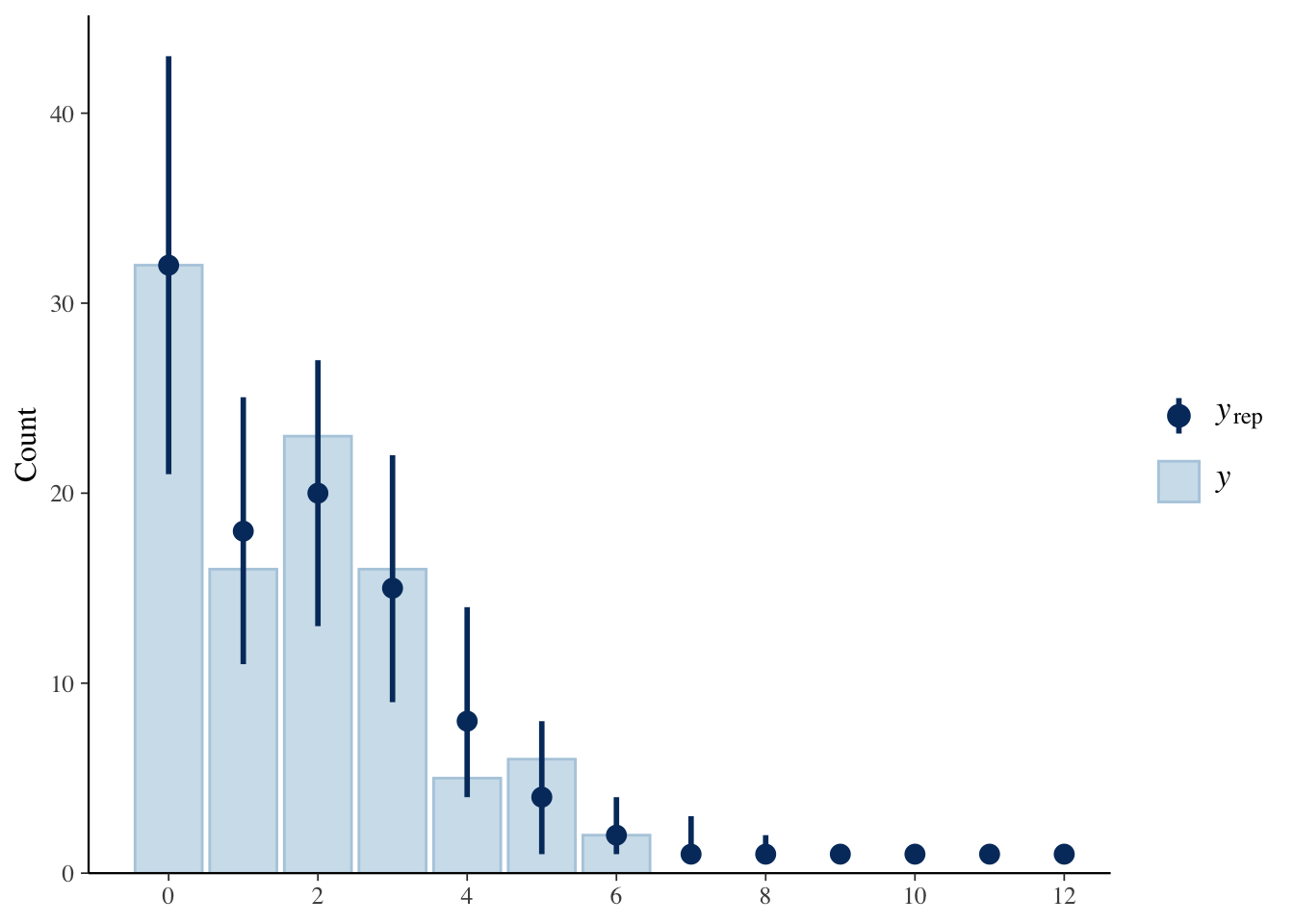
ppc_rootogram
Rootgramでの比較です。
ppc_rootogram(Y, yrep2, style = "standing")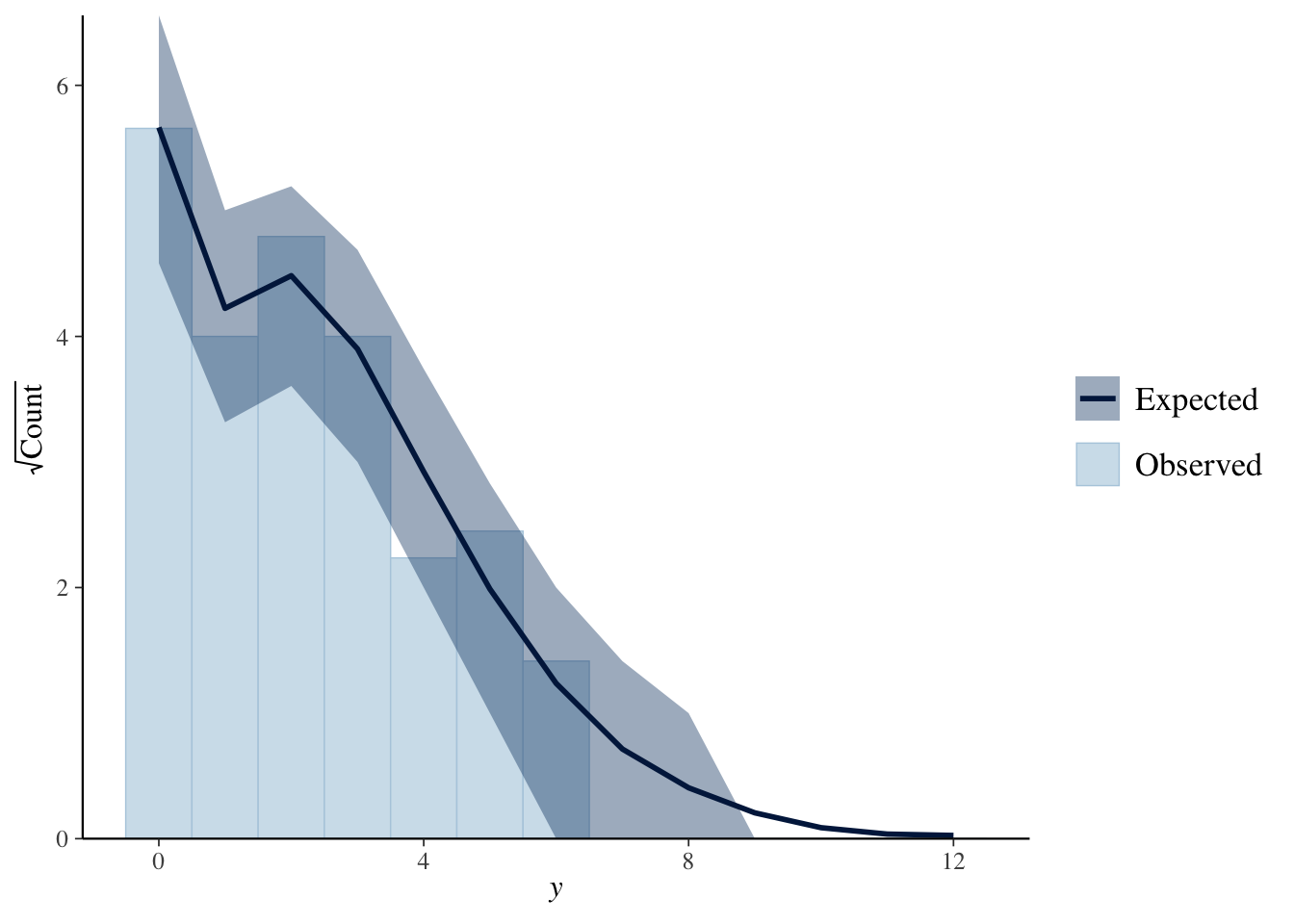
ppc_rootogram(Y, yrep2, style = "hanging")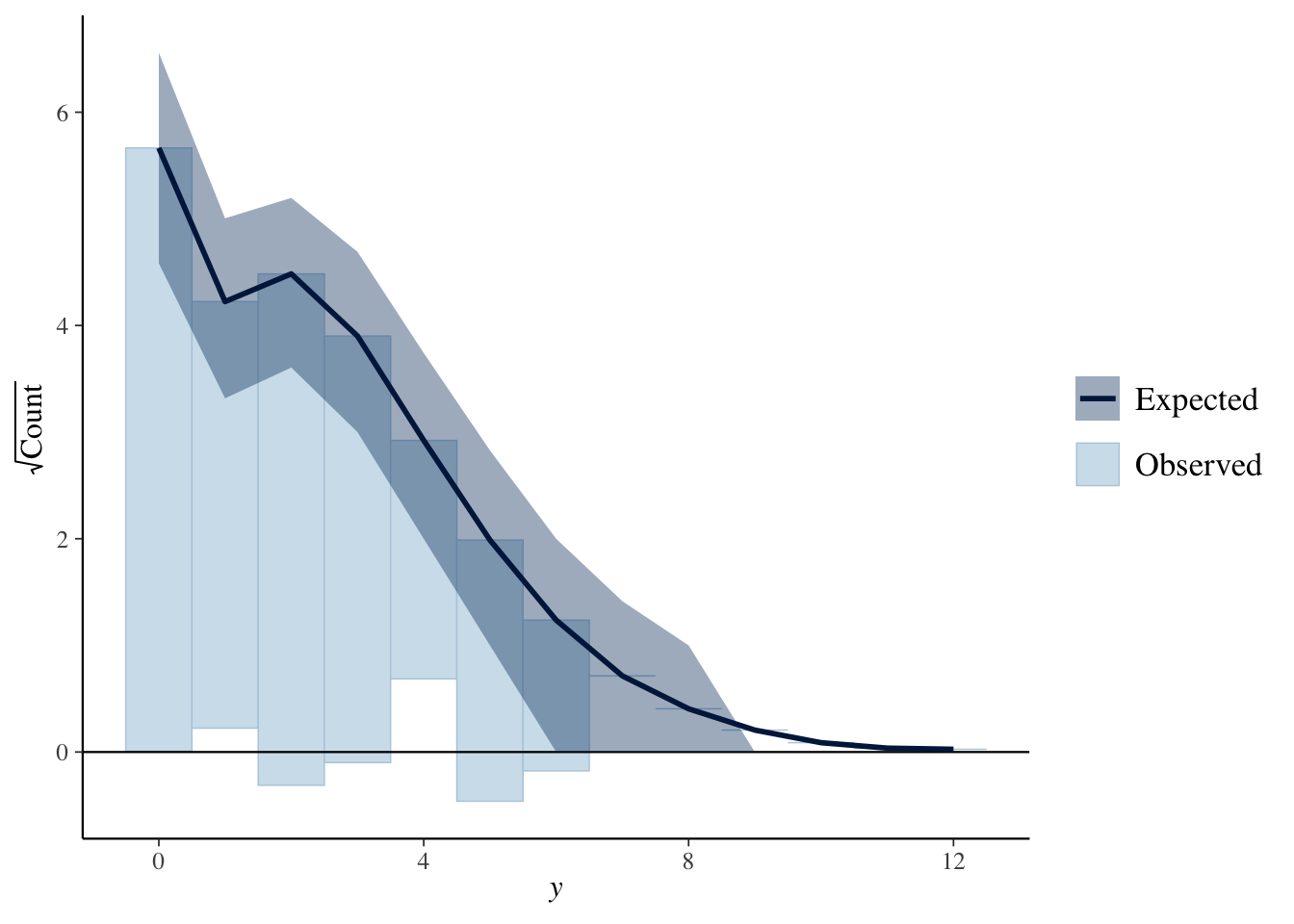
ppc_rootogram(Y, yrep2, style = "suspended")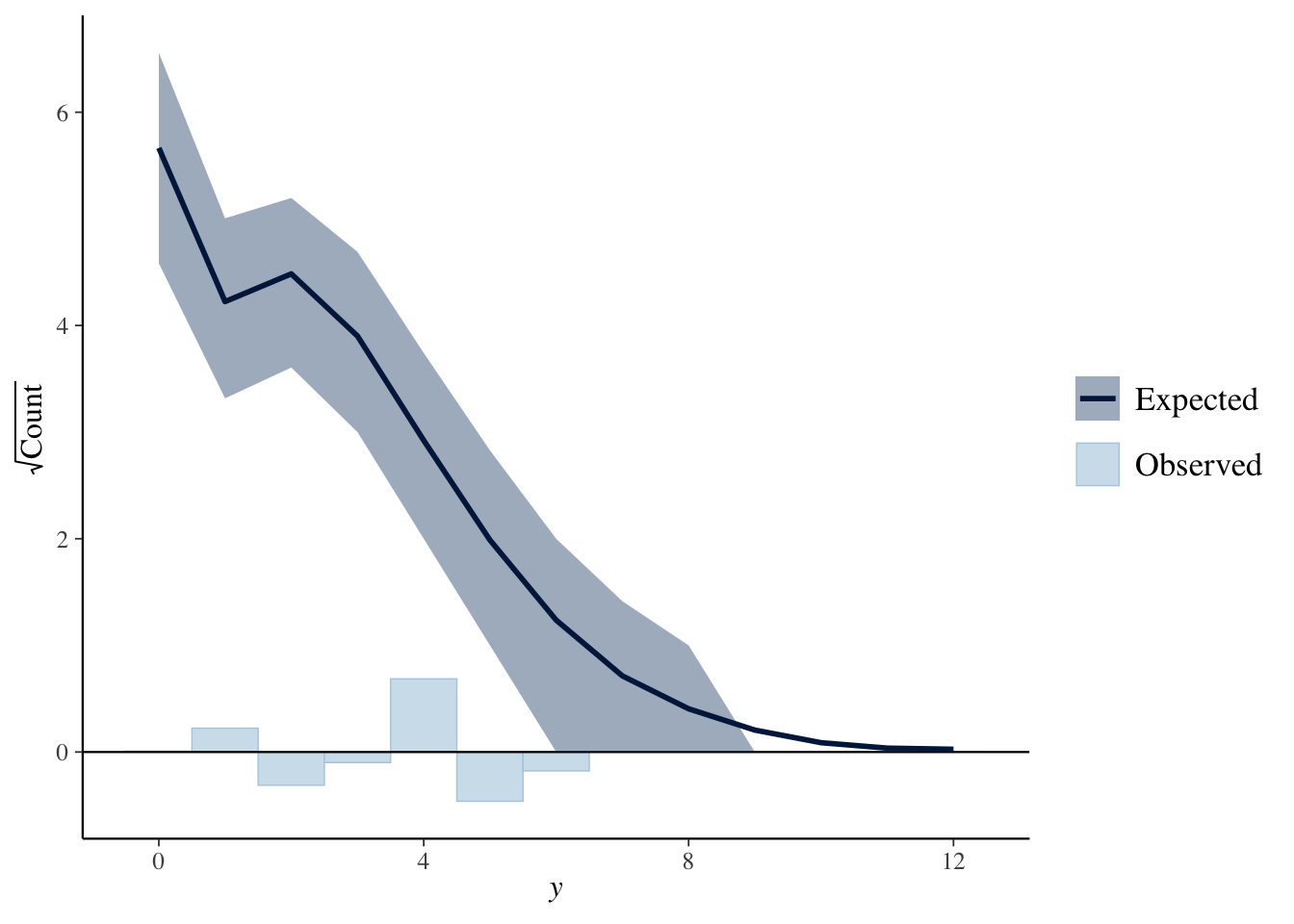
こちらは、複製データが観測値にあっているようです(そのようにつくったからですが)。
おわりに
以上のように、bayesplotパッケージの事後予測検査関数により、モデルのあてはまりを視覚的にチェックすることができます。
bayesplotパッケージ中の離散値データの事後予測検査関数の詳細については
PPCs for discrete outcomesをご覧ください。