ggplot2で第2種の誤りの確率を図示する

よくある図ですが、第2種の誤りの確率をggplot2で描いてみました。設定は、『統計学実践ワークブック』の第10章を参考にしています。

設定1

帰無仮説H₀では平均が1であるとし、対立仮説H₁は平均が2であるとします。分散は4、標本サイズnは10とします。

H₀が正しいとき、統計検定量\(Z_{0}=\frac{\bar{X}-\mu_{0}}{\sqrt{\frac{\sigma^2}{n}}}\)は\(N(0,1)\)にしたがいます。H₁が正しいときには、\(Z_{0}\)は\(N\left(\frac{\mu_1 - \mu_0}{\sqrt{\frac{\sigma^2}{n}}},1\right)\)にしたがいます。

危険率5％で片側検定するばあいを考えます。

準備

パッケージを読み込んで、変数を設定します。

library(ggplot2)

n <- 10
sigma <- sqrt(4)
mu_h0 <- 1
mu_h1 <- 2
mu_Z <- (mu_h1 - mu_h0) / (sigma / sqrt(n))

# 95% limit of N(0, 1)
upper_h0 <- qnorm(0.95, mean = 0, sd = 1)

図を描く関数を定義します。

plot_type2 <- function(mu_Z, limit, x_min = -5, x_max = 10) {
  ggplot() +
    stat_function(fun = dnorm, args = list(mean = 0, sd = 1),
                  geom = "line", colour = "blue") +
    stat_function(fun = dnorm, args = list(mean = 0, sd = 1),
                  geom = "area", fill = "blue", xlim = c(limit, x_max),
                  alpha = 0.5) +
    stat_function(fun = dnorm, args = list(mean = mu_Z, sd = 1),
                  geom = "line", colour = "red") +
    stat_function(fun = dnorm, args = list(mean = mu_Z, sd = 1),
                  geom = "area", fill = "red", xlim = c(x_min, limit),
                  alpha = 0.5) +
    scale_x_continuous(name = "Z", limits = c(x_min, x_max)) + 
    scale_y_continuous(name = "")
}

図の青く塗った領域の面積が第1種の誤りの確率(=0.05)、赤く塗った領域の面積が第2種の誤りの確率

plot_type2(mu_Z, upper_h0)

第2種の誤りの確率は以下のようになります。

pnorm(upper_h0, mean = mu_Z, sd = 1)
## [1] 0.5254013

設定2

標本サイズが100だと以下のようになります。

n2 <- 100
mu_Z2 <- (mu_h1 - mu_h0) / (sigma / sqrt(n2))

plot_type2(mu_Z2, upper_h0)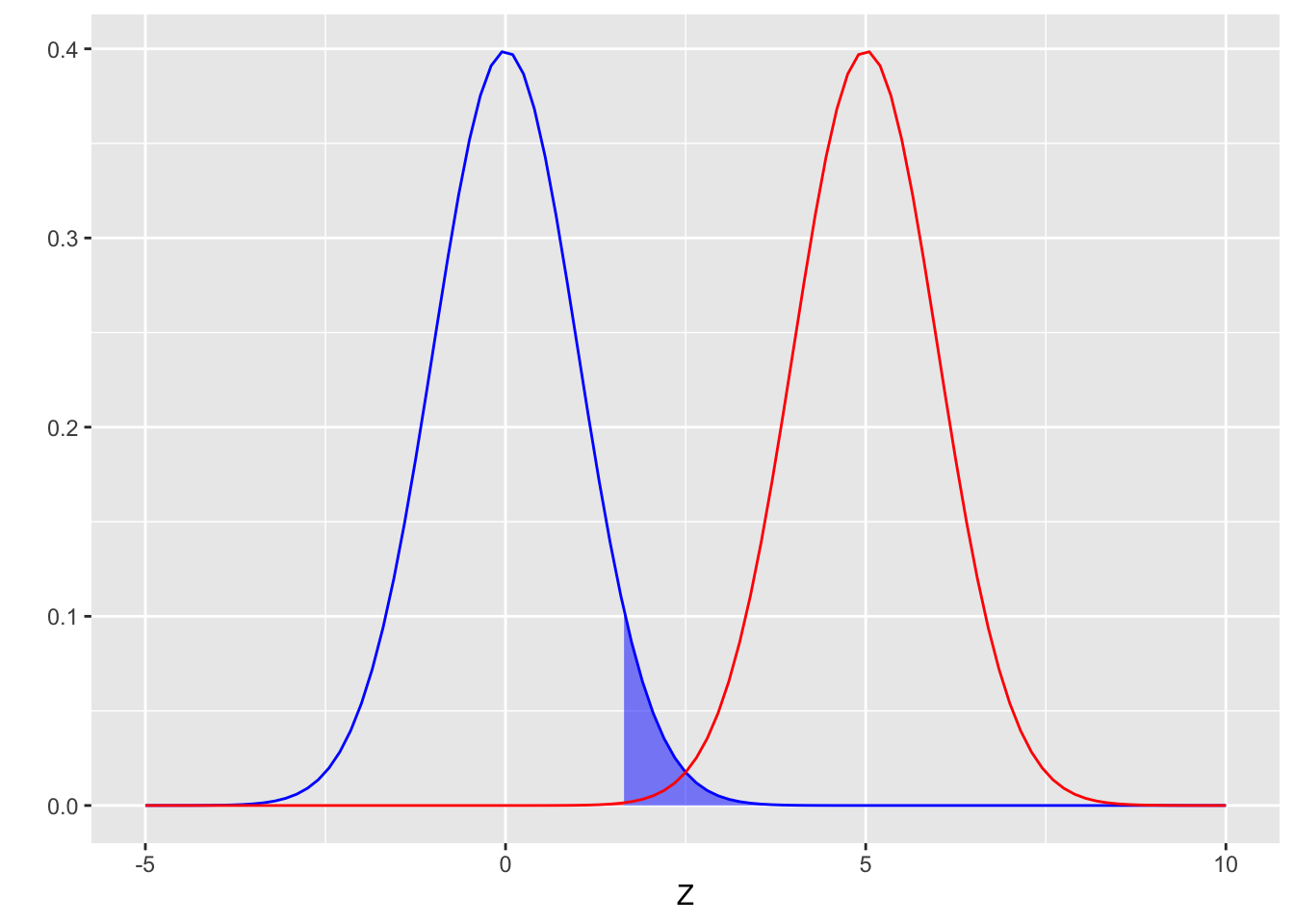

第2種の誤りの確率は以下のようになります。ほぼ0です。

pnorm(upper_h0, mean = mu_Z2, sd = 1)
## [1] 0.000396615