library(nimble)
## nimble version 1.3.0 is loaded.
## For more information on NIMBLE and a User Manual,
## please visit https://R-nimble.org.
##
## Note for advanced users who have written their own MCMC samplers:
## As of version 0.13.0, NIMBLE's protocol for handling posterior
## predictive nodes has changed in a way that could affect user-defined
## samplers in some situations. Please see Section 15.5.1 of the User Manual.
##
## 次のパッケージを付け加えます: 'nimble'
## 以下のオブジェクトは 'package:stats' からマスクされています:
##
## simulate
## 以下のオブジェクトは 'package:base' からマスクされています:
##
## declare
library(ggplot2)
library(posterior)
## This is posterior version 1.6.1
##
## 次のパッケージを付け加えます: 'posterior'
## 以下のオブジェクトは 'package:stats' からマスクされています:
##
## mad, sd, var
## 以下のオブジェクトは 'package:base' からマスクされています:
##
## %in%, match
set.seed(1234)
N <- 30
lambda <- c(1, 6, 12)
Y <- rpois(N * 3, rep(lambda, each = N))複数の個体群が混ざっている個体数データを想定して、平均が異なるポアソン分布が混合しているデータをディリクレ過程混合モデルでクラスター分けすることを考えてみます。
データ
ここでは、平均が1, 6, 12のポアソン分布にしたがう計測値が混ざっている個体数データを想定して、データを生成します。
以下のようなデータになりました。
ggplot(data.frame(Y = Y)) +
geom_bar(aes(x = Y))
NIMBLEモデル
NIMBLEによるモデルコードは以下のようになります。stick_breaking関数で折れ棒過程を使っています。
クラスタの数をKに格納するようにしています。
code <- nimbleCode({
for(n in 1:N) {
z[n] ~ dcat(pi[])
Y[n] ~ dpois(exp(phi[z[n]]))
}
for (m in 1:(M - 1)) {
q[m] ~ dbeta(1, alpha)
}
pi[1:M] <- stick_breaking(q[1:(M - 1)])
alpha ~ dgamma(1, 1)
for(m in 1:M) {
phi[m] ~ dnorm(0, sd = 10)
}
for (n in 1:N) {
for (m in 1:M) {
zind[n, m] <- equals(m, z[n])
}
}
for (m in 1:M) {
sumind[m] <- sum(zind[, m])
cl[m] <- step(sumind[m] - 1 + 0.001)
}
K <- sum(cl[])
})実行
定数、データ、初期値を定義して、サンプリングをおこないます。最後にposteriorパッケージのdraws型のオブジェクトにしています。
constants <- list(N = N * 3, M = 20)
data <- list(Y = Y)
inits <- list(z = sample(1:5, size = constants$N, replace = TRUE),
zind = matrix(0, ncol = constants$M, nrow = constants$N),
cl = rep(1, constants$M),
q = runif(constants$M, 0, 1),
pi = rep(1 / constants$M, constants$M),
phi = runif(constants$M, -2, 2),
alpha = 1)
samp <- nimbleMCMC(code, constants = constants,
data = data, inits = inits,
monitors = c("phi", "alpha", "pi", "K"),
nchains = 3,
niter = 10000, nburnin = 2000,
samplesAsCodaMCMC = TRUE) |>
as_draws()
## Defining model
## Building model
## Setting data and initial values
## Running calculate on model
## [Note] Any error reports that follow may simply reflect missing values in model variables.
## Checking model sizes and dimensions
## Checking model calculations
## Compiling
## [Note] This may take a minute.
## [Note] Use 'showCompilerOutput = TRUE' to see C++ compilation details.
## running chain 1...
## |-------------|-------------|-------------|-------------|
## |-------------------------------------------------------|
## running chain 2...
## |-------------|-------------|-------------|-------------|
## |-------------------------------------------------------|
## running chain 3...
## |-------------|-------------|-------------|-------------|
## |-------------------------------------------------------|結果
結果です。まずはalphaの事後分布の要約です。
summ <- samp |>
summary()
summ |>
dplyr::filter(variable == "alpha")
## # A tibble: 1 × 10
## variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 alpha 0.988 0.865 0.609 0.547 0.239 2.17 1.03 123. 209.クラスタ数Kの事後分布の要約です。
summ |>
dplyr::filter(startsWith(variable, "K"))
## # A tibble: 1 × 10
## variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 K 4.94 5 1.60 1.48 3 8 1.04 64.8 254.中央値は5、90%信用区間は3–8と推定されました。
カテゴリカル分布のパラメーターpiの事後分布の要約を図示します。
pi_est <- summ |>
dplyr::filter(startsWith(variable, "pi")) |>
dplyr::mutate(index = stringr::str_extract(variable, "[0-9]+") |>
as.numeric() |> as.factor())
ggplot(pi_est) +
geom_point(aes(x = index, y = mean)) +
geom_segment(aes(x = index, xend = index, y = q5, yend = q95)) +
labs(x = "Component", y = "Probability")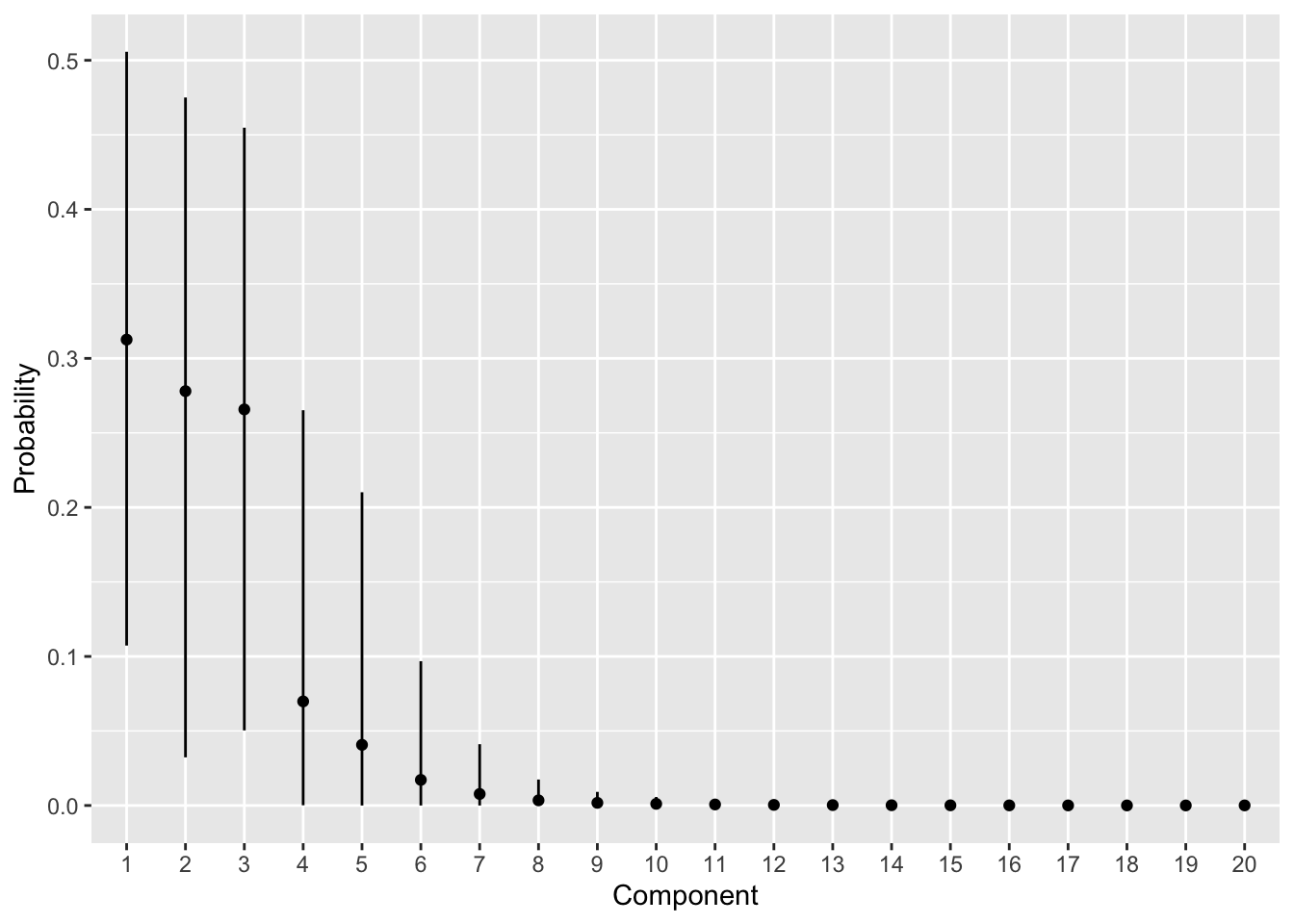
真のカテゴリー数は3ですが、そのあたりまでの確率が高くなっています。
各カテゴリーの平均の対数phiは、ラベルスイッチングが起きるので、そのままでは多峰になってしまいます。Stanだと、ordered_vector型で解決できそうなのですが、NIMBLEにはありません。dconstraintで、大小関係等の制約をかけることはできるのですが、この場合は引数の数が不定ですので、使えません。このあたりはもう少し考えてみます。
【追記】Stanでもやってみましたが、単純にordered vectorを使えばよいというものでもありませんでした。