library(TidyDensity)
##
## == Welcome to TidyDensity ===========================================================================
## If you find this package useful, please leave a star:
## https://github.com/spsanderson/TidyDensity'
##
## If you encounter a bug or want to request an enhancement please file an issue at:
## https://github.com/spsanderson/TidyDensity/issues
##
## Thank you for using TidyDensity!
library(ggplot2)
set.seed(123)TidyDensityというパッケージがありました。さまざまな確率分布に従う乱数をtidyな形で生成できるというもののようです。
つかってみる
TidyDensityパッケージはCRANからインストールできます。ドキュメントはhttps://www.spsanderson.com/TidyDensity/にあります。
平均10、標準偏差2の正規乱数を100個生成してみます。
d_norm <- tidy_normal(.n = 100, .mean = 20, .sd = 2)tibble形式でデータができるので、内容を確認してみます。
d_norm
## # A tibble: 100 × 7
## sim_number x y dx dy p q
## <fct> <int> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 1 1 18.9 13.5 0.0000717 0.288 18.9
## 2 1 2 19.5 13.6 0.000130 0.409 19.5
## 3 1 3 23.1 13.7 0.000227 0.940 23.1
## 4 1 4 20.1 13.9 0.000380 0.528 20.1
## 5 1 5 20.3 14.0 0.000612 0.551 20.3
## 6 1 6 23.4 14.1 0.000947 0.957 23.4
## 7 1 7 20.9 14.3 0.00141 0.678 20.9
## 8 1 8 17.5 14.4 0.00203 0.103 17.5
## 9 1 9 18.6 14.5 0.00281 0.246 18.6
## 10 1 10 19.1 14.6 0.00376 0.328 19.1
## # ℹ 90 more rows各列の内容は以下のようです。
sim_numberはシミュレーション番号(今回はデフォルトで.num_sims = 1となっているのですべて1)xは各シミュレーション中の連番(今回は1〜100)yは生成された乱数dxとdyはそれぞれ、生成された乱数(y)をstats::density関数に適用したときの返り値のxとypは、yを分布関数(pnorm)に適用したときの値qは、pを分位点関数(qnorm)に適用したときの値
しかし、yとqとは同じ値になるのではないかとか、同じ行のyとdyとは対応関係がないので、tidy dataの原則からは外れるのではないかという気もします。
グラフ表示
.num_sims = 4として、結果をtidy_four_autoplot関数でプロットしてみます。
tidy_normal(.n = 100, .mean = 20, .sd = 2, .num_sims = 4) |>
tidy_four_autoplot()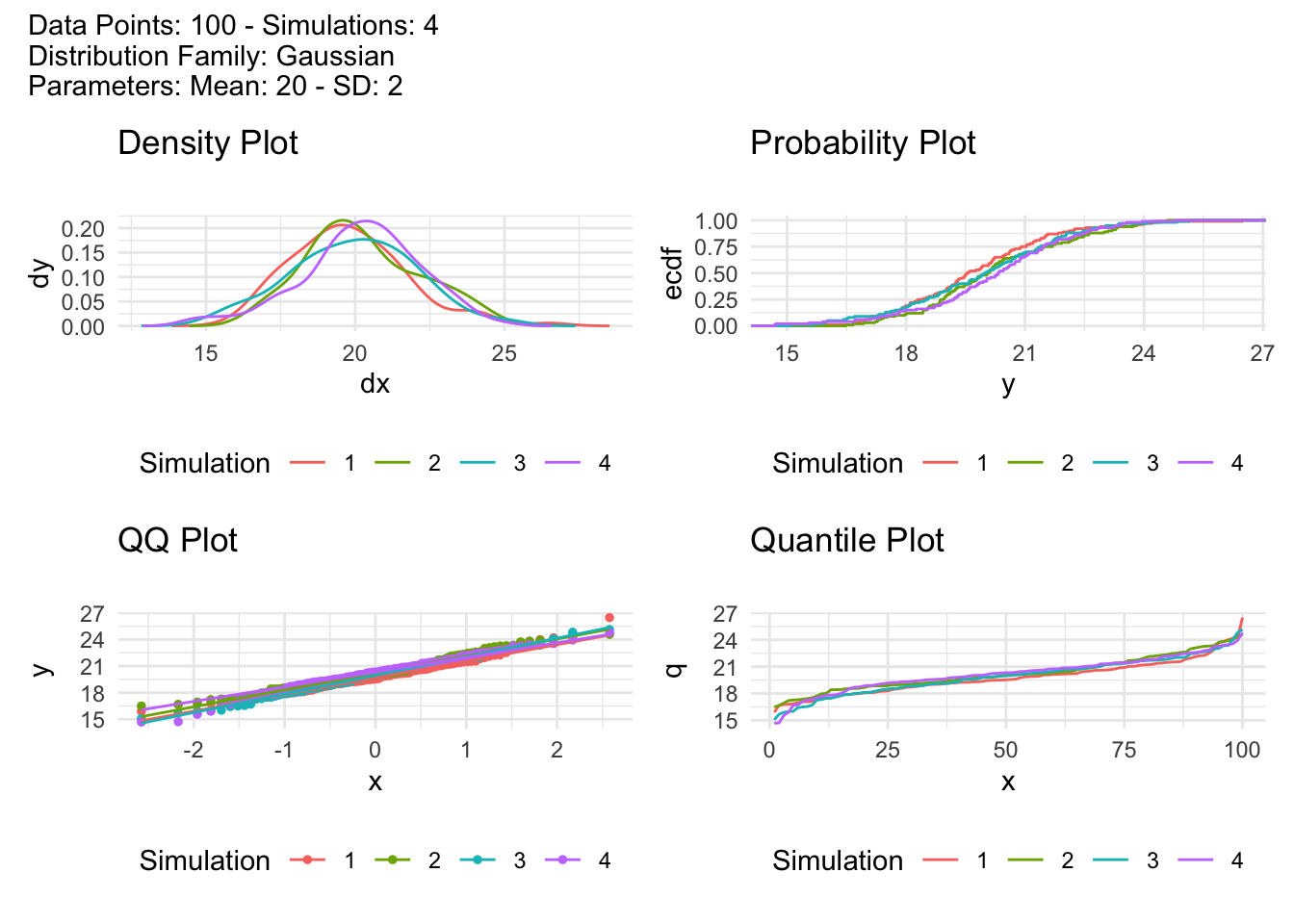
MCMC
マルコフ連鎖モンテカルロ(MCMC)のサンプリングもできるようです。
データとして平均3のポアソン分布にしたがう乱数を生成しました。
y <- tidy_poisson(25, .lambda = 3) |>
dplyr::pull(y)
print(y)
## [1] 2 3 1 5 5 3 4 2 1 3 3 2 1 3 0 4 3 3 3 2 3 4 3 2 4
mean(y)
## [1] 2.76このデータの平均を推定します。
fit <- tidy_mcmc_sampling(y, .fns = "mean", .cum_fns = "cmean",
.num_sims = 2000)mcmc_data要素にデータがtibble形式ではいっています。
head(fit$mcmc_data, 8)
## # A tibble: 8 × 3
## sim_number name value
## <fct> <fct> <dbl>
## 1 1 .sample_mean 2.75
## 2 1 .cum_stat_cmean 2.75
## 3 2 .sample_mean 2.55
## 4 2 .cum_stat_cmean 2.65
## 5 3 .sample_mean 2.7
## 6 3 .cum_stat_cmean 2.67
## 7 4 .sample_mean 2.65
## 8 4 .cum_stat_cmean 2.66plt要素にはプロットがはいっています。
fit$plt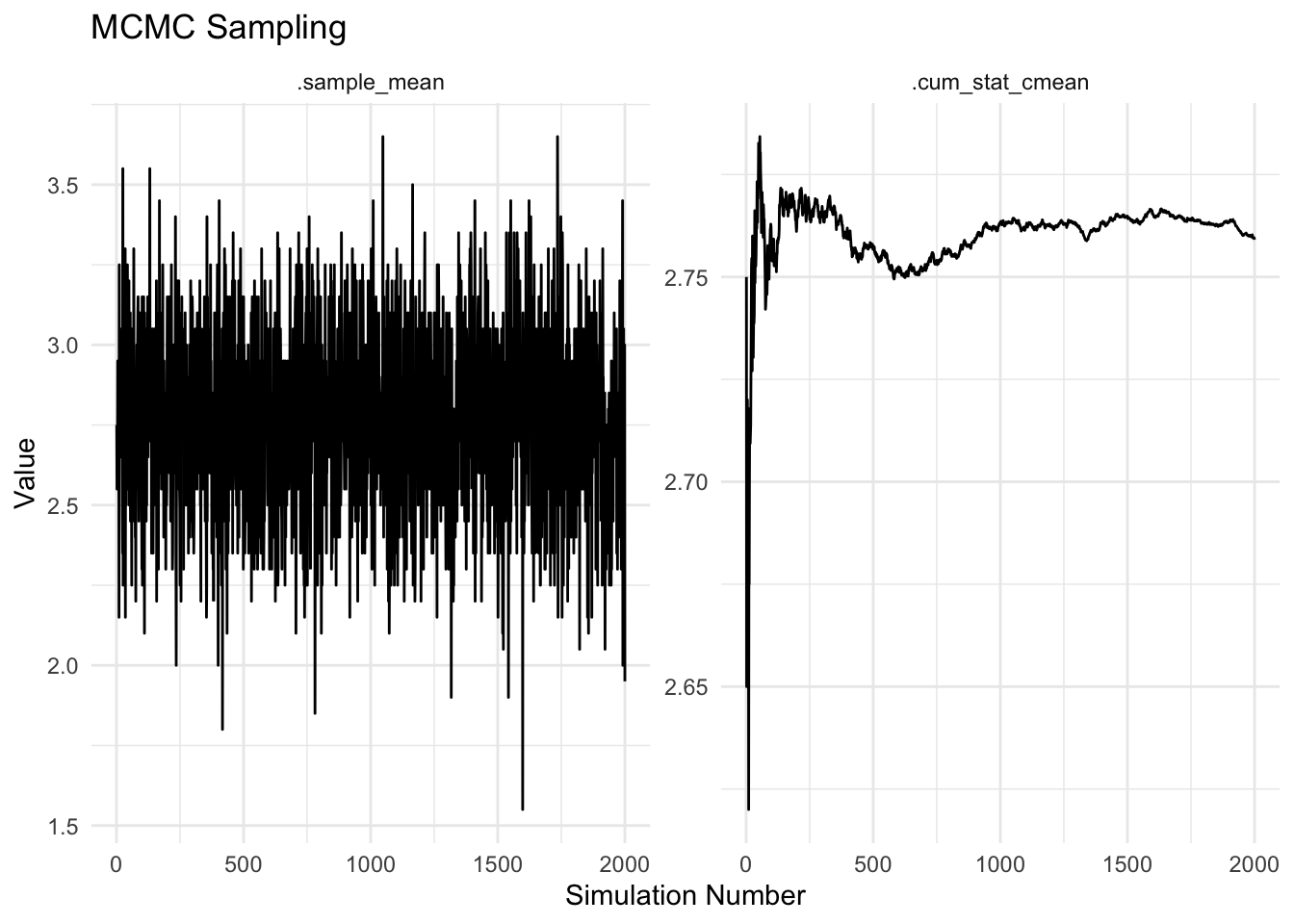
モンテカルロ積分
つぎにモンテカルロ積分をやってみました。
\(U\)を、区間(0, 1)の一様分布に従う確率変数として、
\[ E\left[\sqrt{1-U^2}\right]=\int_0^1\sqrt{1-u^2}du=\frac{\pi}{4} \]
を利用して円周率\(\pi\)を求めます。10000個の乱数による計算を8回くりかえしました。
tidy_uniform(10000, .min = 0, .max = 1, .num_sims = 8) |>
dplyr::mutate(z = sqrt(1 - y^2)) |>
dplyr::group_by(sim_number) |>
dplyr::summarise(pi = 4 * mean(z))
## # A tibble: 8 × 2
## sim_number pi
## <fct> <dbl>
## 1 1 3.14
## 2 2 3.15
## 3 3 3.14
## 4 4 3.13
## 5 5 3.14
## 6 6 3.13
## 7 7 3.14
## 8 8 3.14