library(TMB)
library(ggplot2)
set.seed(123)TMBで、状態空間モデルのあてはめをやってみました。ただ、モデル式をそのままコード化したものでは、最適化計算がうまく収束しませんでした。
【追記】「TMBを活用して、状態空間モデルをラプラス近似により高速に推定する | Logics of Blue」にうまく収束した例があります。どこが違うかというと、MakeAdFun関数の引数にrandom = "alpha" を加える必要があったのでした。
準備
いつものように、TMBとggplot2を読み込みます。擬似乱数も固定します。
データ
ナイル川のデータを使用します。今回は、数値計算が安定するように流量の値を1000で割っておきました。元の値の単位が 108 m3 なので、変換後は 1011 m3 ということになります。また、tsクラスのデータをデータフレームに変換しておきました。
Nile_df <- data.frame(Year = 1871:1970,
Y = c(Nile) / 1000)
p <- ggplot(Nile_df, aes(x = Year, y = Y)) +
geom_line()
plot(p)
モデル
状態空間モデルにあてはめます。ここでは1回差分で線形正規のローカルレベルモデルとします。
システムモデル
\[ \alpha_{t} = \alpha_{t-1} + \eta_{t}, \quad \eta_{t} \sim N(0, \sigma_{\eta}^2) \]
観測モデル
\[ Y_{t} = \alpha_{t} + \epsilon_{t}, \quad \epsilon_{t} \sim N(0, \sigma_{\epsilon}^2) \]
ローカルレベルモデルをTMBで記述します。まずは上のモデル式をそのままコードにしてみました。
ssm1.cpp
// State space model
#include <TMB.hpp>
template<class Type>
Type objective_function<Type>::operator() ()
{
DATA_VECTOR(Y);
DATA_SCALAR(m0);
DATA_SCALAR(C0);
PARAMETER_VECTOR(alpha);
PARAMETER(log_sigma_eta);
PARAMETER(log_sigma_eps);
int n = Y.size();
Type ll = dnorm(alpha(0), m0, sqrt(C0), true);
for (int t = 1; t < n; t++) {
ll += dnorm(alpha(t), alpha(t - 1), exp(log_sigma_eta), true);
}
for (int t = 0; t < n; t++) {
ll += dnorm(Y(t), alpha(t), exp(log_sigma_eps), true);
}
return -ll;
}コンパイルと最適化
モデルをコンパイルして、できたライブラリをロードします。
model_name <- "ssm1"
file.path("models", paste(model_name, "cpp", sep = ".")) |>
compile()
## Note: Using Makevars in /Users/hiroki/.R/Makevars
## using C++ compiler: 'Apple clang version 17.0.0 (clang-1700.3.19.1)'
## using SDK: ''
## [1] 0
file.path("models", dynlib(model_name)) |>
dyn.load()データと、パラメータの初期値を用意して最適化を実行します。
しかし、このモデルでは収束しませんでした。nlminb関数のeval.maxとiter.maxを増やしてもダメでした。
【追記】最初の追記で述べたように、ここで、MakeAdFun関数の引数にrandom = "alpha" を加える必要がありました。こうすると計算がうまく収束しました。
data <- list(Y = Nile_df$Y, m0 = 0, C0 = 1000)
parameters <- list(alpha = rep(1, nrow(Nile_df)),
log_sigma_eta = 0,
log_sigma_eps = 0)
obj <- MakeADFun(data, parameters, DLL = model_name)
opt <- nlminb(obj$par, obj$fn, obj$gr,
control = list(eval.max = 100,
iter.max = 100))結果です。convergenceが1なので、収束していません。messageにも出ていますが。
print(opt)
## $par
## alpha alpha alpha alpha alpha
## 1.0677169 1.0673157 1.0666821 1.0662118 1.0651758
## alpha alpha alpha alpha alpha
## 1.0635592 1.0619342 1.0602309 1.0585951 1.0557058
## alpha alpha alpha alpha alpha
## 1.0523299 1.0491020 1.0462711 1.0427704 1.0395511
## alpha alpha alpha alpha alpha
## 1.0361627 1.0327649 1.0289340 1.0256462 1.0222775
## alpha alpha alpha alpha alpha
## 1.0184435 1.0143659 1.0098995 1.0044455 0.9988440
## alpha alpha alpha alpha alpha
## 0.9923429 0.9850908 0.9779326 0.9701240 0.9629786
## alpha alpha alpha alpha alpha
## 0.9563019 0.9495046 0.9433231 0.9374785 0.9318846
## alpha alpha alpha alpha alpha
## 0.9267077 0.9218265 0.9175848 0.9134062 0.9087132
## alpha alpha alpha alpha alpha
## 0.9041769 0.8996056 0.8957796 0.8932439 0.8908095
## alpha alpha alpha alpha alpha
## 0.8887567 0.8867447 0.8836058 0.8814222 0.8791589
## alpha alpha alpha alpha alpha
## 0.8773187 0.8757948 0.8745801 0.8732096 0.8720267
## alpha alpha alpha alpha alpha
## 0.8714135 0.8707897 0.8706811 0.8708152 0.8705659
## alpha alpha alpha alpha alpha
## 0.8702835 0.8707520 0.8709854 0.8712781 0.8715063
## alpha alpha alpha alpha alpha
## 0.8713424 0.8711903 0.8713660 0.8707772 0.8708092
## alpha alpha alpha alpha alpha
## 0.8710026 0.8720633 0.8727300 0.8738704 0.8752079
## alpha alpha alpha alpha alpha
## 0.8766028 0.8777318 0.8786572 0.8800693 0.8808317
## alpha alpha alpha alpha alpha
## 0.8818143 0.8831746 0.8846187 0.8864180 0.8871512
## alpha alpha alpha alpha alpha
## 0.8881416 0.8889625 0.8896293 0.8900972 0.8904886
## alpha alpha alpha alpha alpha
## 0.8907659 0.8907845 0.8907253 0.8899792 0.8894567
## alpha alpha alpha alpha alpha
## 0.8879432 0.8872327 0.8861510 0.8854612 0.8852800
## log_sigma_eta log_sigma_eps
## -5.1123217 -2.1532164
##
## $objective
## [1] -450.4888
##
## $convergence
## [1] 1
##
## $iterations
## [1] 88
##
## $evaluations
## function gradient
## 100 88
##
## $message
## [1] "function evaluation limit reached without convergence (9)"カルマンフィルタの尤度を使ったモデル
単純なコード化ではダメだったので、カルマンフィルタの尤度を使用することにしました。尤度の式は野村(2016)を参考にしました。最適化のためなら定数部分は省略してもよさそうですが、いちおうちゃんと尤度を計算するようにしています。
ssm2.cpp
// State space model using Kalman filter
#include <TMB.hpp>
template<class Type>
Type objective_function<Type>::operator() ()
{
DATA_VECTOR(Y);
DATA_SCALAR(a0);
DATA_SCALAR(P0);
PARAMETER(log_sigma_eta);
PARAMETER(log_sigma_eps);
int n = Y.size();
vector<Type> P(n);
vector<Type> F(n);
vector<Type> K(n);
vector<Type> L(n);
vector<Type> a(n);
vector<Type> v(n);
Type ll = -n / 2.0 * log(2.0 * M_PI);
P(0) = P0;
a(0) = a0;
for (int t = 0; t < n; t++) {
v(t) = Y(t) - a(t);
F(t) = P(t) + pow(exp(log_sigma_eps), 2.0);
K(t) = P(t) / F(t);
L(t) = 1.0 - K(t);
if (t < n - 1) {
P(t + 1) = P(t) * L(t) + pow(exp(log_sigma_eta), 2.0);
a(t + 1) = a(t) + K(t) * v(t);
}
ll += - 0.5 * (log(F(t)) + pow(v[t], 2.0) / F(t));
}
return -ll;
}コンパイルと最適化
モデルをコンパイルして、できたライブラリをロードします。
model_name <- "ssm2"
file.path("models", paste(model_name, "cpp", sep = ".")) |>
compile()
file.path("models", dynlib(model_name)) |>
dyn.load()データと、パラメータ(システムモデルと観測モデルの誤差の標準偏差の対数)の初期値を用意して最適化を実行します。
data <- list(Y = Nile_df$Y, a0 = 0, P0 = 1000)
parameters <- list(log_sigma_eta = 1,
log_sigma_eps = 1)
obj <- MakeADFun(data, parameters, DLL = model_name)
opt <- nlminb(obj$par, obj$fn, obj$gr)
## outer mgc: 54.811
## outer mgc: 47.67067
## outer mgc: 30.13291
## outer mgc: 9.976196
## outer mgc: 4.905411
## outer mgc: 5.577532
## outer mgc: 2.403372
## outer mgc: 0.5632631
## outer mgc: 0.5531079
## outer mgc: 0.1161105
## outer mgc: 0.0002061353
## outer mgc: 3.300339e-06結果です。こちらはうまく収束しました。
print(opt)
## $par
## log_sigma_eta log_sigma_eps
## -3.261528 -2.096579
##
## $objective
## [1] -46.94871
##
## $convergence
## [1] 0
##
## $iterations
## [1] 11
##
## $evaluations
## function gradient
## 18 12
##
## $message
## [1] "relative convergence (4)"DLM
比較のため、DLMパッケージを使用して、システムモデルと観測モデルの誤差分散の最尤推定をやってみました。
library(dlm)
##
## Attaching package: 'dlm'
## The following object is masked from 'package:ggplot2':
##
## %+%
buildFun <- function(x) {
dlmModPoly(order = 1, dV = exp(x[1]), dW = exp(x[2]),
m0 = 0, C0 = 1000)
}
fit <- dlmMLE(Nile_df$Y, parm = c(0, 0), buildFun)
dlmNile <- buildFun(fit$par)結果です。V(dlmNile)が観測モデルの誤差分散、W(dlmNile)がシステムモデルの誤差分散になります。
V(dlmNile)
## [,1]
## [1,] 0.01509853
W(dlmNile)
## [,1]
## [1,] 0.001469168先ほどのTMBの結果を比較してみます。dlmの結果とほぼ同じでした。
exp(opt$par["log_sigma_eps"])^2
## log_sigma_eps
## 0.01509853
exp(opt$par["log_sigma_eta"])^2
## log_sigma_eta
## 0.001469171平滑化曲線
TMBで推定された誤差標準偏差の値を使ってdlmで平滑化した値を求め、グラフにしました。
dlm2 <- buildFun(c(2 * opt$par["log_sigma_eps"],
2 * opt$par["log_sigma_eta"]))
smoothed <- dlmSmooth(Nile_df$Y, dlm2)
data.frame(Year = 1871:1970,
Y = Nile_df$Y,
theta = dropFirst(smoothed$s)) |>
ggplot() +
geom_line(aes(x = Year, y = Y)) +
geom_line(aes(x = Year, y = theta), colour = "red")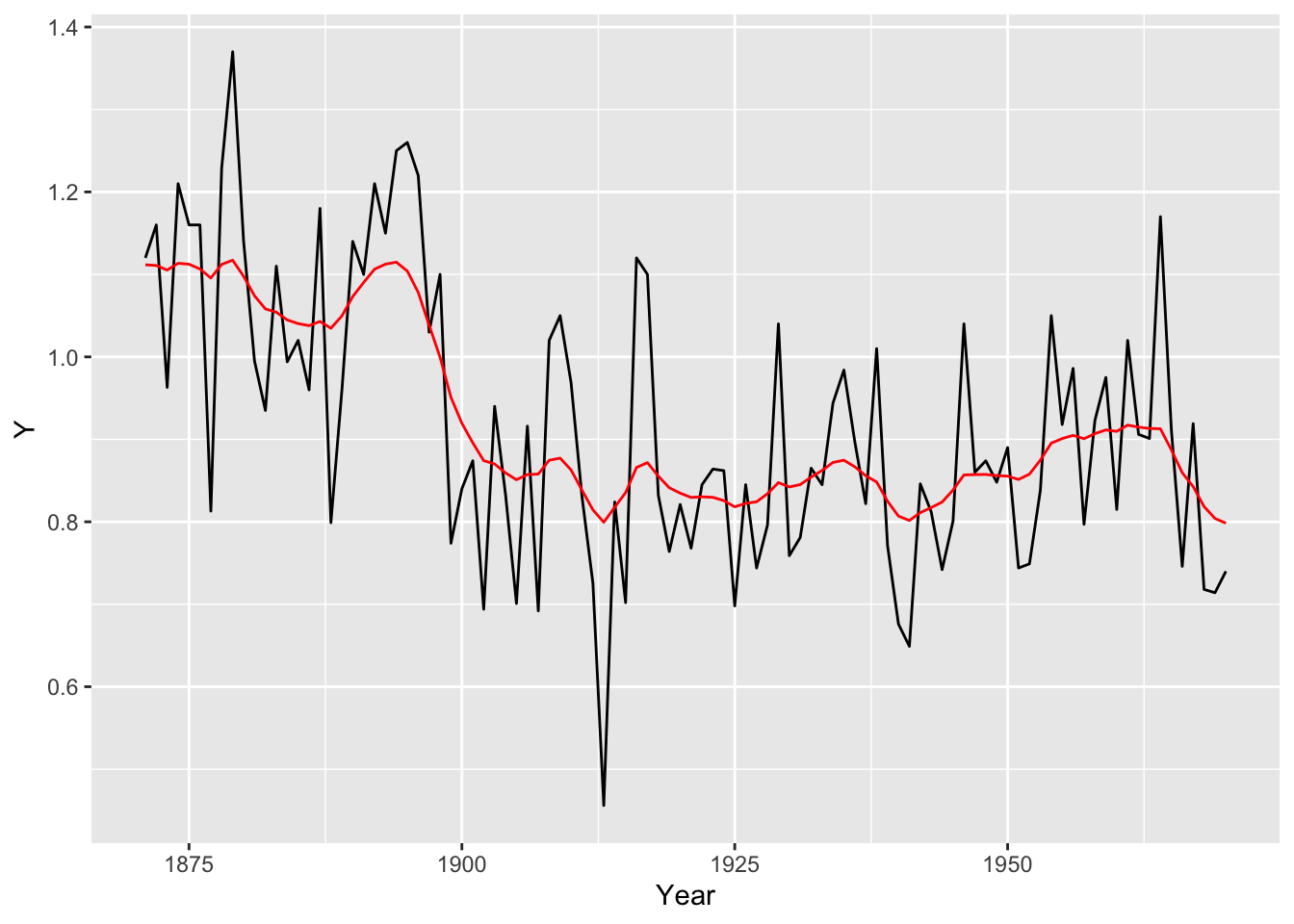
参考文献
- 野村俊一 (2016) カルマンフィルタ—Rを使った時系列予測と状態空間モデル—. 共立出版, 154pp.