Rにおける順序尺度の説明変数の扱い

R
作者

伊東宏樹

公開

2025年2月20日

Rでは順序尺度の説明変数がどのように扱われるか、についてのメモです。

例

以下のようなデータを用意します。説明変数はA, B, C, Dの4水準の因子型で、x0は名義尺度、x1は順序尺度とします。目的変数yは、A, B, C, Dに対してそれぞれ平均2, 2.5, 5, 5,5の値を取るとします。

set.seed(1234)

lv <- c("A", "B", "C", "D")
rp <- 10
x <- rep(lv, each = rp)
x0 <- factor(x, ordered = FALSE)
x1 <- factor(x, ordered = TRUE)
y <- rep(c(2, 2.5, 5, 5.5), each = rp) + rnorm(length(x), 0, 0.5)

x0とx1を表示します。x1の方は”Levels: A < B < C < D“と表示されます。

print(x0)
##  [1] A A A A A A A A A A B B B B B B B B B B C C C C C C C C C C D D D D D D D D
## [39] D D
## Levels: A B C D
print(x1)
##  [1] A A A A A A A A A A B B B B B B B B B B C C C C C C C C C C D D D D D D D D
## [39] D D
## Levels: A < B < C < D

データを図示します。

library(ggplot2)

data.frame(x = x0, y = y) |>
  ggplot(aes(x = x, y = y)) +
  geom_violin() +
  geom_point()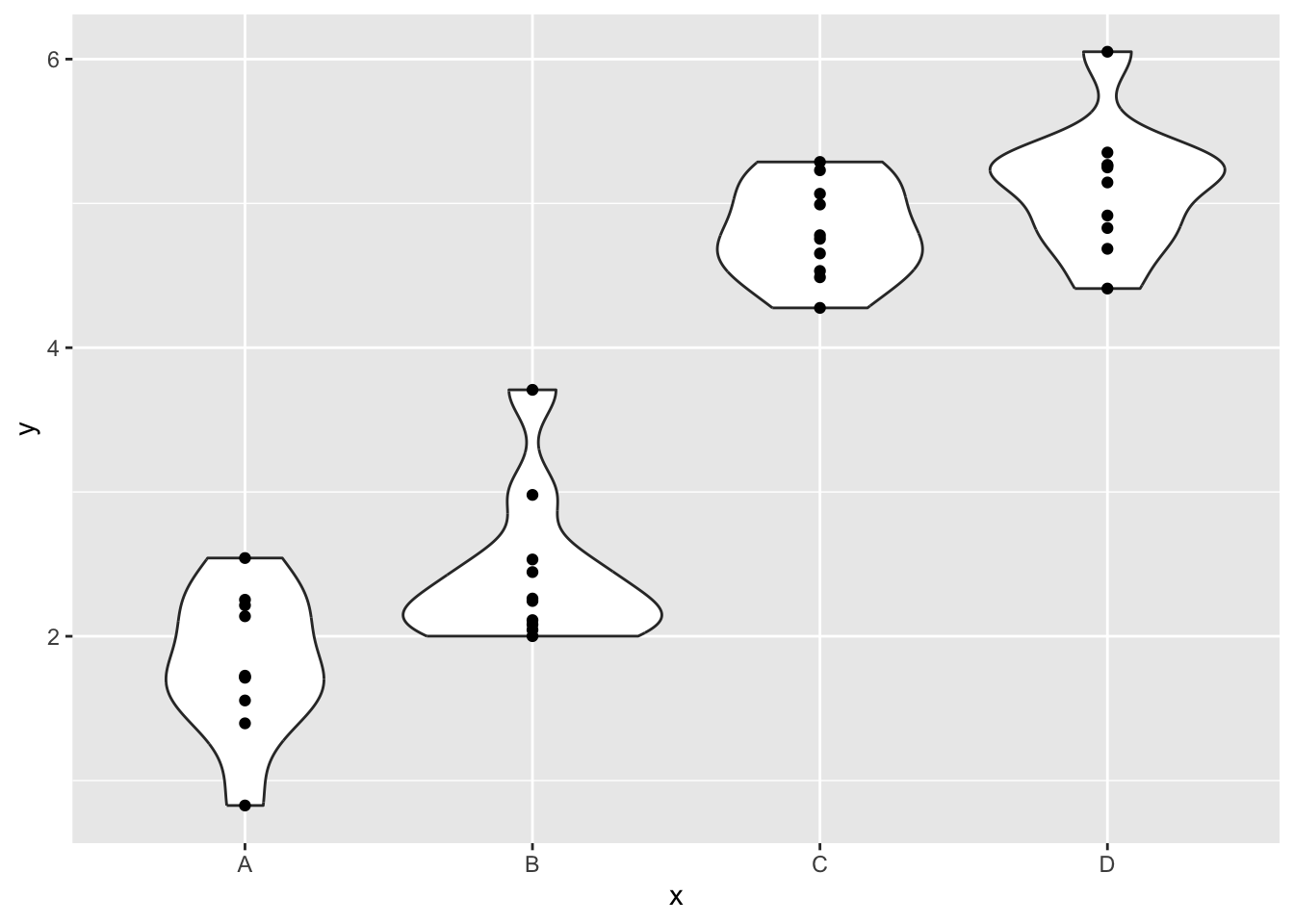

あてはめ

線形モデルにあてはめます。通常の因子型（名義尺度）のx0では、水準B, C, Dがダミー変数となります。

summary(lm(y ~ x0))
## 
## Call:
## lm(formula = y ~ x0)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.98127 -0.29501 -0.06655  0.24222  1.26700 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   1.8084     0.1452   12.45  1.3e-14 ***
## x0B           0.6325     0.2054    3.08  0.00395 ** 
## x0C           2.9976     0.2054   14.60  < 2e-16 ***
## x0D           3.3085     0.2054   16.11  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4592 on 36 degrees of freedom
## Multiple R-squared:  0.9162, Adjusted R-squared:  0.9092 
## F-statistic: 131.1 on 3 and 36 DF,  p-value: < 2.2e-16

順序尺度のx1では以下のようになります。

summary(lm(y ~ x1))
## 
## Call:
## lm(formula = y ~ x1)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.98127 -0.29501 -0.06655  0.24222  1.26700 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  3.54307    0.07261  48.797  < 2e-16 ***
## x1.L         2.74825    0.14522  18.925  < 2e-16 ***
## x1.Q        -0.16081    0.14522  -1.107    0.275    
## x1.C        -0.84677    0.14522  -5.831 1.17e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4592 on 36 degrees of freedom
## Multiple R-squared:  0.9162, Adjusted R-squared:  0.9092 
## F-statistic: 131.1 on 3 and 36 DF,  p-value: < 2.2e-16

x1.L, x1.Q, x1.Cというものが説明変数のところにあらわれましたが、これらの効果として表示される値は粕谷先生によると対比とのことです（［統計］［R］順序尺度の説明変数, 多項式対比）。

対比の係数となる対比行列はcontr.poly関数で求められて、4次の場合は以下のようになります。

contr.poly(4)
##              .L   .Q         .C
## [1,] -0.6708204  0.5 -0.2236068
## [2,] -0.2236068 -0.5  0.6708204
## [3,]  0.2236068 -0.5 -0.6708204
## [4,]  0.6708204  0.5  0.2236068

それぞれについてyとの関係をプロットしてみます。

apply(contr.poly(4), 2, rep, each = rp) |>
  data.frame() |>
  cbind(y) |>
  tidyr::pivot_longer(cols = `.L`:`.C`,
                      names_to = "var",
                      values_to = "x") |>
  dplyr::mutate(var = factor(var, levels = c(".L", ".Q", ".C"))) |>
  ggplot(aes(x = x, y = y)) +
  geom_point() +
  facet_wrap(~var)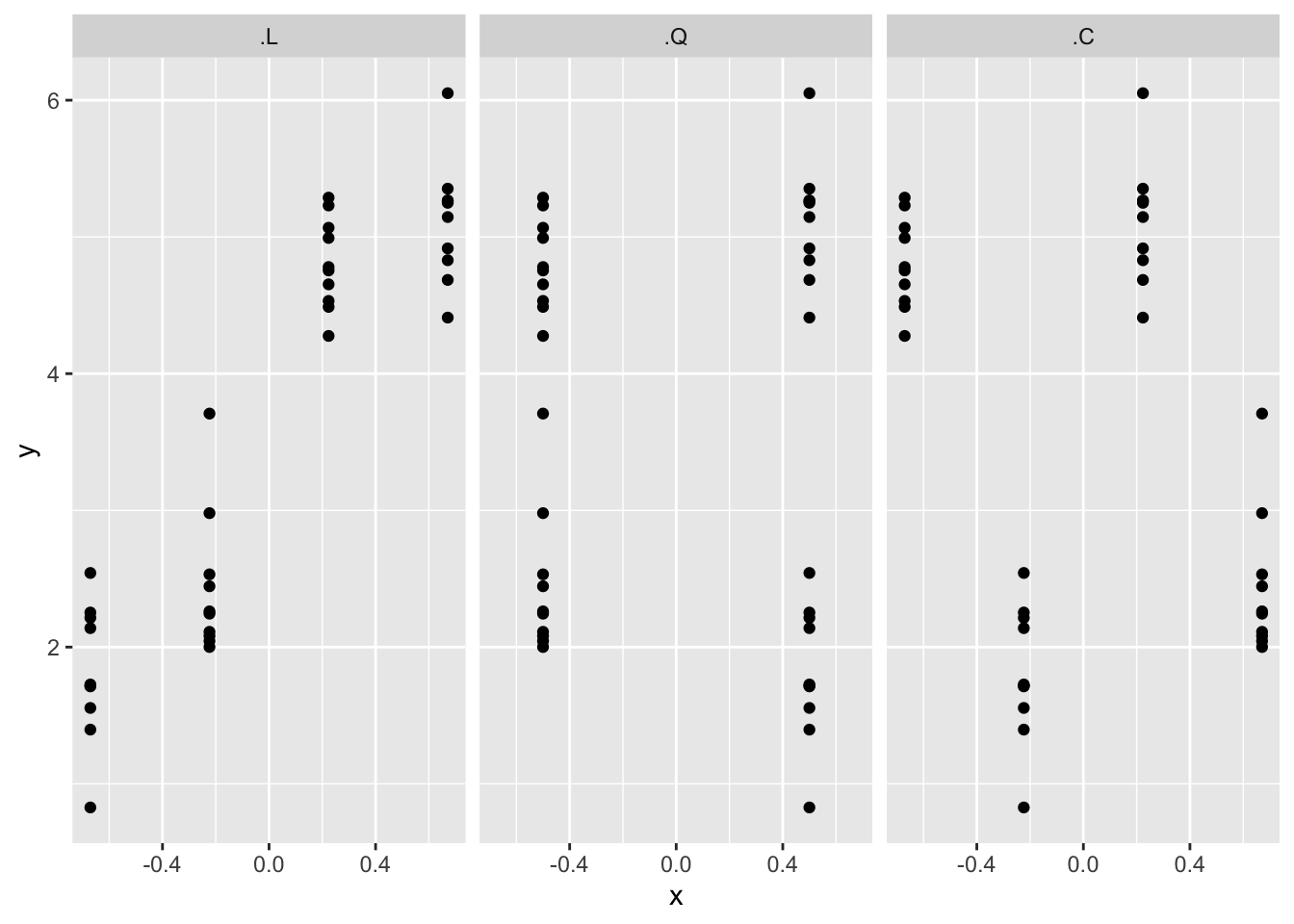

おわりに

粕谷先生もあまり釈然としないご様子ですが、やはりいまひとつすっきりしない感じです。