library(sem)豊田秀樹・前田忠彦・柳井晴夫『原因をさぐる統計学』(講談社ブルーバックス, 1992)の第3章にある、食物とガンとの関係を共分散構造分析(構造方程式モデリング)で解析する例をRのsemパッケージでやってみました。
元の本にはSASのCALISのプログラムが補章にありますが、lavaanパッケージを使用したRのスクリプト(とデータ)が特設ページで公開されています。
また、Stanによる実装が、StatModeling Memorandumの「SEMの多重指標モデルとMIMICモデル」にて公開されています。
準備
共分散構造分析のためにsemパッケージを読み込みます。
データ
特設ページからダウンロードした世界47カ国の食物とガンのデータ(本の図表2-5)のファイルCancer_raw.csvを読み込みます。
data <- readr::read_csv("data/Cancer_raw.csv")
## Rows: 47 Columns: 6
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## dbl (6): x1, x2, x3, x4, x5, x6
##
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.データの各変数は以下をあらわします。x1-x4は食物供給量(Cal/day)、x5-x6は男性のガンの部位別訂正死亡率(10万人対)です。
x1: 総熱量x2: 肉類x3: 乳製品x4: 酒類x5: 大腸ガンx6: 直腸ガン
散布図行列でデータを確認します。
GGally::ggpairs(data, progress = FALSE)
## Registered S3 method overwritten by 'GGally':
## method from
## +.gg ggplot2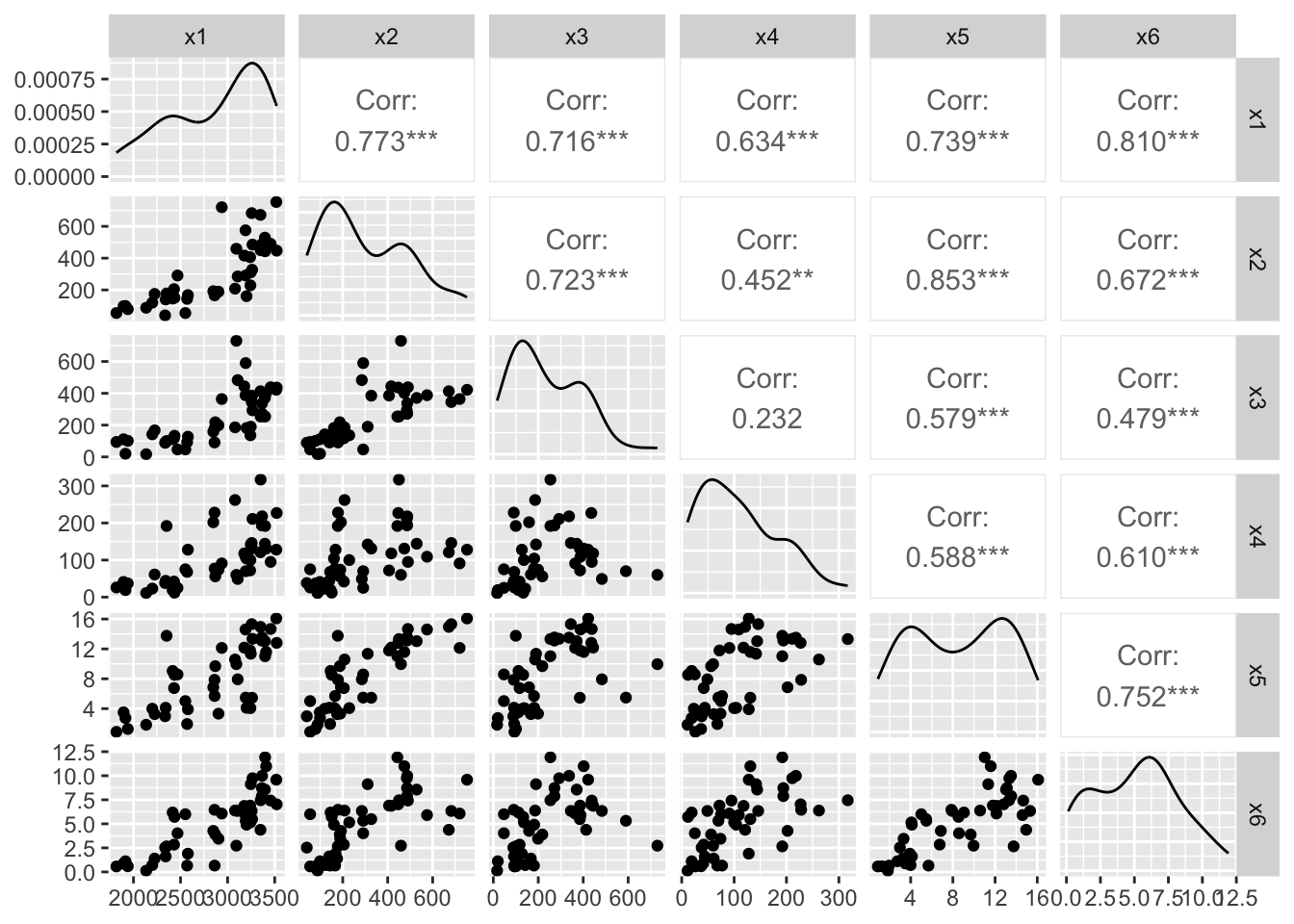
多重指標モデル
まずは多重指標モデルです。潜在変数としてxi1(洋食傾向)とeta1(下部消化管のガン傾向)を導入します。
semパッケージのモデル記述方法にはいくつかありますが、ここでは方程式によるものを使いました。「強制変換により NA が生成されました」という警告が大量にでるのですが、関係なさそうなので無視します。
model1_text <- "
x1 = 1 * xi1
x2 = lambda21 * xi1
x3 = lambda31 * xi1
x4 = lambda41 * xi1
x5 = 1 * eta1
x6 = kappa61 * eta1
eta1 = gamma11 * xi1
"
model1 <- specifyEquations(text = model1_text, covs = "xi1")
print(model1)
## Path Parameter StartValue
## 1 xi1 -> x1 <fixed> 1
## 2 xi1 -> x2 lambda21
## 3 xi1 -> x3 lambda31
## 4 xi1 -> x4 lambda41
## 5 eta1 -> x5 <fixed> 1
## 6 eta1 -> x6 kappa61
## 7 xi1 -> eta1 gamma11
## 8 xi1 <-> xi1 V[xi1]
## 9 x1 <-> x1 V[x1]
## 10 x2 <-> x2 V[x2]
## 11 x3 <-> x3 V[x3]
## 12 x4 <-> x4 V[x4]
## 13 eta1 <-> eta1 V[eta1]
## 14 x5 <-> x5 V[x5]
## 15 x6 <-> x6 V[x6]sem関数で当てはめを実行します。optimizer = optimizerOptimという引数をつけてオプティマイザをoptimizerOptimに指定していますが、これはデフォルトのoptimizerSemがいまひとつ不安定な気がするためです。とくに最後のPLSモデルでは、optimizerSemでは頻繁に収束に失敗しました。
結果が得られたら、要約を表示します。
fit1 <- sem(model1, S = cor(data), N = nrow(data),
optimizer = optimizerOptim)
summary(fit1)
##
## Model Chisquare = 46.91723 Df = 8 Pr(>Chisq) = 1.590119e-07
## AIC = 72.91723
## BIC = 16.11605
##
## Normalized Residuals
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -1.3286048 -0.3107604 -0.0000008 -0.0440850 0.3666662 0.5984950
##
## R-square for Endogenous Variables
## x1 x2 x3 x4 eta1 x5 x6
## 0.8164 0.7896 0.5192 0.3843 0.9614 0.8026 0.7053
##
## Parameter Estimates
## Estimate Std Error z value Pr(>|z|)
## lambda21 0.98347830 0.10898064 9.0243396 1.807825e-19 x2 <--- xi1
## lambda31 0.79745496 0.13194301 6.0439350 1.504001e-09 x3 <--- xi1
## lambda41 0.68612714 0.14233207 4.8206081 1.431213e-06 x4 <--- xi1
## kappa61 0.93738323 0.12049688 7.7793154 7.291807e-15 x6 <--- eta1
## gamma11 0.97225161 0.11181090 8.6954997 3.453066e-18 eta1 <--- xi1
## V[xi1] 0.81636717 0.20907763 3.9046126 9.437644e-05 xi1 <--> xi1
## V[x1] 0.18363262 0.05628028 3.2628231 1.103083e-03 x1 <--> x1
## V[x2] 0.21038587 0.05992048 3.5110845 4.462826e-04 x2 <--> x2
## V[x3] 0.48084431 0.10824544 4.4421668 8.905750e-06 x3 <--> x3
## V[x4] 0.61567831 0.13405388 4.5927674 4.374065e-06 x4 <--> x4
## V[eta1] 0.03095717 0.05846921 0.5294611 5.964856e-01 eta1 <--> eta1
## V[x5] 0.19735345 0.06694599 2.9479500 3.198888e-03 x5 <--> x5
## V[x6] 0.29472396 0.07700315 3.8274272 1.294896e-04 x6 <--> x6標準化係数を表示します。
stdCoef(fit1)
## Std. Estimate
## 1 0.90353049 x1 <--- xi1
## 2 lambda21 0.88860238 x2 <--- xi1
## 3 lambda31 0.72052469 x3 <--- xi1
## 4 lambda41 0.61993677 x4 <--- xi1
## 5 0.89590551 x5 <--- eta1
## 6 kappa61 0.83980712 x6 <--- eta1
## 7 gamma11 0.98052596 eta1 <--- xi1
## 8 V[xi1] 1.00000000 xi1 <--> xi1
## 9 V[x1] 0.18363265 x1 <--> x1
## 10 V[x2] 0.21038580 x2 <--> x2
## 11 V[x3] 0.48084417 x3 <--> x3
## 12 V[x4] 0.61567840 x4 <--> x4
## 13 V[eta1] 0.03856884 eta1 <--> eta1
## 14 V[x5] 0.19735332 x5 <--> x5
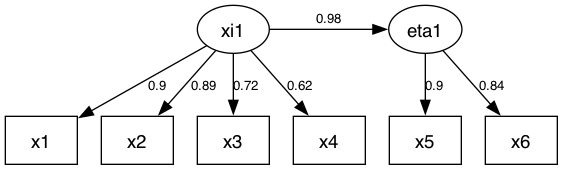
## 15 V[x6] 0.29472400 x6 <--> x6標準化係数を表示したパス図をファイルに出力します。
pathDiagram(fit1, standardize = TRUE,
file = "figures/model1",
output.type = "graphics",
graphics.fmt = "png",
edge.labels = "value",
rank.direction = "TB",
min.rank = c("eta1", "xi1"))
## Running dot -Tpng -o figures/model1.png -Gcharset=latin1 figures/model1.dot本の図表3-3aの結果と一致しました。
MIMIC model
つづいて、MIMICモデルです。潜在変数のeta1は下部消化管のガン傾向をあらわします。
model2_text <- "
eta1 = gamma11 * x1 + gamma12 * x2 + gamma13 * x3 + gamma14 * x4
x5 = 1 * eta1
x6 = kappa61 * eta1
"
model2 <- specifyEquations(text = model2_text, covs = "x1, x2, x3, x4")
print(model2)
## Path Parameter StartValue
## 1 x1 -> eta1 gamma11
## 2 x2 -> eta1 gamma12
## 3 x3 -> eta1 gamma13
## 4 x4 -> eta1 gamma14
## 5 eta1 -> x5 <fixed> 1
## 6 eta1 -> x6 kappa61
## 7 x1 <-> x1 V[x1]
## 8 x1 <-> x2 C[x1,x2]
## 9 x1 <-> x3 C[x1,x3]
## 10 x1 <-> x4 C[x1,x4]
## 11 x2 <-> x2 V[x2]
## 12 x2 <-> x3 C[x2,x3]
## 13 x2 <-> x4 C[x2,x4]
## 14 x3 <-> x3 V[x3]
## 15 x3 <-> x4 C[x3,x4]
## 16 x4 <-> x4 V[x4]
## 17 eta1 <-> eta1 V[eta1]
## 18 x5 <-> x5 V[x5]
## 19 x6 <-> x6 V[x6]あてはめを実行して、結果の要約を表示します。
fit2 <- sem(model2, S = cor(data), N = nrow(data),
optimizer = optimizerOptim)
summary(fit2)
##
## Model Chisquare = 17.34207 Df = 3 Pr(>Chisq) = 0.0006010001
## AIC = 53.34207
## BIC = 5.791629
##
## Normalized Residuals
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -0.3885292 -0.0000008 0.0000000 0.0068182 0.0000016 0.5215193
##
## R-square for Endogenous Variables
## eta1 x5 x6
## 0.9225 0.8271 0.6844
##
## Parameter Estimates
## Estimate Std Error z value Pr(>|z|)
## gamma11 0.30127640 0.13426497 2.243894 2.483920e-02 eta1 <--- x1
## gamma12 0.58835075 0.11056030 5.321537 1.028941e-07 eta1 <--- x2
## gamma13 -0.12151973 0.10741969 -1.131261 2.579452e-01 eta1 <--- x3
## gamma14 0.18516888 0.09014142 2.054204 3.995594e-02 eta1 <--- x4
## kappa61 0.90964924 0.11431238 7.957574 1.754451e-15 x6 <--- eta1
## V[x1] 1.00000000 0.20851441 4.795832 1.620014e-06 x1 <--> x1
## C[x1,x2] 0.77311094 0.18636690 4.148328 3.349129e-05 x2 <--> x1
## C[x1,x3] 0.71552497 0.18129822 3.946674 7.924431e-05 x3 <--> x1
## C[x1,x4] 0.63412405 0.17458730 3.632132 2.810896e-04 x4 <--> x1
## V[x2] 1.00000000 0.20851441 4.795832 1.620014e-06 x2 <--> x2
## C[x2,x3] 0.72279966 0.18192446 3.973076 7.095045e-05 x3 <--> x2
## C[x2,x4] 0.45159335 0.16177927 2.791417 5.247789e-03 x4 <--> x2
## V[x3] 1.00000000 0.20851441 4.795832 1.620014e-06 x3 <--> x3
## C[x3,x4] 0.23213341 0.15136236 1.533627 1.251214e-01 x4 <--> x3
## V[x4] 1.00000000 0.20851441 4.795832 1.620014e-06 x4 <--> x4
## V[eta1] 0.06410761 0.04949196 1.295314 1.952121e-01 eta1 <--> eta1
## V[x5] 0.17288215 0.05975163 2.893346 3.811607e-03 x5 <--> x5
## V[x6] 0.31559003 0.07671432 4.113835 3.891398e-05 x6 <--> x6標準化係数を表示します。
stdCoef(fit2)
## Std. Estimate
## gamma11 gamma11 0.33126933 eta1 <--- x1
## gamma12 gamma12 0.64692277 eta1 <--- x2
## gamma13 gamma13 -0.13361737 eta1 <--- x3
## gamma14 gamma14 0.20360297 eta1 <--- x4
## 0.90946026 x5 <--- eta1
## kappa61 kappa61 0.82729055 x6 <--- eta1
## V[x1] V[x1] 1.00000000 x1 <--> x1
## C[x1,x2] C[x1,x2] 0.77311094 x2 <--> x1
## C[x1,x3] C[x1,x3] 0.71552497 x3 <--> x1
## C[x1,x4] C[x1,x4] 0.63412405 x4 <--> x1
## V[x2] V[x2] 1.00000000 x2 <--> x2
## C[x2,x3] C[x2,x3] 0.72279966 x3 <--> x2
## C[x2,x4] C[x2,x4] 0.45159335 x4 <--> x2
## V[x3] V[x3] 1.00000000 x3 <--> x3
## C[x3,x4] C[x3,x4] 0.23213341 x4 <--> x3
## V[x4] V[x4] 1.00000000 x4 <--> x4
## V[eta1] V[eta1] 0.07750716 eta1 <--> eta1
## V[x5] V[x5] 0.17288203 x5 <--> x5
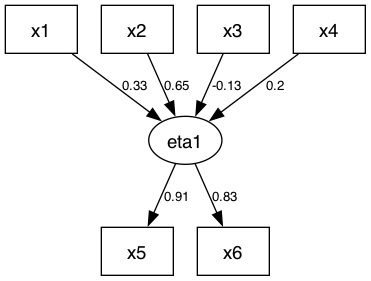
## V[x6] V[x6] 0.31559035 x6 <--> x6パス図を出力します。
pathDiagram(fit2, standardize = TRUE,
file = "figures/model2",
output.type = "graphics",
graphics.fmt = "png",
edge.labels = "value",
rank.direction = "TB")
## Running dot -Tpng -o figures/model2.png -Gcharset=latin1 figures/model2.dot本の図表3-3bと同じ結果が得られました。
PLS model
最後にPLSモデルです。多重指標モデルと同じく、潜在変数はxi1(洋食傾向)とeta1(下部消化管のガン傾向)です。
model3_text <- "
xi1 = gamma11 * x1 + gamma12 * x2 + gamma13 * x3 + gamma14 * x4
x5 = 1 * eta1
x6 = kappa61 * eta1
eta1 = 1 * xi1
V(xi1) = 0
"
model3 <- specifyEquations(text = model3_text, covs = "x1, x2, x3, x4")
print(model3)
## Path Parameter StartValue
## 1 x1 -> xi1 gamma11
## 2 x2 -> xi1 gamma12
## 3 x3 -> xi1 gamma13
## 4 x4 -> xi1 gamma14
## 5 eta1 -> x5 <fixed> 1
## 6 eta1 -> x6 kappa61
## 7 xi1 -> eta1 <fixed> 1
## 8 xi1 <-> xi1 <fixed> 0
## 9 x1 <-> x1 V[x1]
## 10 x1 <-> x2 C[x1,x2]
## 11 x1 <-> x3 C[x1,x3]
## 12 x1 <-> x4 C[x1,x4]
## 13 x2 <-> x2 V[x2]
## 14 x2 <-> x3 C[x2,x3]
## 15 x2 <-> x4 C[x2,x4]
## 16 x3 <-> x3 V[x3]
## 17 x3 <-> x4 C[x3,x4]
## 18 x4 <-> x4 V[x4]
## 19 eta1 <-> eta1 V[eta1]
## 20 x5 <-> x5 V[x5]
## 21 x6 <-> x6 V[x6]あてはめます。
fit3 <- sem(model3, S = cor(data), N = nrow(data),
optimizer = optimizerOptim)
summary(fit3)
##
## Model Chisquare = 17.34207 Df = 3 Pr(>Chisq) = 0.0006010001
## AIC = 53.34207
## BIC = 5.791629
##
## Normalized Residuals
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -0.3885310 -0.0000005 0.0000000 0.0068179 0.0000005 0.5215156
##
## R-square for Endogenous Variables
## xi1 eta1 x5 x6
## 1.0000 0.9225 0.8271 0.6844
##
## Parameter Estimates
## Estimate Std Error z value Pr(>|z|)
## gamma11 0.30127779 0.13426491 2.243906 2.483847e-02 xi1 <--- x1
## gamma12 0.58835028 0.11056025 5.321535 1.028952e-07 xi1 <--- x2
## gamma13 -0.12152055 0.10741964 -1.131269 2.579417e-01 xi1 <--- x3
## gamma14 0.18516821 0.09014137 2.054198 3.995655e-02 xi1 <--- x4
## kappa61 0.90965003 0.11431246 7.957575 1.754433e-15 x6 <--- eta1
## V[x1] 1.00000000 0.20851441 4.795832 1.620014e-06 x1 <--> x1
## C[x1,x2] 0.77311094 0.18636690 4.148328 3.349129e-05 x2 <--> x1
## C[x1,x3] 0.71552497 0.18129822 3.946674 7.924431e-05 x3 <--> x1
## C[x1,x4] 0.63412405 0.17458730 3.632132 2.810896e-04 x4 <--> x1
## V[x2] 1.00000000 0.20851441 4.795832 1.620014e-06 x2 <--> x2
## C[x2,x3] 0.72279966 0.18192446 3.973076 7.095045e-05 x3 <--> x2
## C[x2,x4] 0.45159335 0.16177927 2.791417 5.247789e-03 x4 <--> x2
## V[x3] 1.00000000 0.20851441 4.795832 1.620014e-06 x3 <--> x3
## C[x3,x4] 0.23213340 0.15136236 1.533627 1.251214e-01 x4 <--> x3
## V[x4] 1.00000000 0.20851441 4.795832 1.620014e-06 x4 <--> x4
## V[eta1] 0.06410734 0.04949190 1.295310 1.952134e-01 eta1 <--> eta1
## V[x5] 0.17288245 0.05975162 2.893352 3.811545e-03 x5 <--> x5
## V[x6] 0.31558997 0.07671432 4.113834 3.891414e-05 x6 <--> x6標準化係数を表示します。
stdCoef(fit3)
## Std. Estimate
## 1 gamma11 0.34490686 xi1 <--- x1
## 2 gamma12 0.67355130 xi1 <--- x2
## 3 gamma13 -0.13911836 xi1 <--- x3
## 4 gamma14 0.21198306 xi1 <--- x4
## 5 0.90946007 x5 <--- eta1
## 6 kappa61 0.82729070 x6 <--- eta1
## 7 0.96046505 eta1 <--- xi1
## 8 0.00000000 xi1 <--> xi1
## 9 V[x1] 1.00000000 x1 <--> x1
## 10 C[x1,x2] 0.77311095 x2 <--> x1
## 11 C[x1,x3] 0.71552497 x3 <--> x1
## 12 C[x1,x4] 0.63412405 x4 <--> x1
## 13 V[x2] 1.00000000 x2 <--> x2
## 14 C[x2,x3] 0.72279966 x3 <--> x2
## 15 C[x2,x4] 0.45159335 x4 <--> x2
## 16 V[x3] 1.00000000 x3 <--> x3
## 17 C[x3,x4] 0.23213340 x4 <--> x3
## 18 V[x4] 1.00000000 x4 <--> x4
## 19 V[eta1] 0.07750689 eta1 <--> eta1
## 20 V[x5] 0.17288239 x5 <--> x5
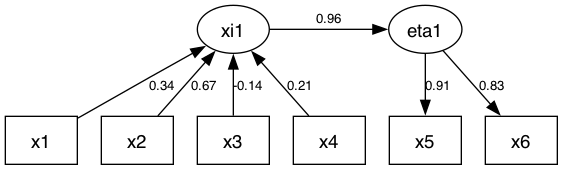
## 21 V[x6] 0.31559010 x6 <--> x6パス図を出力します。
pathDiagram(fit3, standardize = TRUE,
file = "figures/model3",
output.type = "graphics",
graphics.fmt = "png",
edge.labels = "value",
rank.direction = "TB",
min.rank = c("eta1", "xi1"))
## Running dot -Tpng -o figures/model3.png -Gcharset=latin1 figures/model3.dot本の図表3-3cと同じ結果が得られました。
おわりに
ここまでsemパッケージをつかっておいてなんですが、なんだかlavaanパッケージの方が使いやすい気がしました。