『ポアソン分布・ポアソン回帰・ポアソン過程』第1章の図をRで再現する

『ポアソン分布・ポアソン回帰・ポアソン過程』（島谷健一郎著, 近代科学社, 2017）の第1章「ポアソン分布の2つの起源」から、ランダムなイベントとポアソン分布との関係をしめす図2つと、ポアソン乱数の生成の図1つをRで再現してみました。

準備

作図のためggplot2パッケージを読み込みます。また、擬似乱数を固定します。フォントも設定します。

library(ggplot2)

set.seed(123)
jp_font <- "YuGothic"

図 1.5 大きな点配置のごく一部のイベント発生回数

長さ10000のなかに40000個の点をランダムに配置し、そのなかで0から1の長さ1の部分に入っている点の数を求めるというシミュレーションをおこないます。シミュレーションは10000回くりかえし、入った点の個数の割合を求めます。

まず、シミュレーション用の関数を定義します。長さlengthと、点の数nを引数として、0〜1の間に入った点の個数を返します。

sim_dpois1 <- function(length = 10000, n = length * 4) {
  p <- runif(n, 0, length)
  sum(p < 1)
}

R=10000回繰り返して、点の個数の分布割合とポアソン分布の確率とを比較します。

R <- 10000
y <- replicate(R, sim_dpois1(10000, 40000))
x <- 0:max(y)
n <- factor(y, levels = x) |>
  table()
n_pois <- dpois(x, 4)

legend_label <- c("シミュレーション", "ポアソン分布")
data.frame(x = rep(x, 2),
           prop = c(n / R, n_pois),
           item = rep(factor(legend_label),
                             levels = legend_label,
                      each = length(x))) |>
  ggplot(aes(x = x, y = prop, fill = item)) +
  geom_col(position = "dodge") +
  labs(x = "長さ1の部分に入った個数", y = "割合") +
  scale_fill_discrete(name = "") +
  theme_gray(base_family = jp_font)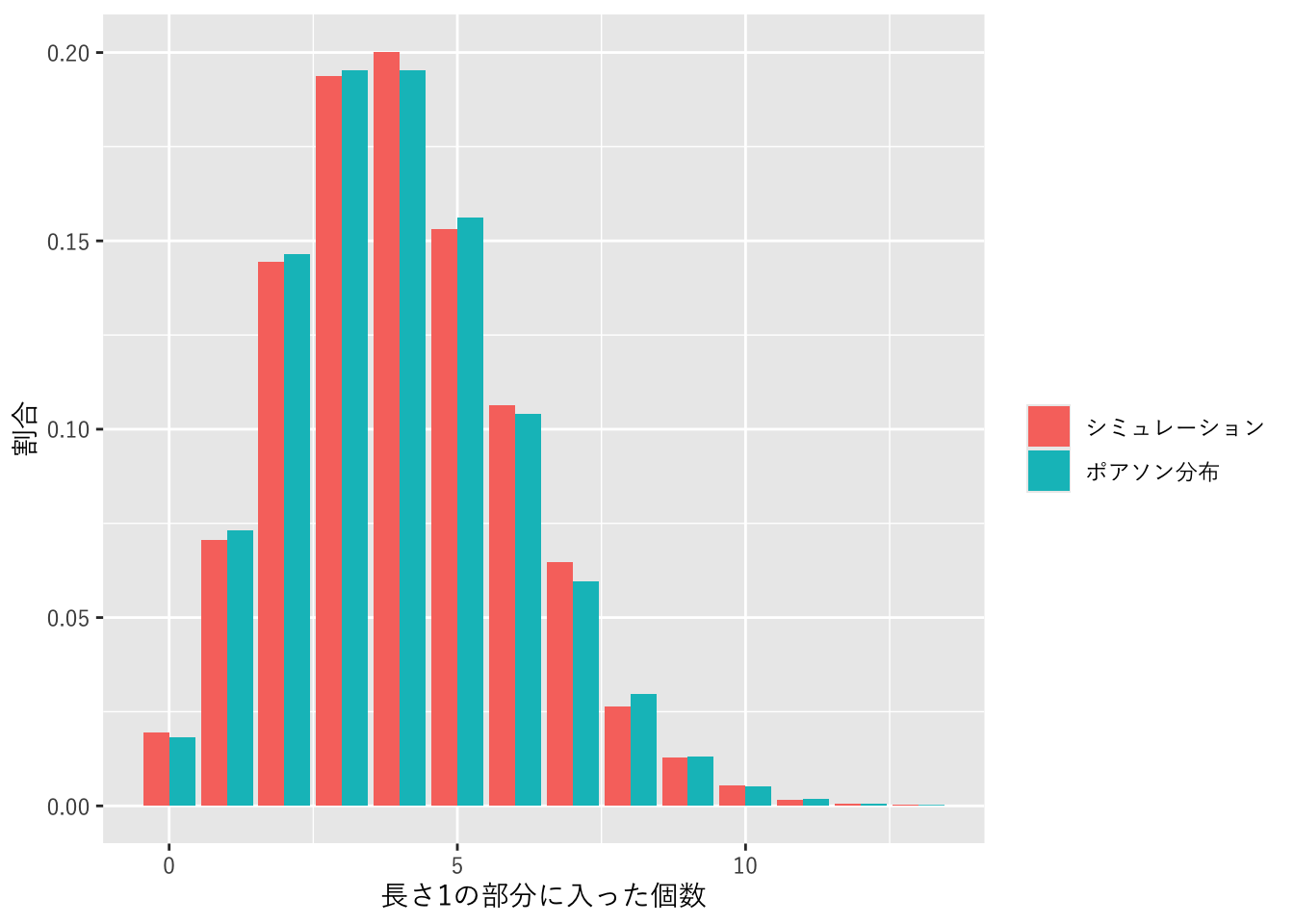

だいたいポアソン分布の確率どおりの結果となりました。

図 1.7 時間を細かく分割したときのイベント発生回数

長さ1の区間を10000等分し（等分された区間の長さはh=0.0001）、それぞれの区間で独立にrh=0.0004の確率でイベントが発生するとします。全区間でのイベントの発生回数を集計して、その値を求めるというシミュレーションをおこないます。シミュレーションは10000回くりかえし、イベントの発生回数合計値の割合を求めます。

まず、シミュレーション用の関数を定義します。区間の長さhと、イベントの発生確率rhを引数として、全区間でのイベントの発生回数を返します。

sim_dpois2 <- function(h = 0.0001, rh = h * 4) {
  rbinom(1 / h, 1, rh) |>
    sum()
}

R=10000回繰り返して、発生回数の分布割合とポアソン分布の確率とを比較します。

R <- 10000
y <- replicate(R, sim_dpois2(0.0001, 0.0004))
x <- 0:max(y)
n <- factor(y, levels = x) |>
  table()
n_pois <- dpois(x, 4)

data.frame(x = rep(x, 2),
           prop = c(n / R, n_pois),
           item = rep(factor(legend_label),
                             levels = legend_label,
                      each = length(x))) |>
  ggplot(aes(x = x, y = prop, fill = item)) +
  geom_col(position = "dodge") +
  labs(x = "全体での総数", y = "割合") +
  scale_fill_discrete(name = "") +
  theme_gray(base_family = jp_font)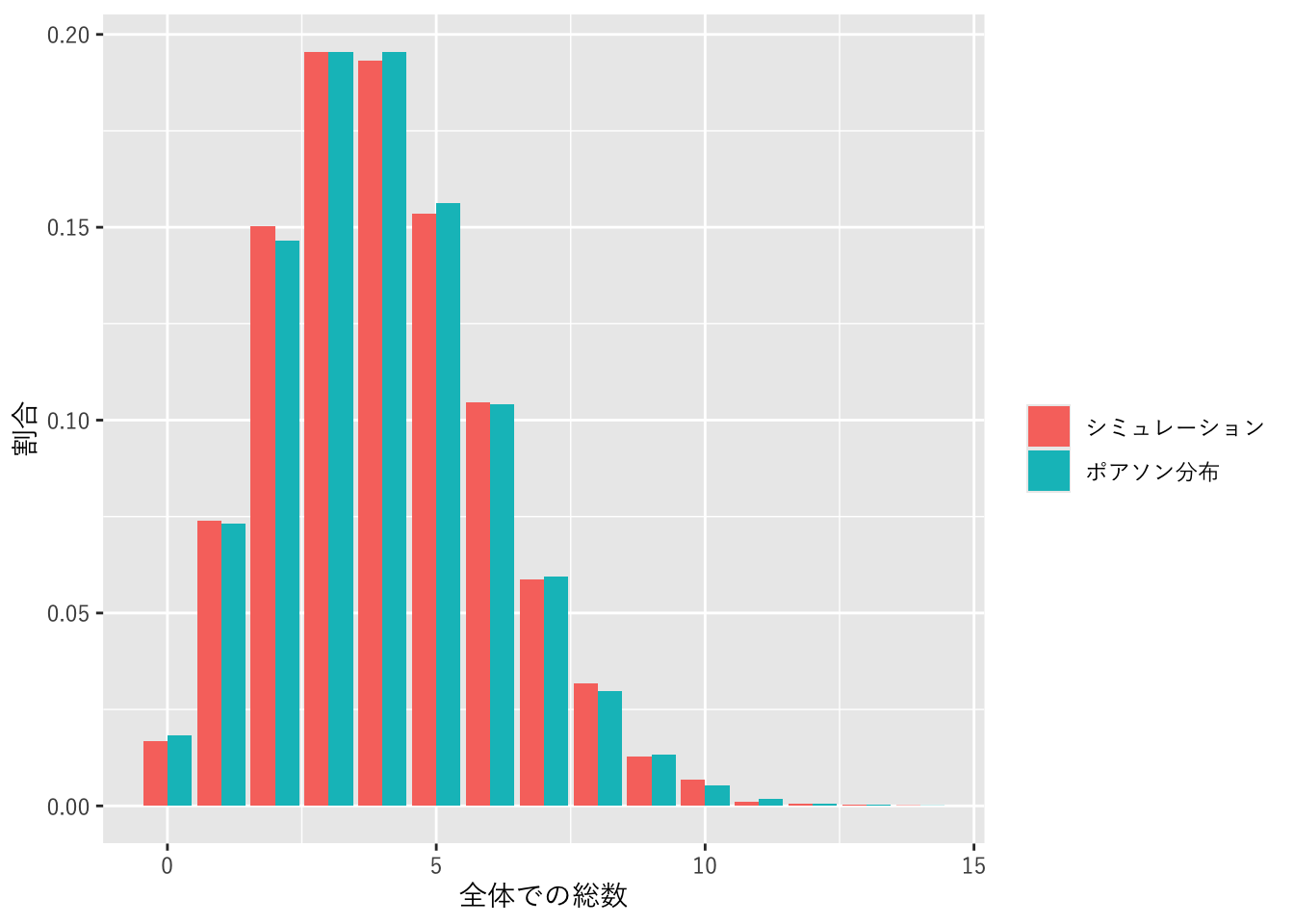

だいたいポアソン分布の確率どおりの結果となりました。

図 1.8 ポアソン分布にしたがう乱数

ポアソン分布にしたがう乱数を発生させます。

0〜1の一様乱数を生成して、それがポアソン分布の累積確率のどこに入っているのかを返す関数を定義します。nは発生させる乱数の個数、lambdaは強度、max_xは返す乱数の最大値です。

sim_rpois <- function(n = 100, lambda = 4, max_x = 20) {
  cum_prob <- sapply(0:max_x,
                     function(k)
                       lambda^k * exp(-lambda) / factorial(k)) |>
    cumsum()
  p <- runif(n, 0, 1)
  sapply(1:n, function(i) sum(p[i] > cum_prob))
}

1000個の乱数を発生させて、ポアソン分布から計算される期待値と比較します。

R <- 10000
y <- sim_rpois(n = R, lambda = 4, max_x = 20)
x <- 0:max(y)
n <- factor(y, levels = x) |>
  table()
n_pois <- R * dpois(x, 4)

data.frame(x = rep(x, 2),
           n = c(n, n_pois),
           item = rep(factor(c("生成された乱数", "期待値"),
                             levels = c("生成された乱数", "期待値")),
                      each = length(x))) |>
  ggplot(aes(x = x, y = n, fill = item)) +
  geom_col(position = "dodge") +
  labs(x = "値", y = "個数") +
  scale_fill_discrete(name = "") +
  theme_gray(base_family = jp_font)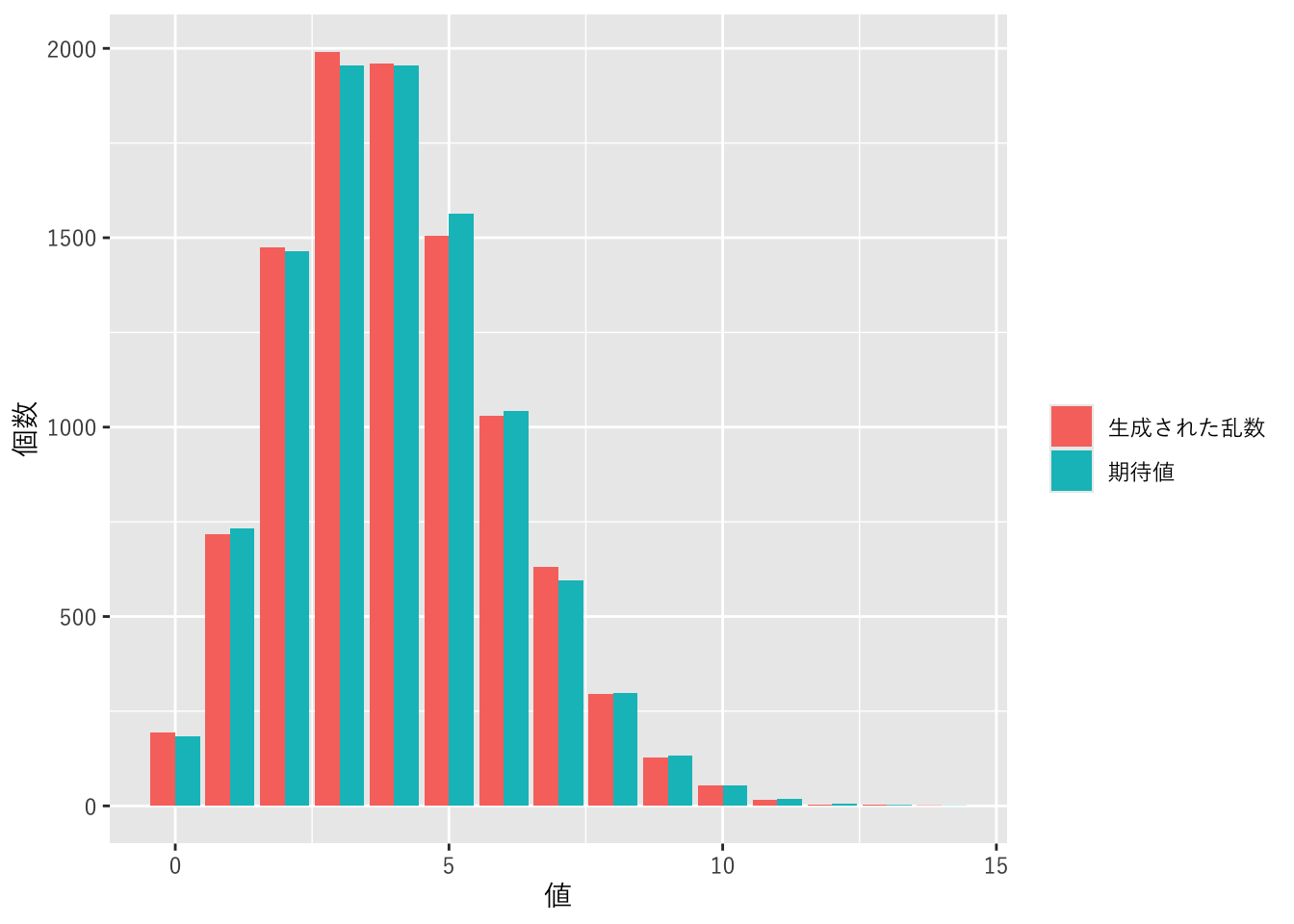

ほぼ期待値どおりの割合で生成されました。

おわりに

ここでは図を3つ再現しただけですが、本文を読むとポアソン分布の理解がすすみます。