library(ggplot2)
set.seed(123)『ポアソン分布・ポアソン回帰・ポアソン過程』(島谷健一郎著, 近代科学社, 2017)の第5章「空間点過程モデルの第1歩:非定常ポアソン過程」にある、非定常ポアソン過程による点配置やモデルあてはめをRでやってみました。今回は本の元データがないので、だいだい相当するようなことをやっています。ついでにL関数もためしています。
準備
作図のためggplot2パッケージを読み込みます。
また、擬似乱数を固定します。
場所によって密度の異なる点配置
図 5.1の、正方形を4分割して、小正方形ごとに平均密度が異なるという点配置をやってみます。
まず、指定した強度の定常ポアソン過程で点を配置する関数を定義します。
ppois2d <- function(lambda, x_range, y_range) {
n <- rpois(1, lambda)
x <- runif(n, x_range[1], x_range[2])
y <- runif(n, y_range[1], y_range[2])
data.frame(x = x, y = y)
}平均密度が異なる小方形区に強度を変えて点を配置し、それらをまとめ、最後に図示します。
p <- list()
p[[1]] <- ppois2d(2 * 4, c(0, 50), c(0, 50))
p[[2]] <- ppois2d(4 * 4, c(0, 50), c(50, 100))
p[[3]] <- ppois2d(6 * 4, c(50, 100), c(50, 100))
p[[4]] <- ppois2d(8 * 4, c(50, 100), c(0, 50))
pp <- dplyr::bind_rows(p)
ggplot(pp, aes(x = x, y = y)) +
geom_point() +
scale_x_continuous(limits = c(0, 100)) +
scale_y_continuous(limits = c(0, 100)) +
coord_fixed()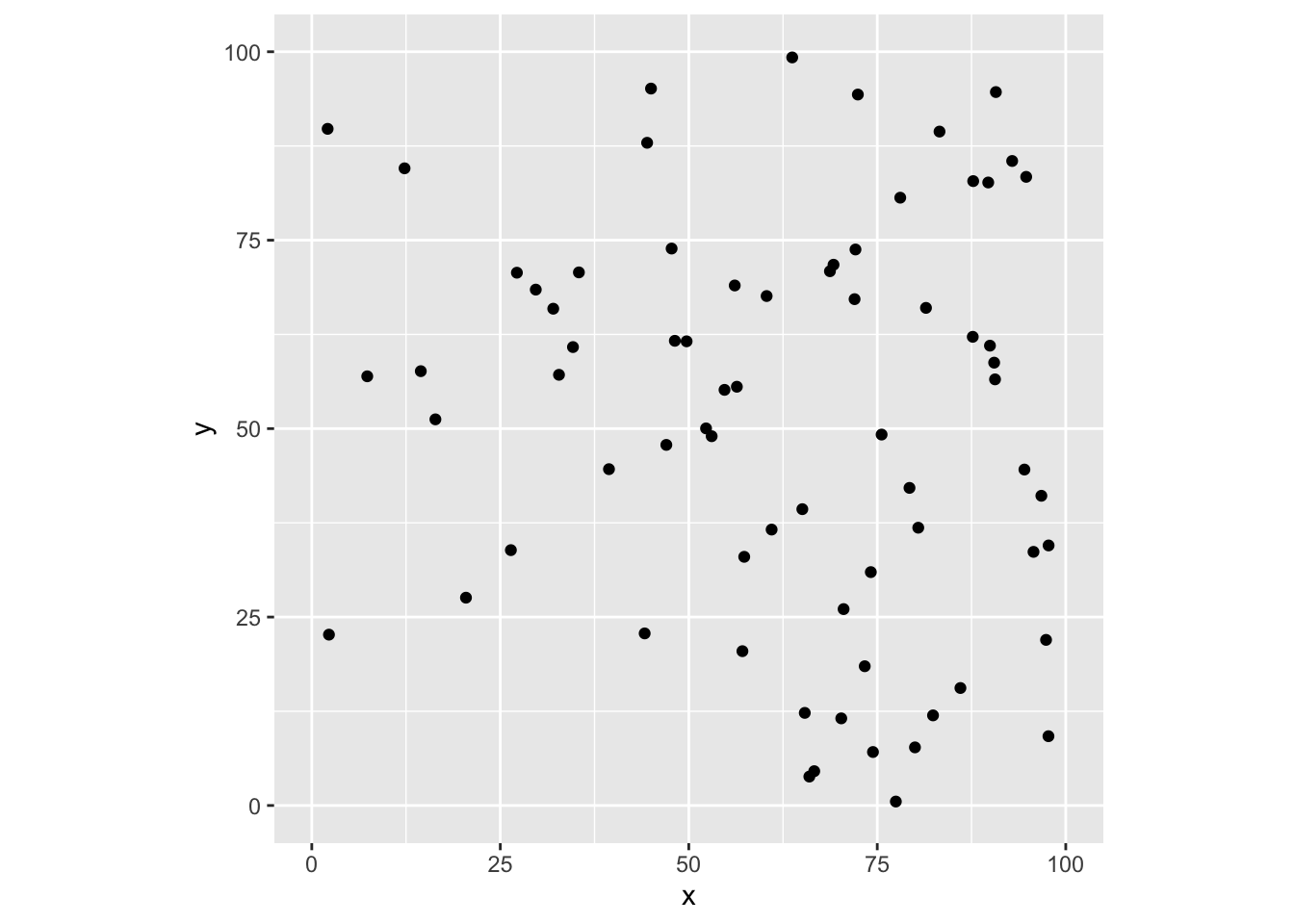
次に、座標により強度が変わる点配置です。
まず、強度rが r(x, y) = 0.001xという値をとる配置です(図 5.2(a))。
p <- expand.grid(x = 0:99, y = 0:99)
n <- nrow(p)
z <- rbinom(n, size = 1,
prob = 0.001 * (p$x + 0.5))
x <- z * runif(n, p$x, p$x + 1)
y <- z * runif(n, p$y, p$y + 1)
x <- x[x > 0]
y <- y[y > 0]
ggplot(data.frame(x = x, y = y),
aes(x = x, y = y)) +
geom_point() +
scale_x_continuous(limits = c(0, 100)) +
scale_y_continuous(limits = c(0, 100)) +
coord_fixed()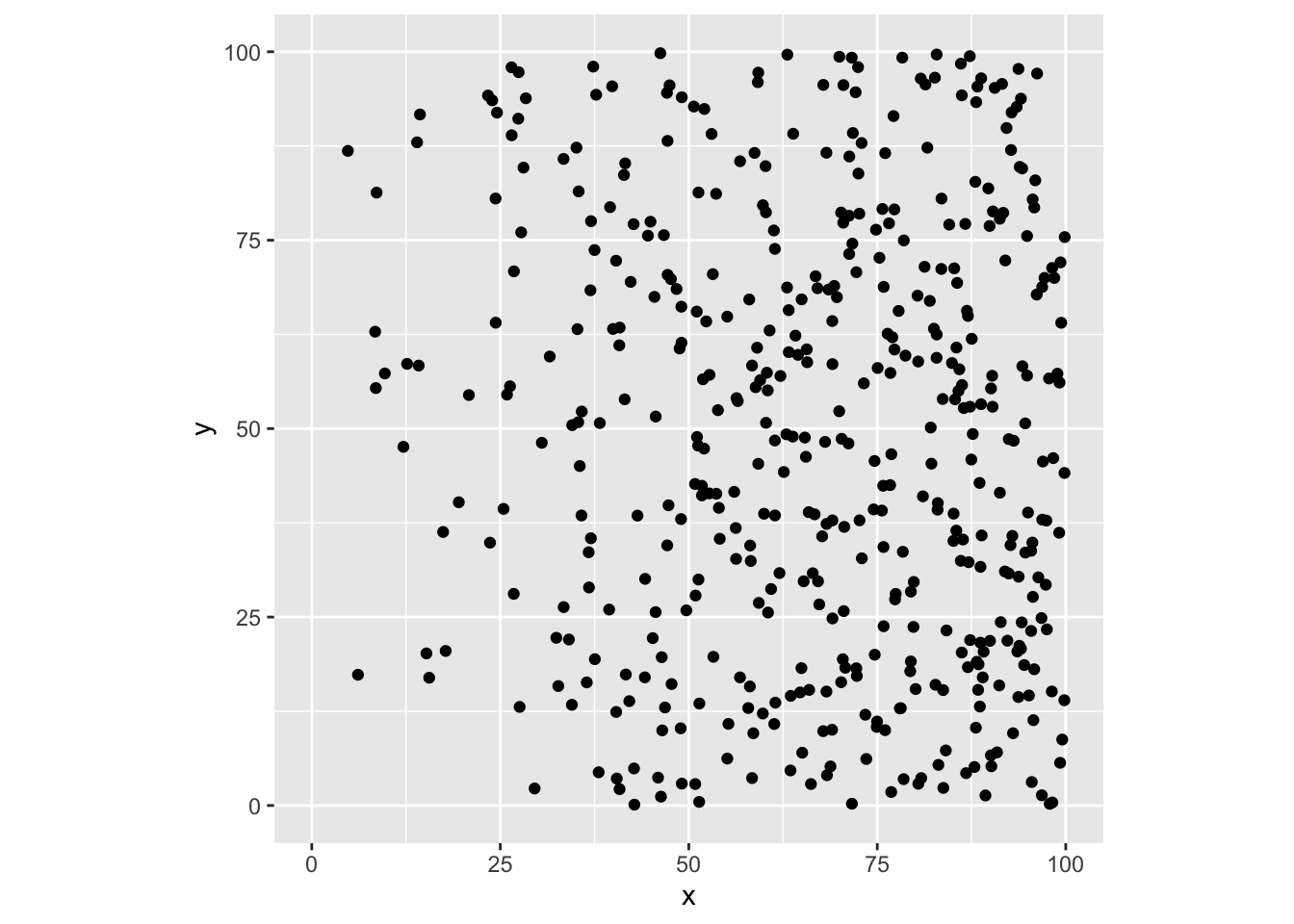
つづいて、強度rが r(x, y) = (-0.00002 (x - 40)2 + 0.05) × 0.04 yという値をとる配置です(図 5.2(b))。
p <- expand.grid(x = seq(0.5, 99.5, 1),
y = seq(0.5, 99.5, 1))
n <- nrow(p)
r <- (-0.00002 * (p$x - 40)^2 + 0.05) * 0.04 * p$y
r[r < 0] <- 0
z <- rbinom(n, size = 1, prob = r)
x <- z * runif(n, p$x - 0.5, p$x + 0.5)
y <- z * runif(n, p$y - 0.5, p$y + 0.5)
ggplot(data.frame(x = x, y = y),
aes(x = x, y = y)) +
geom_point() +
scale_x_continuous(limits = c(0, 100)) +
scale_y_continuous(limits = c(0, 100)) +
coord_fixed()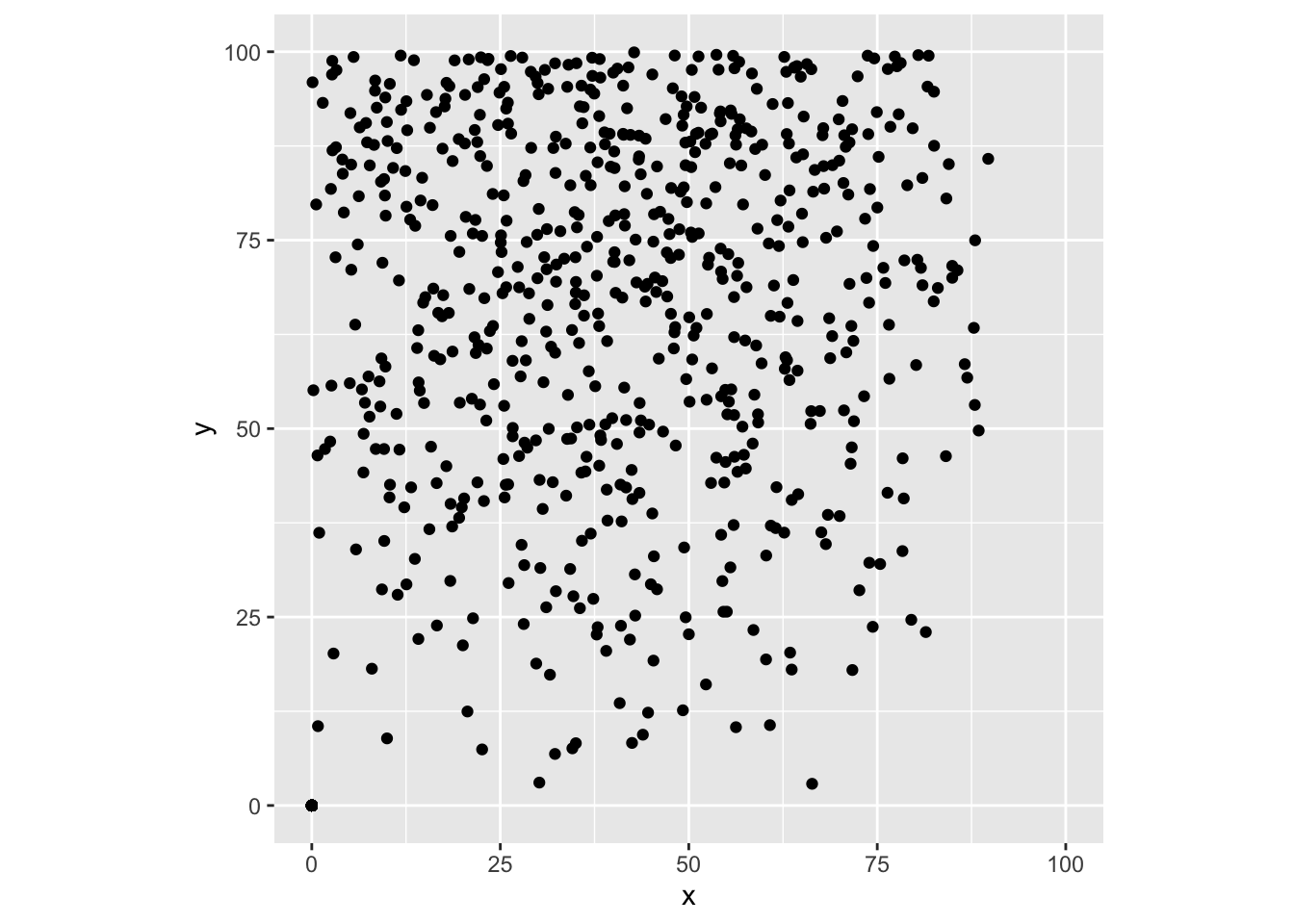
spatstatパッケージ
Rではspatstatパッケージで点パターンを扱うことができます。
強度0.01の定常ポアソン過程による点パターンを作成します。
library(spatstat)
## 要求されたパッケージ spatstat.data をロード中です
## 要求されたパッケージ spatstat.univar をロード中です
## spatstat.univar 3.1-2
## 要求されたパッケージ spatstat.geom をロード中です
## spatstat.geom 3.3-6
## 要求されたパッケージ spatstat.random をロード中です
## spatstat.random 3.3-3
## 要求されたパッケージ spatstat.explore をロード中です
## 要求されたパッケージ nlme をロード中です
## spatstat.explore 3.3-4
## 要求されたパッケージ spatstat.model をロード中です
## 要求されたパッケージ rpart をロード中です
## spatstat.model 3.3-4
## 要求されたパッケージ spatstat.linnet をロード中です
## spatstat.linnet 3.2-5
##
## spatstat 3.3-1
## For an introduction to spatstat, type 'beginner'
pp1 <- rpoispp(lambda = 0.01,
win = owin(xrange = c(0, 100), yrange = c(0, 100)))配置された点の数です。期待値は100ですが、乱数によるばらつきがあります。
pp1$n
## [1] 84図示します。
plot(pp1)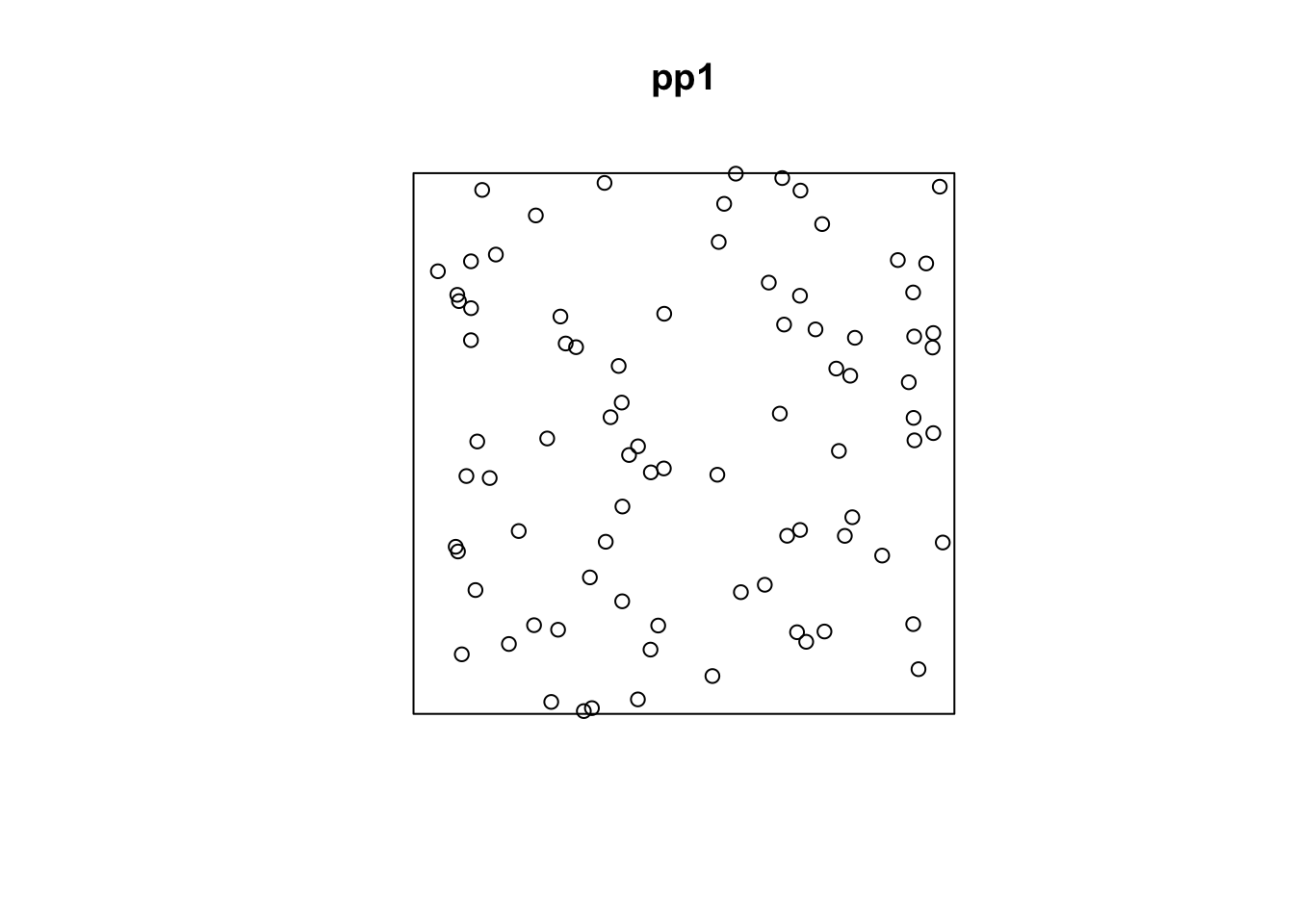
ggplot2でも作図してみようということで、pppクラスの点パターンをsfクラスに変換して、geom_sf関数で図示します。
sf::st_as_sf(pp1) |>
ggplot() +
geom_sf(fill = NA)
カーネル平滑化
点パターンからカーネル平滑化強度を求め、それに点を重ねて図示します(図 5.5に相当)。
dens1 <- density(pp1)
plot(dens1)
points(pp1)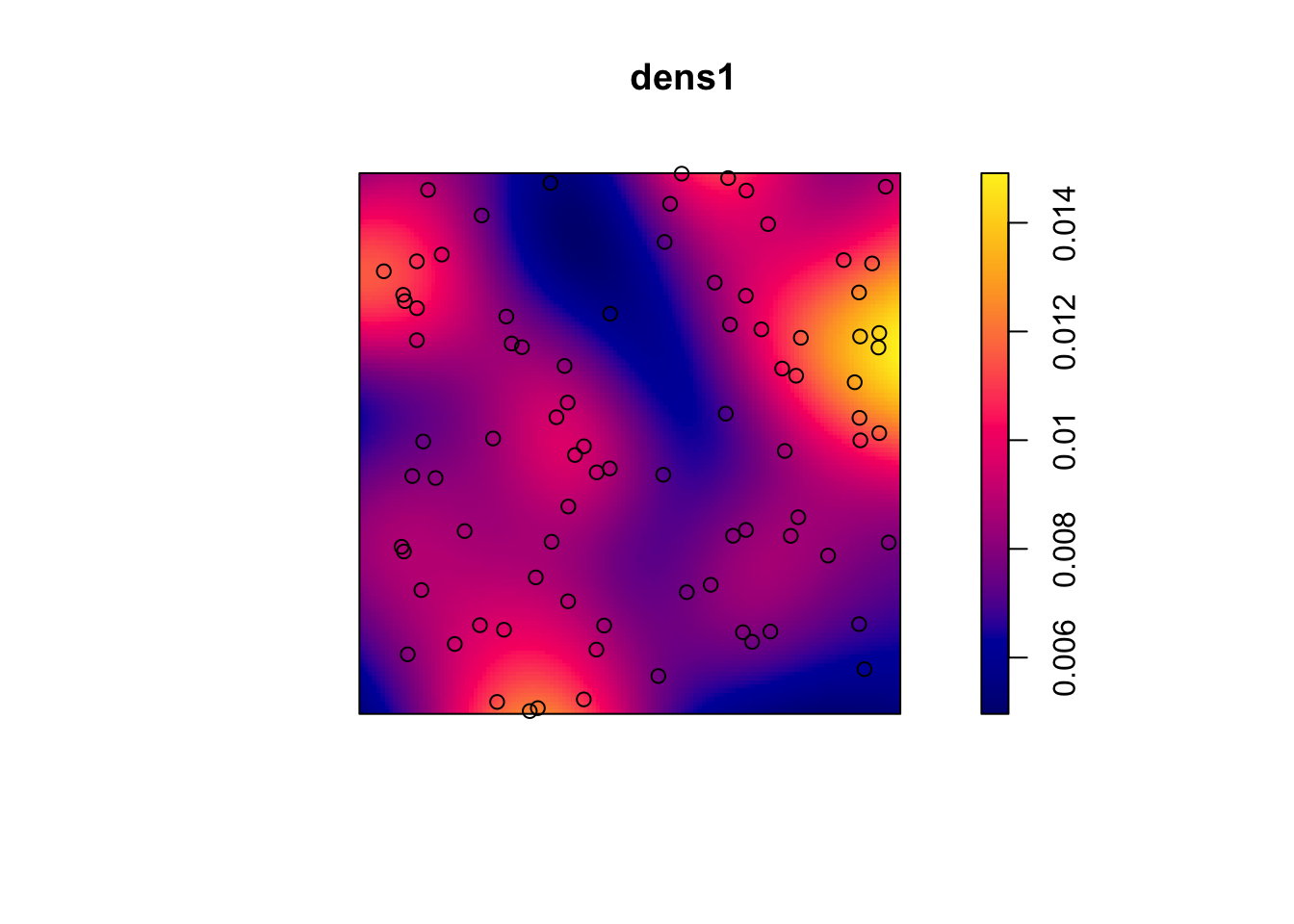
ggplot2でもやってみます。
expand.grid(y = dens1$yrow, x = dens1$xcol) |>
cbind(Intensity = c(dens1$v)) |>
ggplot() +
geom_tile(aes(x = x, y = y, fill = Intensity)) +
scale_fill_continuous(type = "viridis") +
geom_point(data = data.frame(x = pp1$x, y = pp1$y),
mapping = aes(x = x, y = y)) +
coord_fixed()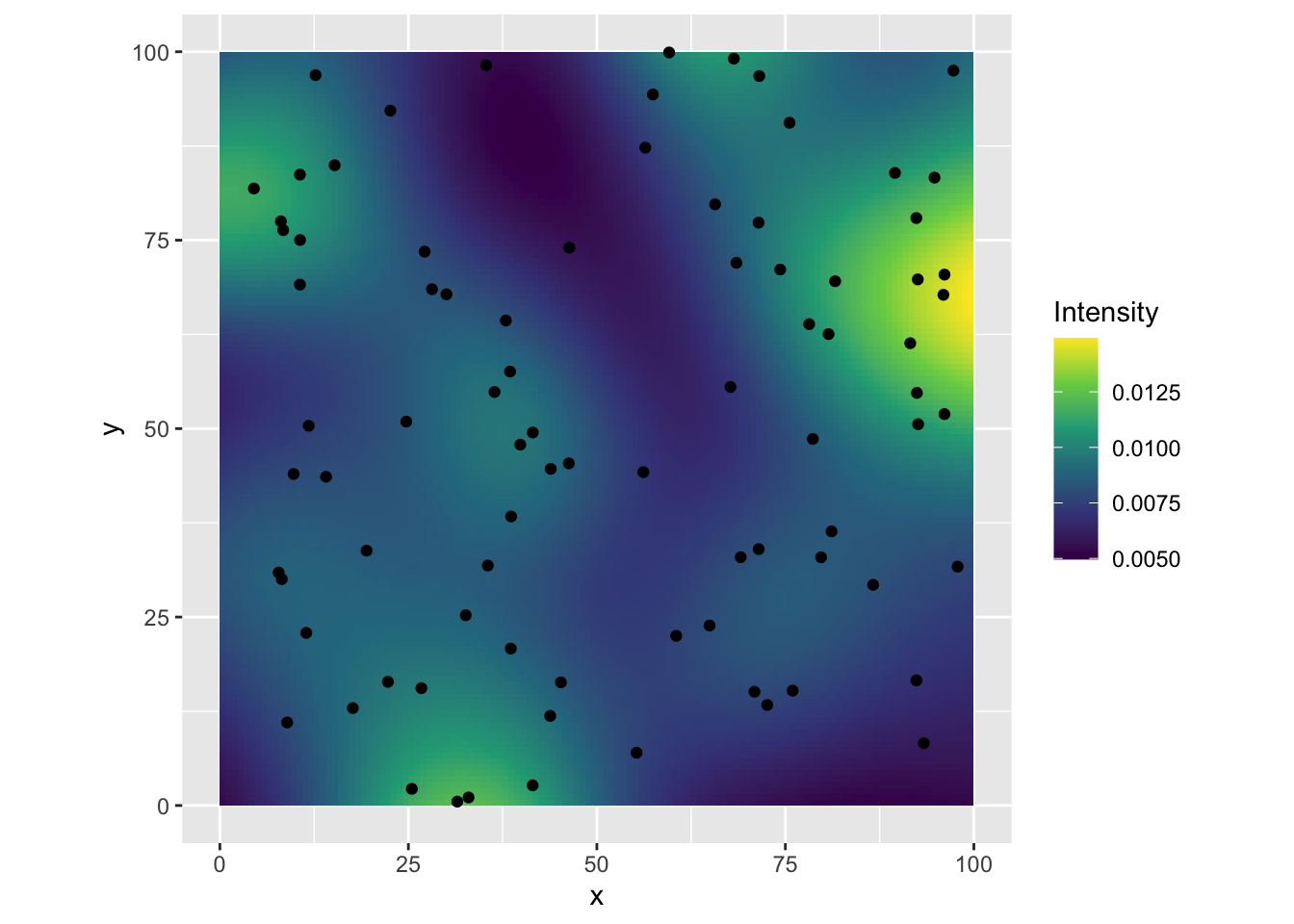
非定常ポアソン過程
非定常ポアソン過程により点を配置します。
まず図 5.3(a)です。
W <- owin(xrange = c(0, 100), yrange = c(0, 100))
pp2 <- rpoispp(lambda = function(x, y) {0.001 * x},
win = W)
plot(pp2)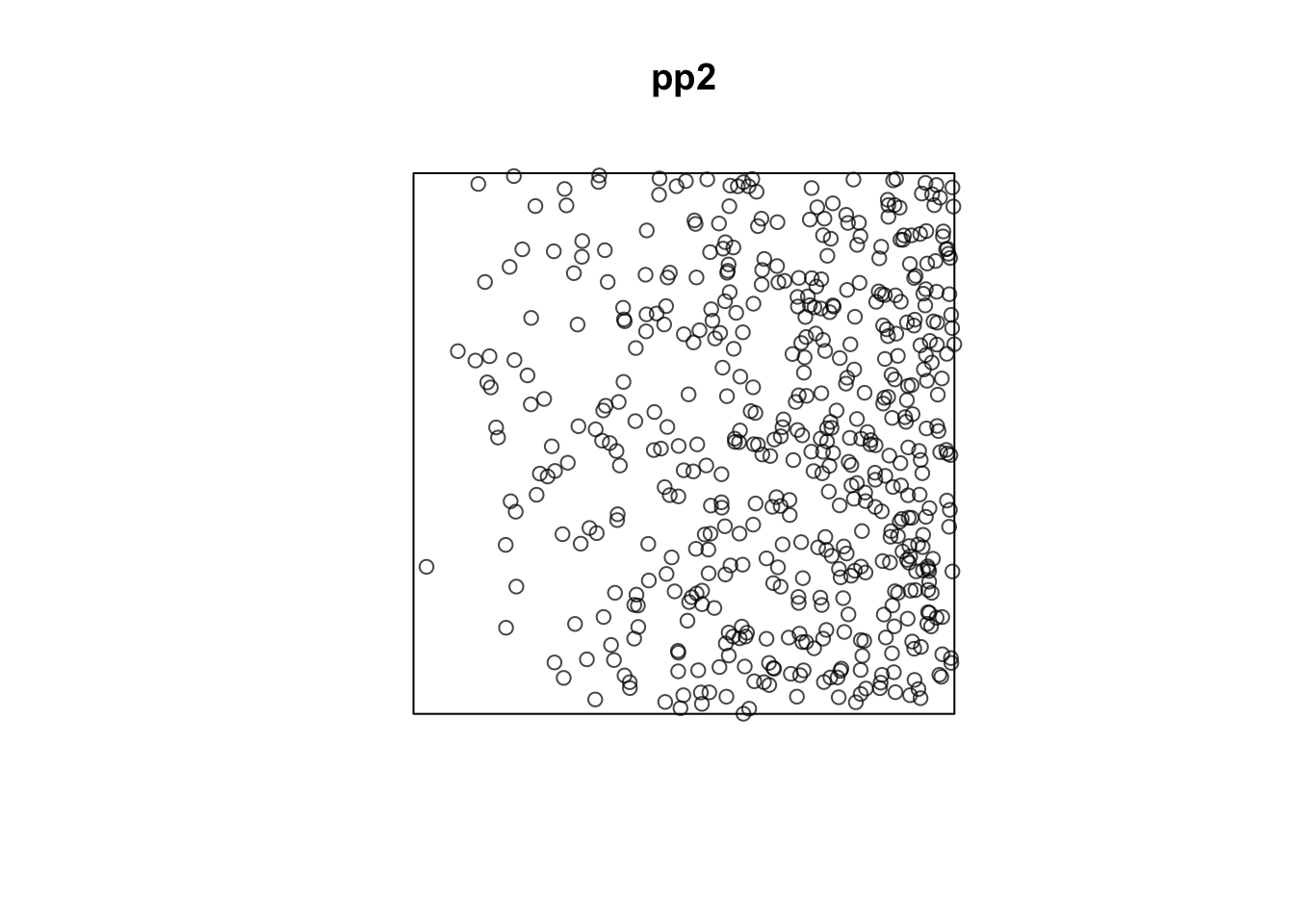
つづいて、図 5.3(b)です。
z <- expand.grid(x = seq(0.5, 99.5, 1),
y = seq(0.5, 99.5, 1))
z$r = (-0.00002 * (z$x - 40)^2 + 0.05) * 0.04 * z$y
z$r[z$r < 0] <- 0
pp3 <- rpoispp(as.im(X = z, W = W))
plot(pp3)
モデルあてはめ
ppm関数で、点過程モデルのあてはめができます。
まず、図 5.2(a)の点配置に、切片だけのモデル(定常ポアソン過程)をあてはめます。
(fit1 <- ppm(pp2 ~ 1))
## Stationary Poisson process
## Fitted to point pattern dataset 'pp2'
## Intensity: 0.0526
## Estimate S.E. CI95.lo CI95.hi Ztest Zval
## log(lambda) -2.945039 0.04360207 -3.030498 -2.859581 *** -67.54356図 5.2(a)の点配置と、図 5.3(b)の点配置との関係をみてみます。
そのためまず、図 5.3(b)の点配置から、カーネル平滑化強度を生成してピクセルイメージに変換します。
Zimage <- density(pp3) |>
as.im()
plot(Zimage)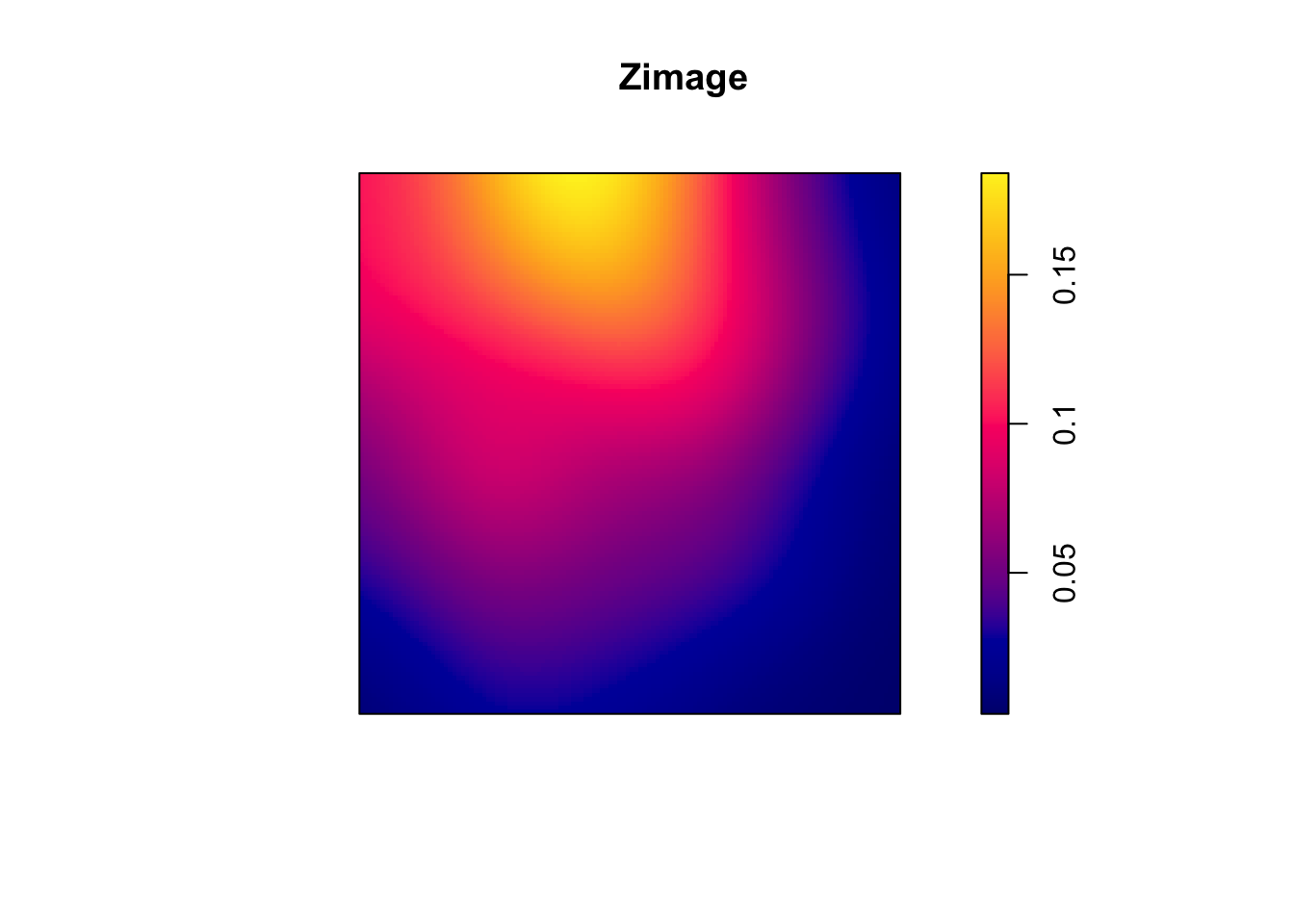
このピクセルイメージを説明変数とした非定常ポアソン過程のモデルを、図 5.2(a)の点配置にあてはめます。
(fit2 <- ppm(pp2 ~ Z, covariates = list(Z = Zimage)))
## Nonstationary Poisson process
## Fitted to point pattern dataset 'pp2'
##
## Log intensity: ~Z
##
## Fitted trend coefficients:
## (Intercept) Z
## -2.468267 -7.955534
##
## Estimate S.E. CI95.lo CI95.hi Ztest Zval
## (Intercept) -2.468267 0.07575967 -2.616753 -2.319781 *** -32.580222
## Z -7.955534 1.15373139 -10.216806 -5.694262 *** -6.895482Zの係数は負なので、両者の点配置は排他的な傾向にあると推測されます。実際、5.3(a)は右側で密度が高く、5.3(b)は低くなっています。
最後に、定常ポアソン過程のモデルと、5.3(b)から生成したカーネル平滑化強度を説明変数としたモデルとでAICを比較します。
AIC(fit1)
## [1] 4152.181
AIC(fit2)
## [1] 4102.039fit2の方がAICが小さくなっています。
L関数
空間点パターンの解析によくもちいられるL関数もspatstatパッケージ(の関連パッケージのspatstat.explore)に入っていますので、これも使ってみます。
まず、定常ポアソン過程で生成したpp1に適用します。
envelope(pp1, Lest) |>
plot(. - r ~ r)
## Generating 99 simulations of CSR ...
## 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
## 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40,
## 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60,
## 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80,
## 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98,
## 99.
##
## Done.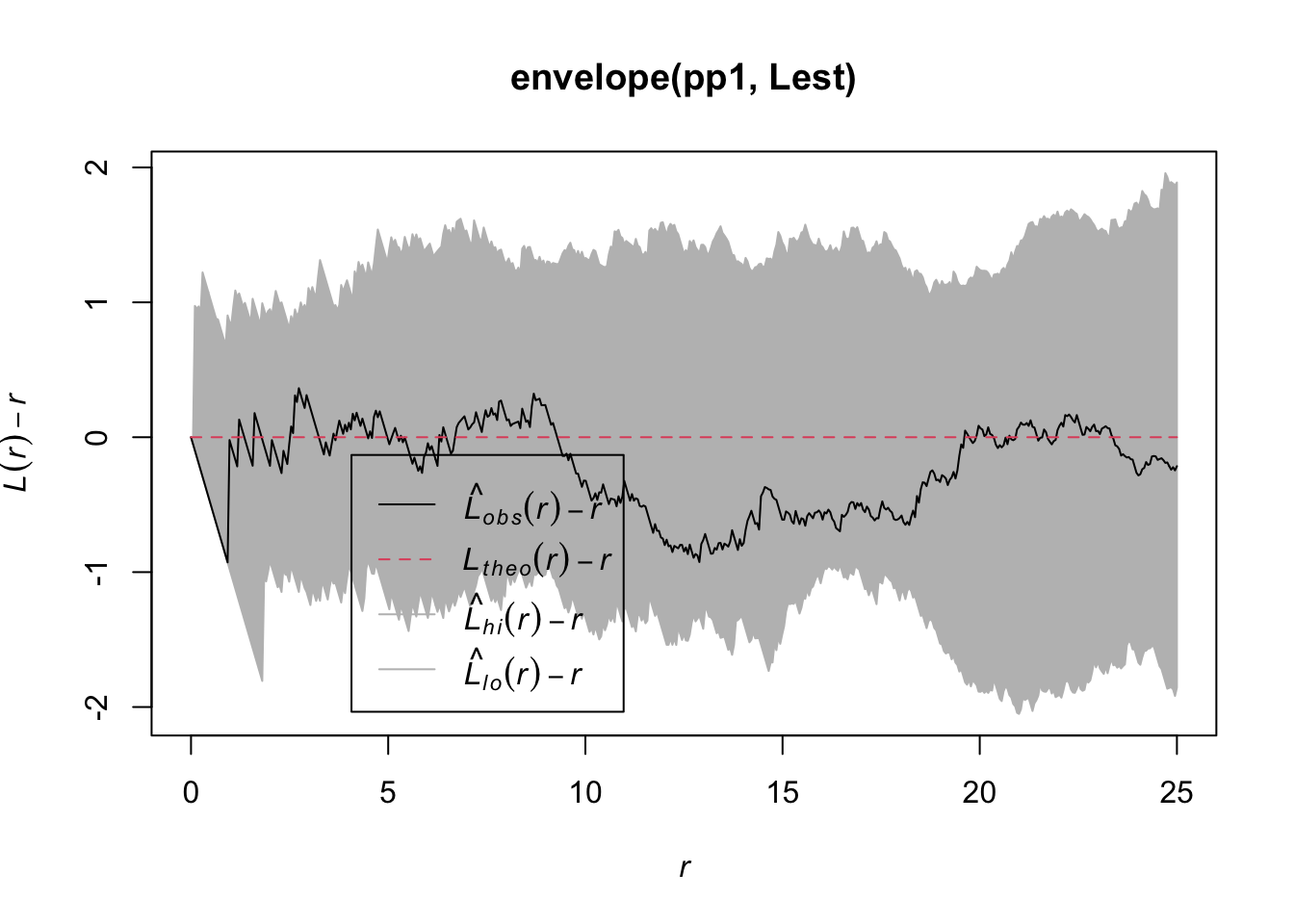
エンベロープにおさまっています。
つぎに、非定常ポアソン過程で生成したpp2です。
envelope(pp2, Lest) |>
plot(. - r ~ r)
## Generating 99 simulations of CSR ...
## 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
## 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40,
## 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60,
## 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80,
## 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98,
## 99.
##
## Done.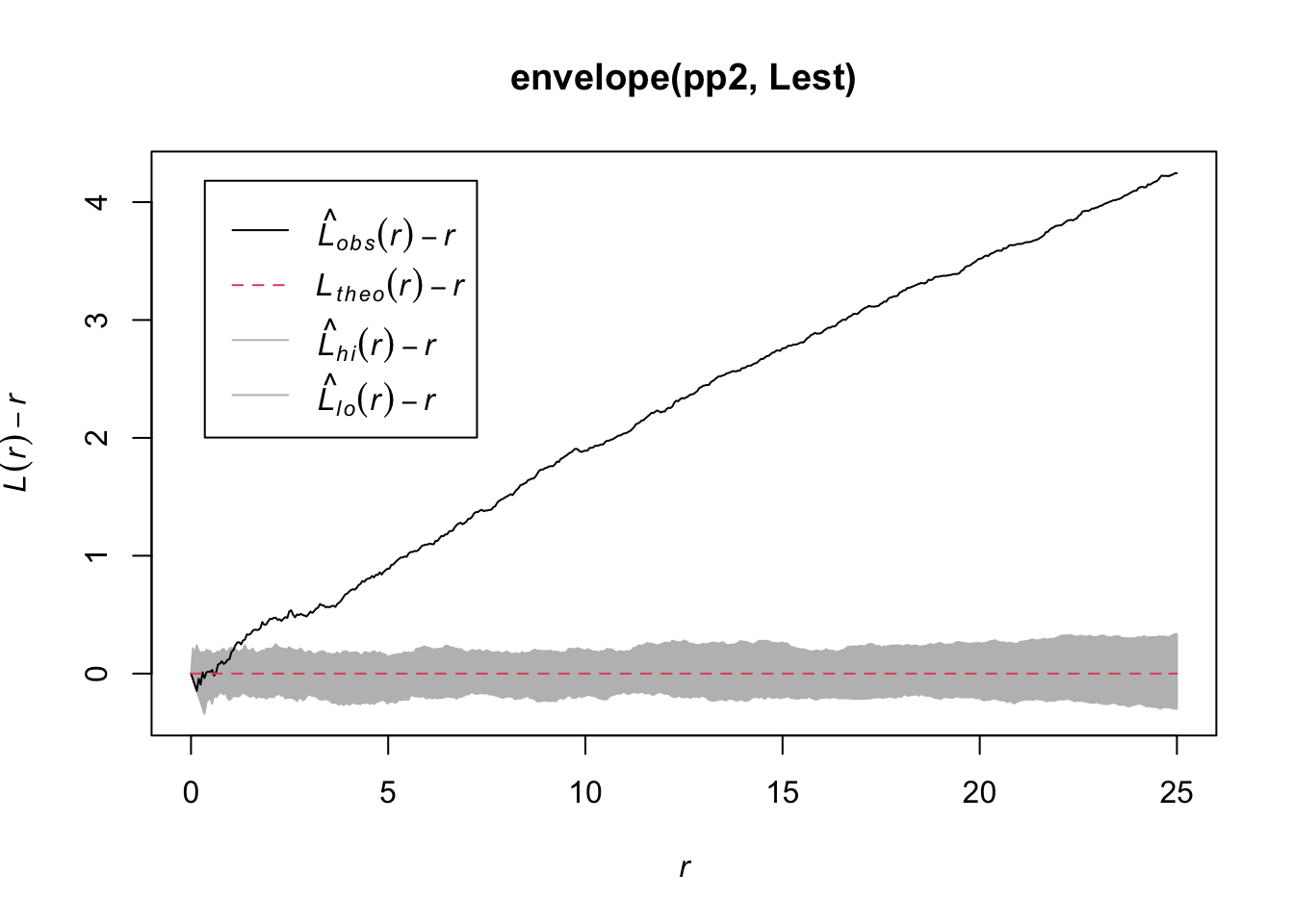
集中分布なので、上におおきくはずれています。
最後にpp2とpp3を比較します。両者を結合して、マークをつけてから、Lcross関数を適用しています。
ppu <- superimpose(pp2, pp3) |>
setmarks(factor(rep(c("pp2", "pp3"), c(pp2$n, pp3$n))))
plot(envelope(ppu, Lcross), . - r ~ r)
## Generating 99 simulations of CSR ...
## 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
## 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40,
## 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60,
## 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80,
## 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98,
## 99.
##
## Done.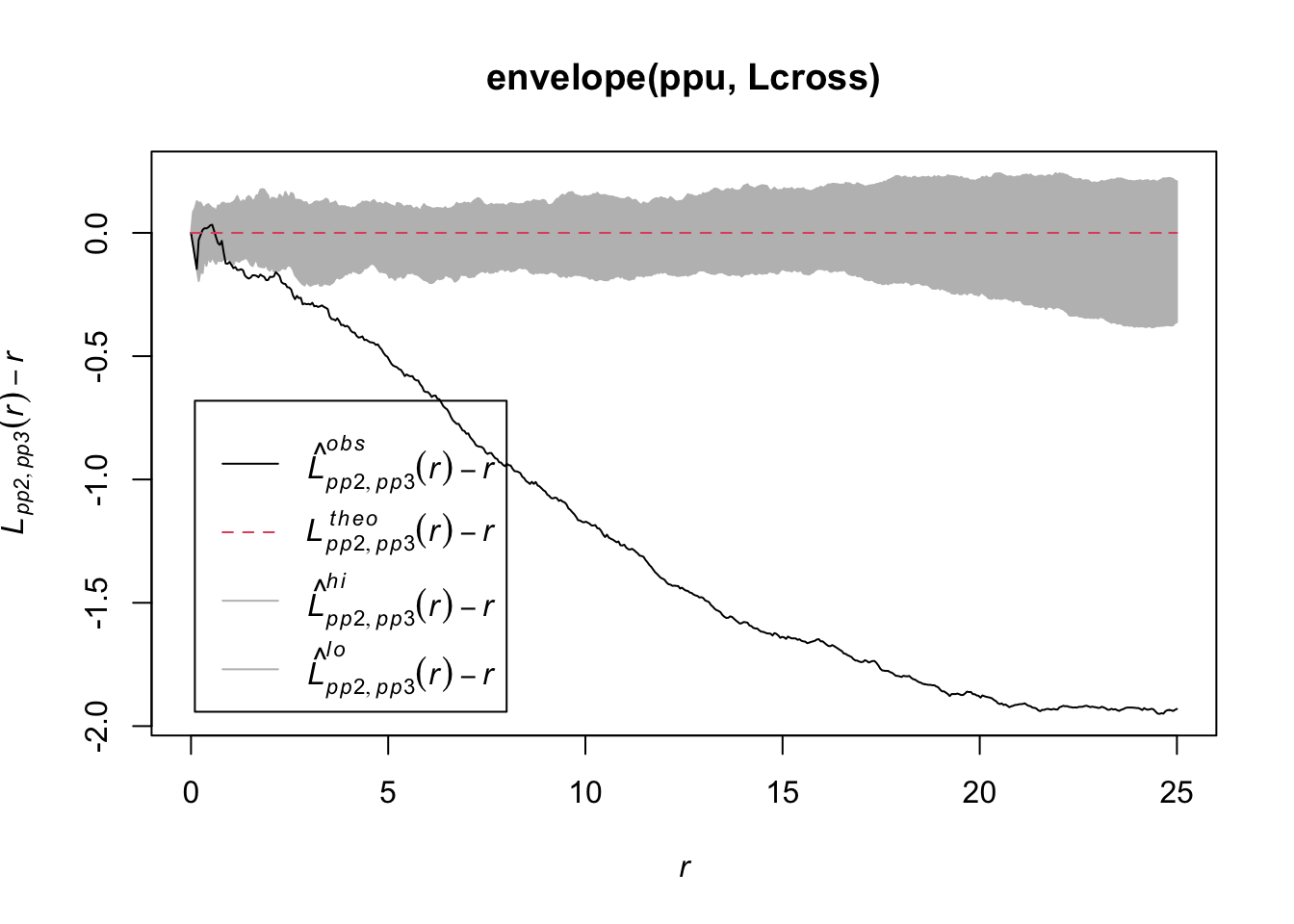
排他的な分布ということで、下におおきくはずれています。