TMBで、打ちきりデータへのモデルのあてはめ

TMBを使って、打ちきりデータへのモデルのあてはめをやってみます。Stan User’s GuideのCensored Dataの項の内容をTMBに移植したような内容になっています。

【2025-08-23 追記】Blueskayでコメントをいただきまして、誤りを修正しました。あと、最適化計算中にsigmaが0以下になる可能性を考慮して、念のため、モデルのパラメータとしてはlog_sigmaを使うようにしました。

データ

模擬データを生成します。平均10、標準偏差4の正規分布で、6以下の値が打ち切られて欠損値になっているという状況を想定しています。

set.seed(123)
N <- 240
mu <- 10
sigma <- 4
cens <- 6
Y <- rnorm(N, mu, sigma)

平均と標準偏差を見てみます。

mean(Y)
## [1] 9.978479
sd(Y)
## [1] 3.753209

打ちきり閾値以下の値を欠損値にしたものをY2とします。

Y2 <- ifelse(Y <= cens, NA, Y)

欠損値の数は以下のようになっています。

length(Y[is.na(Y2)])
## [1] 37

打ちきりを考慮せず、単純に欠損値を除いた平均と標準偏差の値です。打ちきりにより、平均は大きく、標準偏差は小さくなっています。

mean(Y2, na.rm = TRUE)
## [1] 10.95027
sd(Y2, na.rm = TRUE)
## [1] 3.198584

ヒストグラム

ヒストグラムを見てみます。青緑が打ち切られた部分になります。

library(ggplot2)

data.frame(Y = Y, censored = (Y <= cens)) |>
  ggplot(aes(x = Y, fill = censored)) +
  geom_histogram(binwidth = 1, center = 0.5, na.rm = TRUE) +
  theme_minimal()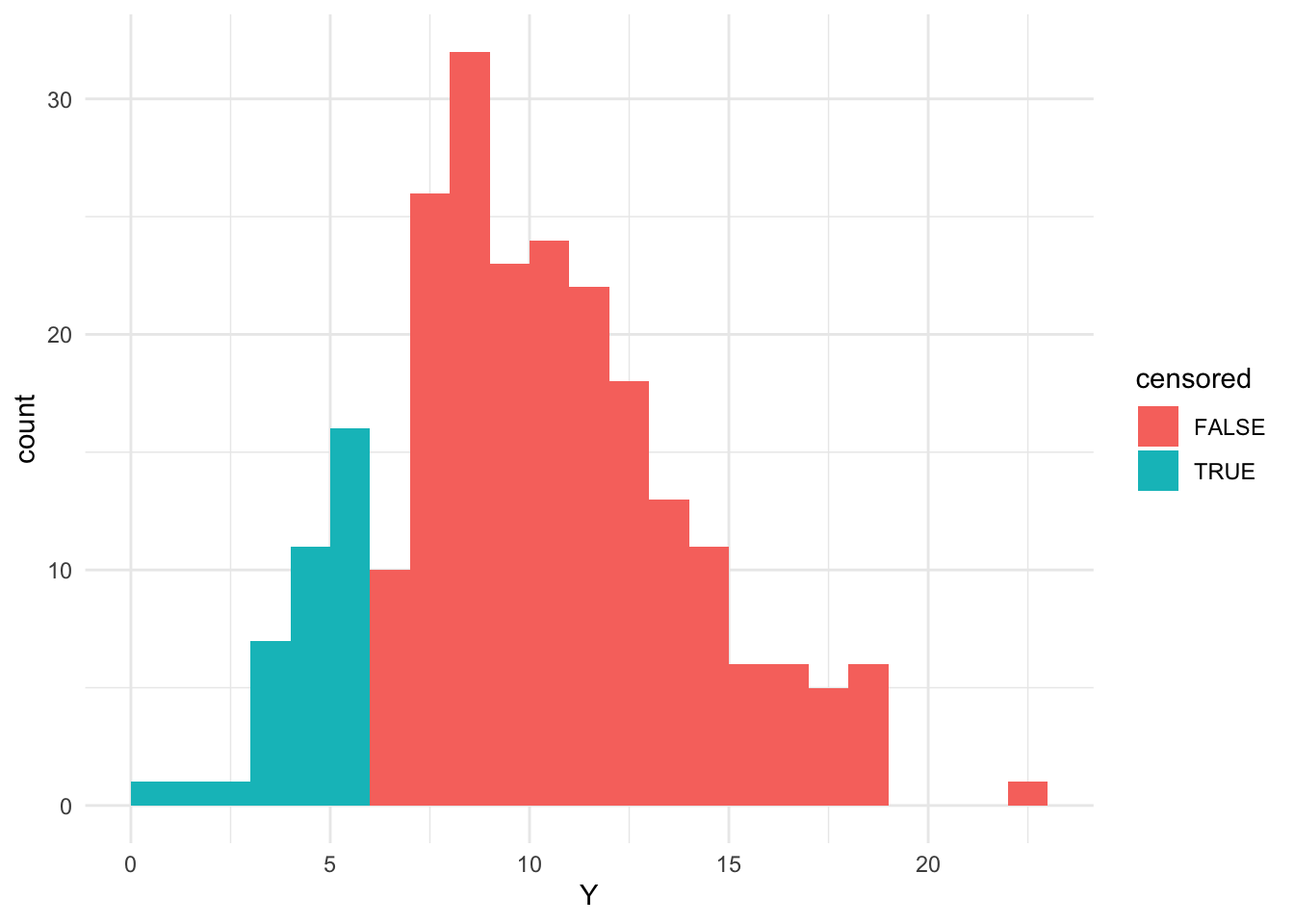

モデル

TMBのC++のコードです。"models/censored.cpp"に保存しておきます。TMBのpnorm関数は、Rのpnormと同様に、正規分布の累積分布関数です。TMBのdnormには、対数で値を返すかどうかを指定するgive_log引数があるのですが、pnormにはありません（ドキュメント）。試してみたところ、~~対数で値を返すようになっていました~~対数ではなく、確率スケールで値を返していました。

censored.cpp

// Censored data
#include <TMB.hpp>

template<class Type>
Type objective_function<Type>::operator() ()
{
  DATA_VECTOR(Y_obs);
  DATA_SCALAR(L);
  DATA_INTEGER(N_cens);
  PARAMETER(mu);
  PARAMETER(log_sigma);
  Type sigma = exp(log_sigma);
  Type nll = 0;

  nll += -sum(dnorm(Y_obs, mu, sigma, true));
  nll += -N_cens * log(pnorm(L, mu, sigma));
  return nll;
}

コンパイルと最適化

モデルをコンパイルして、できたライブラリをロードします。

library(TMB)

model_name <- "censored"
file.path("models", paste(model_name, "cpp", sep = ".")) |>
  compile()
file.path("models", dynlib(model_name)) |>
  dyn.load()

MakeADFun関数で、最適化関数に渡すオブジェクトを作成して、nlminb関数で最適化します。

data <- list(Y_obs = Y2[!is.na(Y2)], L = cens,
             N_cens = sum(is.na(Y2)))
parameters <- list(mu = 1, log_sigma = 0)
obj <- MakeADFun(data, parameters, DLL = model_name)
## Constructing atomic pnorm1
opt <- nlminb(obj$par, obj$fn, obj$gr)
## outer mgc:  21962.24 
## outer mgc:  2766.439 
## outer mgc:  2015.442 
## outer mgc:  627.6762 
## outer mgc:  329.3835 
## outer mgc:  51.0817 
## outer mgc:  24.05909 
## outer mgc:  28.33266 
## outer mgc:  6.86779 
## outer mgc:  4.248491 
## outer mgc:  0.8034103 
## outer mgc:  0.1025161 
## outer mgc:  0.002068856 
## outer mgc:  0.0004122294 
## outer mgc:  1.15373e-05

結果

結果です。convergenceが0なので、収束しているようです。log_sigmaの最尤推定値が1.37なので、sigmaのスケールでは3.94くらいです。muもsigmaも、打ちきりを考慮しない場合よりも、元の値に近くなっていました。

print(opt)
## $par
##        mu log_sigma 
##  9.865439  1.372054 
## 
## $objective
## [1] 606.2088
## 
## $convergence
## [1] 0
## 
## $iterations
## [1] 14
## 
## $evaluations
## function gradient 
##       15       15 
## 
## $message
## [1] "relative convergence (4)"