TMBによる標準距離標本抽出法データの解析

『生態学のための階層モデリング』第8章の標準距離標本抽出法(conventional distance sampling)で採取したデータの解析は、Stanによるベイズ推定をこれまで2回ばかりやっているのですが（[1][2]）、今回はTMBで最尤推定をやってみました。

準備

まずは、パッケージを読み込み擬似乱数のシードを設定します。

library(TMB)
library(ggplot2)
set.seed(123)

データ

インパラのデータを使用します（本の405ページ）。長さ60kmのトランセクトで観測されたインパラのまでの距離(m)です。

このデータからトランセクト内のインパラの個体数を推定します。

X <- c(71.93, 26.05, 58.47, 92.35, 163.83, 84.52, 163.83, 157.33,
       22.27, 72.11, 86.99, 50.8, 0, 73.14, 0, 128.56, 163.83, 71.85,
       30.47, 71.07, 150.96, 68.83, 90, 64.98, 165.69, 38.01, 378.21,
       78.15, 42.13, 0, 400, 175.39, 30.47, 35.07, 86.04, 31.69, 200,
       271.89, 26.05, 76.6, 41.04, 200, 86.04, 0, 93.97, 55.13, 10.46,
       84.52, 0, 77.65, 0, 96.42, 0, 64.28, 187.94, 0, 160.7, 150.45,
       63.6, 193.19, 106.07, 114.91, 143.39, 128.56, 245.75, 123.13,
       123.13, 153.21, 143.39, 34.2, 96.42, 259.81, 8.72)

ヒストグラムを表示します。

geom_histogram関数のcenter引数の値を25にするか、24.9にするかで、ぴったり400の値が350〜400に入るか、あるいは400〜500に入るかが変わります。今回は25にして、350〜400の方に入れるようにしました。

ggplot(data.frame(X = X), aes(x = X)) +
  geom_histogram(fill = "blue", binwidth = 50, center = 25) +
  labs(x = "Distance (m)", y = "Frequencty") +
  theme_minimal()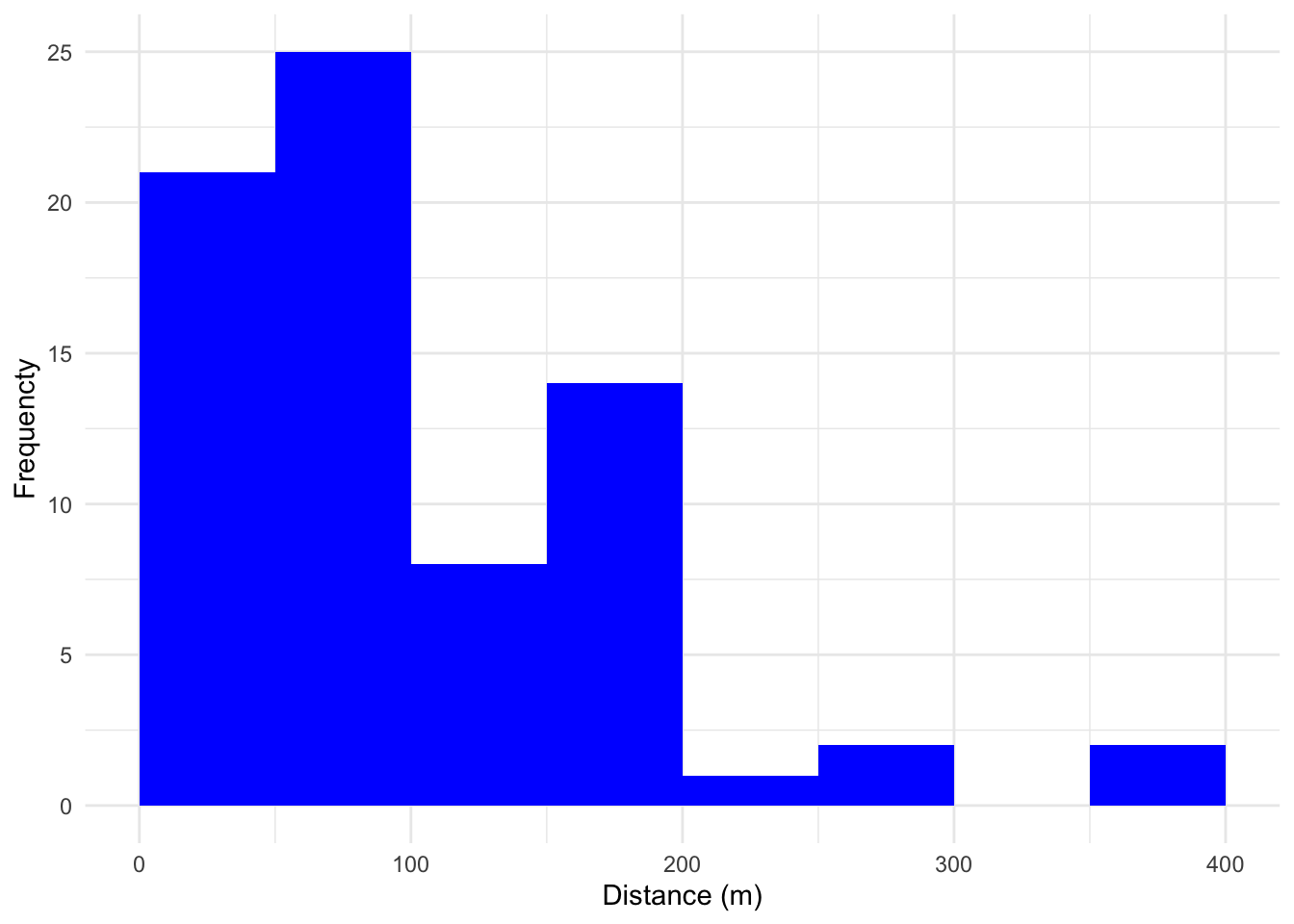

トランセクト幅の半分（片側の範囲）は観測距離の最大より大きく設定するとあります。本と同じく、500mに設定しました。

B <- 500

観測された個体数は以下になります。

(N_obs <- length(X))
## [1] 73

モデル

尤度（完全尤度）の式は以下になります。本とは少し記法を変えています。

\[ L(\sigma, n_0) = \left\{\prod_{i=1}^{n_\mathrm{obs}}\frac{g(x_i;\sigma)[x_i]}{\int g(x;\sigma)[x]dx}\right\} \frac{(n_\mathrm{obs} + n_0)!}{n_\mathrm{obs}!n_0!}\bar{p}^{n_\mathrm{obs}}(1-\bar{p})^{n_0} \]

• \(n_\mathrm{obs}\): 検出された個体数
• \(n_0\): 検出されなかった個体数（パラメータ）
• \(\bar{p}\): 平均検出確率
• \(x_i\): \(i\)番目の検出個体までの距離(m)
• \(g(x;\sigma)\): 距離\(x\)のときの検出確率（\(\sigma\)はパラメータ）
• \([x]\): 距離\(x\)に対する個体の確率密度

距離\(x\)についての個体の確率密度\([x]\)は、半距離\(B\)内での一様分布とします。

\[ [x]=\frac{1}{B} \]

平均検出確率\(\bar{p}\)は以下のようになります。

\[ \bar{p}=\int g(x;\sigma)[x]dx \]

これらから、尤度式は以下のように変形できます。

\[ L(\sigma,n_0)=\frac{(n_\mathrm{obs} + n_0)!}{n_\mathrm{obs}!n_0!}\left\{\prod_{i=1}^{n_\mathrm{obs}}\frac{g(x_i;\sigma)}{B}\right\}(1-\bar{p})^{n_0} \]

検出確率は半正規とします。

\[ g(x;\sigma) = \exp\left(-\frac{x^2}{2\sigma^2}\right) \]

TMBのモデル

尤度をTMBでモデル化します。推定するのは、半正規検出関数の尺度パラメータsigmaと、分布しているが検出されなかった個体数n0です。

4〜8行目で、検出確率の関数gを定義しています。

10〜22行目までは、検出確率の数値積分をおこなう関数integrateを定義しています。シンプソン法を使用しました。

24行目以降はモデルの定義で、完全尤度の式をTMBで記述しています。

cds.cpp

// Conventional distance sampling
#include <TMB.hpp>

template<class Type>
Type g(Type x, Type sigma)
{
  return exp(-(x * x) / (2 * sigma * sigma));
}

template<class Type>
Type integrate(Type a, Type b, Type sigma, int n) {
  if (n % 2 == 1)
    n++;
  Type h = (b - a) / n;
  Type s = g(a, sigma);
  for (int i = 1; i < n; i += 2)
    s += 4 * g(a + i * h, sigma);
  for (int i = 2; i < n; i += 2)
    s += 2 * g(a + i * h, sigma);
  s += g(b, sigma);
  return s * h / 3;
}

template<class Type>
Type objective_function<Type>::operator() ()
{
  DATA_VECTOR(X);
  Type nobs = X.size();
  DATA_SCALAR(B);
  PARAMETER(log_sigma);
  Type sigma = exp(log_sigma);
  PARAMETER(log_n0);
  Type n0 = exp(log_n0);
  Type nll = Type(0);
  
  Type pbar = integrate(Type(0), B, sigma, 100) / B;
  nll += -(lgamma(nobs + n0 + 1) - lgamma(nobs + 1) - lgamma(n0 + 1));
  for (int i = 0; i < nobs; i++)
    nll += -(log(g(X(i), sigma)) - log(B));
  nll += -(n0 * log(1 - pbar));
  return nll;
}

コンパイルして、ライブラリを読み込みます。

model_name <- "cds"
file.path("models", paste(model_name, "cpp", sep = ".")) |>
  compile()
## Note: Using Makevars in /Users/hiroki/.R/Makevars
## using C++ compiler: 'Apple clang version 17.0.0 (clang-1700.0.13.5)'
## using SDK: ''
## [1] 0
dynlib(file.path("models", model_name)) |>
  dyn.load()

データとパラメータ初期値を用意して、最適化計算を実行します。

data <- list(X = X, B = B)
parameters <- list(log_sigma = log(100), log_n0 = log(100))
obj <- MakeADFun(data, parameters, DLL = model_name)
## Constructing atomic D_lgamma
opt <- nlminb(obj$par, obj$fn, obj$gr)
## outer mgc:  87.31944 
## outer mgc:  6.68936 
## outer mgc:  3.187166 
## outer mgc:  1.080715 
## outer mgc:  0.6073467 
## outer mgc:  0.1929046 
## outer mgc:  0.001288947 
## outer mgc:  1.123285e-05

結果

結果を表示します。convergenceが0なので、無事収束しました。

print(opt)
## $par
## log_sigma    log_n0 
##  4.859366  5.026393 
## 
## $objective
## [1] 410.3982
## 
## $convergence
## [1] 0
## 
## $iterations
## [1] 7
## 
## $evaluations
## function gradient 
##       10        8 
## 
## $message
## [1] "relative convergence (4)"

対数値を通常のスケールに戻すと、sigmaは128.9、n0は152.4になります。

したがって、トランセクト内の総個体数は225.4、密度はこれを60×0.5×2=60で割って、 3.76頭/km²と推定されました。

本にある、ベイズ推定での結果とだいたいあっているようです。