金沢市のクマ出没予測マップの作成

「クマ共生ハッカソン」の一環として、小松市のクマ出没予測マップに続いて、金沢市の予測マップを作成しました。基本的な構造は小松市のものと同様です。RのsdmTMBパッケージを使用して、時空間自己相関を組み込んだ種分布モデル（Species Distribution Model: SDM）を作成し、予測をおこないました。

データ

前回と同様に、クマ出没情報は、いしかわオープンデータカタログの「石川県クマ出没データ」からダウンロードしたものに前処理を加えたものを使用します。国土数値情報の土地利用3次メッシュデータ、行政区域データも同じです。

以下のRコードでは、tidyverse, sf, nanoparquet, sdmTMBの各パッケージを読み込み、データファイルの場所を指定しています。ここも前回と同様です。

library(tidyverse)
## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr     1.1.4     ✔ readr     2.1.5
## ✔ forcats   1.0.0     ✔ stringr   1.5.1
## ✔ ggplot2   3.5.2     ✔ tibble    3.3.0
## ✔ lubridate 1.9.4     ✔ tidyr     1.3.1
## ✔ purrr     1.1.0     
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag()    masks stats::lag()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
library(sf)
## Linking to GEOS 3.13.0, GDAL 3.8.5, PROJ 9.5.1; sf_use_s2() is TRUE
library(nanoparquet)
library(sdmTMB)

# データディレクトリ
data_dir <- "data"

# クマ出没データ
data_file <- file.path(data_dir, "kuma_data.parquet")

# 土地利用データ
landuse_files <- 
  c("L03-a-21_5436.geojson",
    "L03-a-21_5536.geojson",
    "L03-a-21_5537.geojson",
    "L03-a-21_5636.geojson",
    "L03-a-21_5637.geojson") |>
  purrr::map_chr(~ file.path(data_dir, .x))

# 石川県行政区域データ
ishikawa_pref_file <- file.path(data_dir, "N03-20250101_17.geojson")

クマ出没データ

Parquet形式で保存しておいたクマ出没データを読み込みます。土地利用データにあわせて、500mメッシュコードから3次（1km）メッシュコードを作成しておきます。ここも前回と同様です。

kuma_data <- read_parquet(data_file) |>
  # 3次メッシュコード
  # 500mメッシュコードの先頭から8文字
  dplyr::mutate(mesh_code = str_sub(`500mメッシュコード`, 1, 8))

土地利用データ

土地利用データを読み込みます。データ中の各土地利用面積はm²単位ですが、km²単位に変換します。また、3次メッシュコードを文字型に変換しておきます。ここも前回とまったく同じです。

landuse <- landuse_files %>%
  purrr::map(\(f) {
    sf::st_read(f, quiet = TRUE)
  }) |>
  dplyr::bind_rows() |>
  # m^2単位をkm^2単位にする
  dplyr::mutate_at(2:14, `/`, 10^6) |>
  # 3次メッシュコードを文字型にする
  dplyr::mutate(mesh_code = as.character(`メッシュ`))

行政区域データ

国土数値情報の石川県の行政区域データを読み込み、金沢市の行政区域を抽出します。

kanazawa <- sf::st_read(ishikawa_pref_file, quiet = TRUE) |>
  dplyr::filter(N03_004 == "金沢市") |>
  sf::st_union()

土地利用3次メッシュのうち金沢市の行政区域と重なるものを抽出します。

int <- sf::st_intersects(landuse, kanazawa, sparse = FALSE)
landuse_kanazawa <- landuse[int, ]

クマ出没情報の地図

金沢市のクマ出没データについて、3次メッシュごと年ごとの出没情報のありなしを集計して、p_sumに格納します。

p_sum <- kuma_data |>
  dplyr::filter(`市町名` == "金沢市") |>
  dplyr::rename(year = `出没年`) |>
  dplyr::group_by(mesh_code, year) |>
  dplyr::summarise(present = as.numeric(n() > 0),
                   .groups = "drop")

6年間（2019〜2024年）で、3次メッシュごとにクマの出没情報があった年の割合を地図でしめします。

geometry <- landuse_kanazawa |>
  dplyr::select(mesh_code, geometry)

prop <- p_sum |>
  dplyr::group_by(mesh_code) |>
  dplyr::summarise(prop = n() / 6, .groups = "drop")

geometry |>
  dplyr::left_join(prop, by = "mesh_code") |>
  dplyr::mutate(prop = replace_na(prop, 0)) |>
  ggplot(aes(fill = prop)) +
  geom_sf() +
  scale_fill_viridis_c(name = "割合") +
  theme_minimal(base_family = "Noto Sans JP")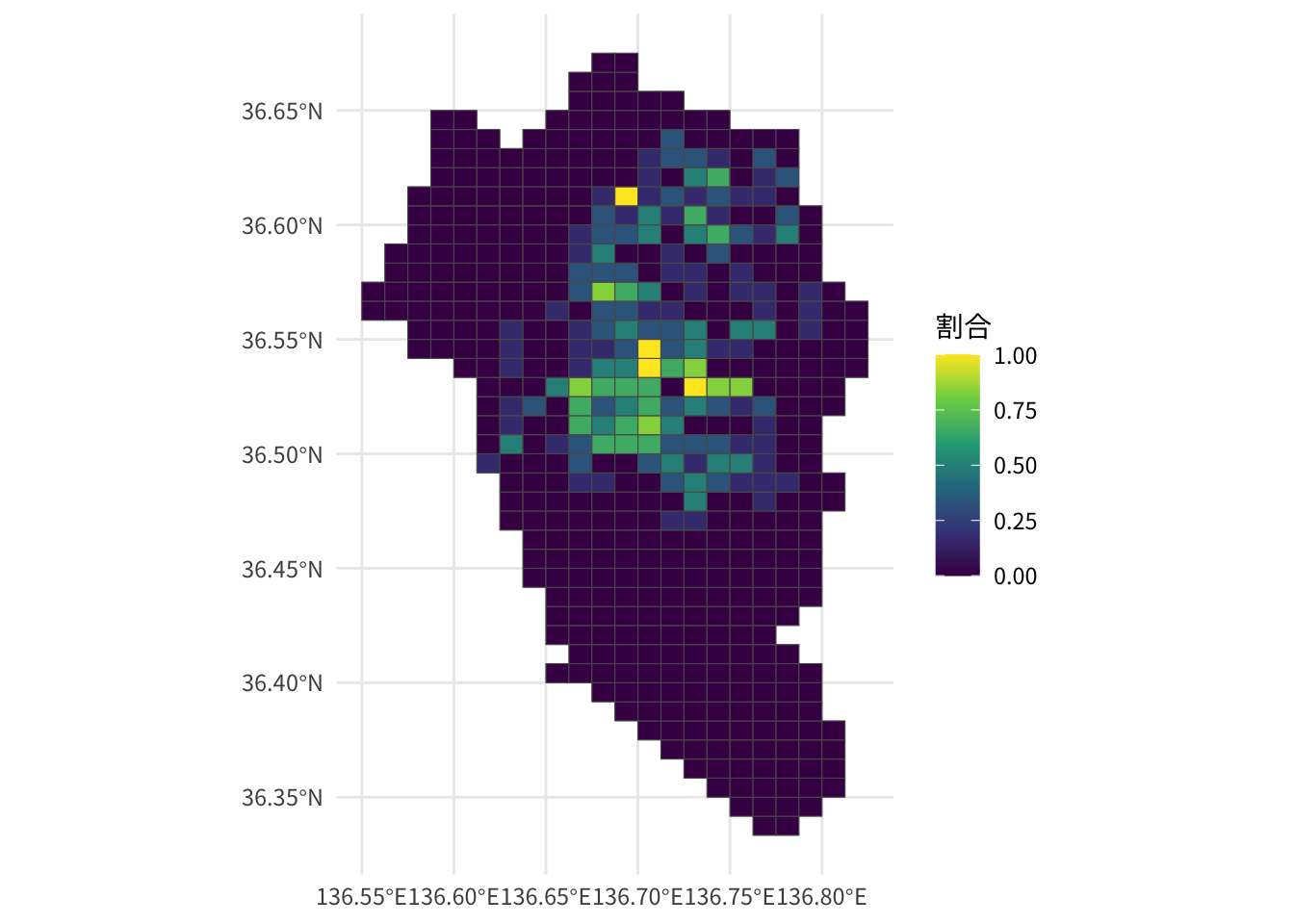

図 1: 金沢市の３次メッシュごとの、クマの出没情報があった年の割合（2019〜2024年）

土地利用との関係

土地利用との関係を確認します。まず、3次メッシュ中の森林面積とクマ出没頻度（割合）との関係を見てみます。

land_prop <- landuse_kanazawa |>
  dplyr::left_join(prop, by = "mesh_code") |>
  tidyr::replace_na(list(prop = 0))
ggplot(land_prop, aes(x = `森林`, y = prop)) +
  geom_point(color = "red", size = 2.5) +
  labs(title = "金沢市における、3次メッシュ中の森林面積とクマ出没頻度との関係",
       x = expression(paste("森林面積(", km^2, ")")),
       y = "出没があった年の割合") +
  theme_bw(base_family = "Noto Sans JP")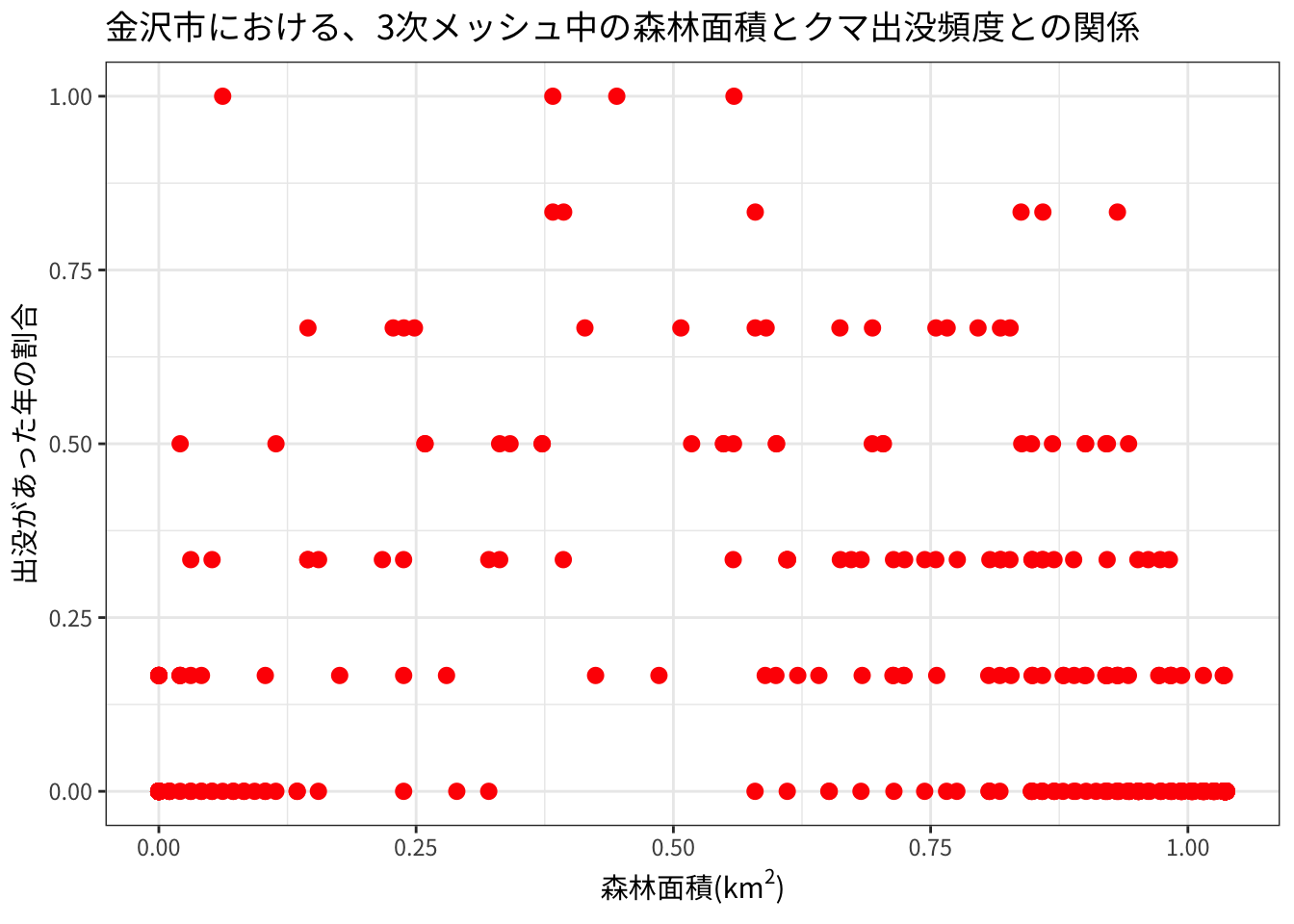

やはり、森林面積の割合が中間くらいのところで出没頻度が高そうです。

同様に、河川地及び湖沼面積についても見てみます。

land_prop <- landuse_kanazawa |>
  dplyr::left_join(prop, by = "mesh_code") |>
  tidyr::replace_na(list(prop = 0))
ggplot(land_prop, aes(x = `河川地及び湖沼`, y = prop)) +
  geom_point(color = "red", size = 2.5) +
  labs(title = "金沢市における、河川地及び湖沼面積とクマ出没頻度との関係",
       x = expression(paste("河川地及び湖沼面積(", km^2, ")")),
       y = "出没があった年の割合") +
  theme_bw(base_family = "Noto Sans JP")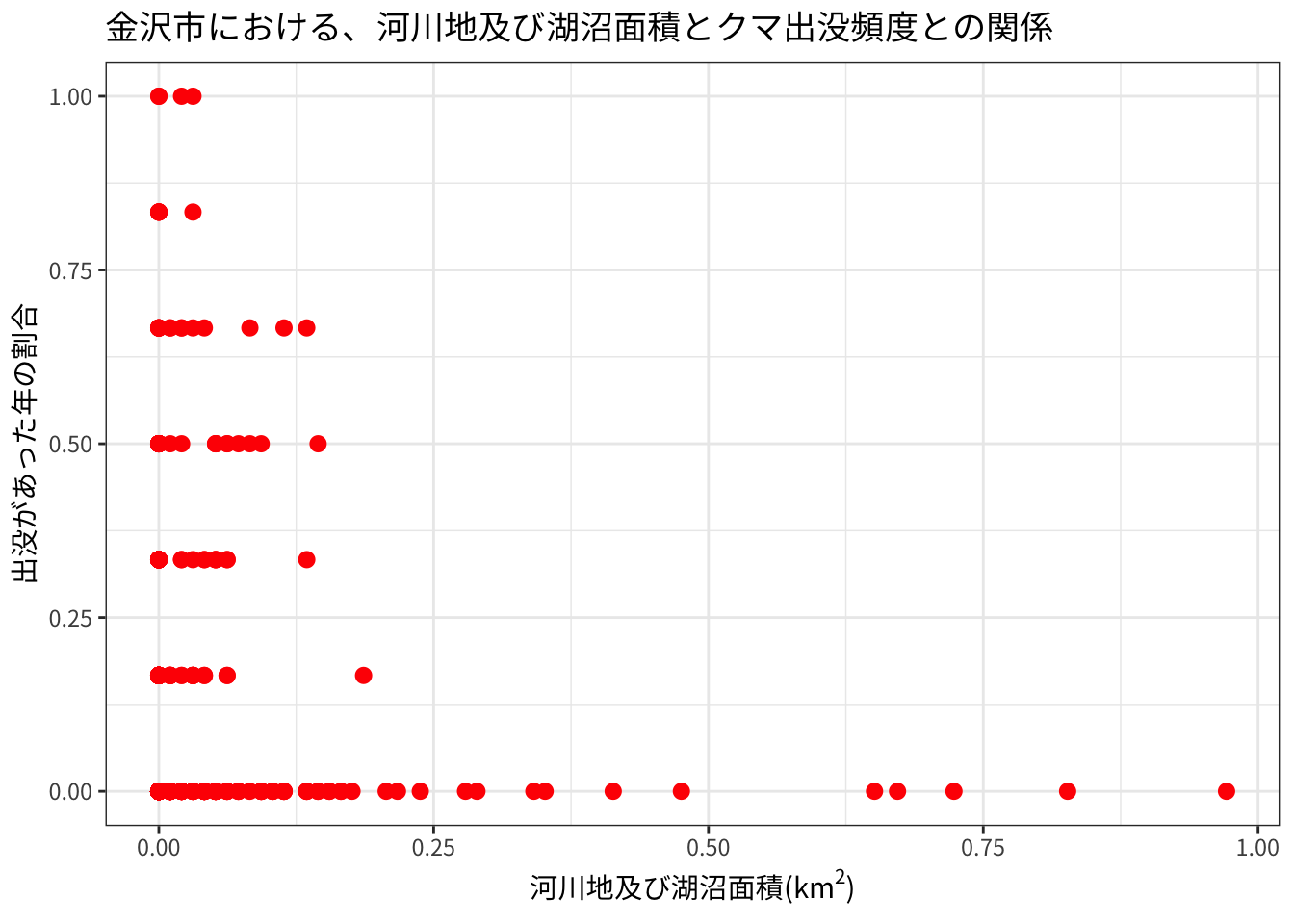

こちらは、割合が小さいほど出没頻度が高そうですが、河川・湖沼でないということよりも、森林や市街地ということを反映した結果の可能性もありそうです。

統計モデル

全出没タイプを統合したデータについて、出没情報のありなしをモデル化します。ここからも基本的には前回と同じです。

説明変数として用いる可能性のある環境データとして以下を用意しました。

forest: 3次メッシュ中の森林面積(km²)
forest2: 3次メッシュ中の森林面積(km²)の2乗
water: 3次メッシュ中の河川地及び湖沼面積(km²)
water2: 3次メッシュ中の河川地及び湖沼面積(km²)の2乗

env <- landuse_kanazawa |>
  dplyr::mutate(forest = `森林`,
                forest2 = `森林`^2,
                water = `河川地及び湖沼`,
                water2 = `河川地及び湖沼`^2) |>
  as.data.frame() |>
  dplyr::select(mesh_code, forest, forest2, water, water2)

3次メッシュコードと年のすべての組み合わせをつくっておき、これに出没のありなしデータと環境データを結合させます。

同時に、ブナ豊凶をしめすダミー変数buna_poorを加えます。大凶作の年（2020年）は1、それ以外の年は0をとります。

p_year <- tidyr::expand_grid(
  mesh_code = unique(landuse_kanazawa$mesh_code),
  year = 2019:2024
) |>
  dplyr::left_join(p_sum, by = c("mesh_code", "year")) |>
  dplyr::mutate(present = replace_na(present, 0)) |>
  dplyr::left_join(env, by = "mesh_code") |>
  dplyr::mutate(buna_poor = if_else(year == 2020, 1, 0))

sdmTMBで使用するメッシュ作成のため、UTM座標系の座標を求めます。landuse_kanazawaの座標系をWGS84 (EPSG: 4326)に変換します。各メッシュの重心の座標を求め、これからさらに対応するUTM座標系(53N)を求めています。

coord <- landuse_kanazawa |>
  sf::st_transform(4326) |>
  sf::st_make_valid() |>
  sf::st_centroid() |>
  sf::st_coordinates() |>
  as.data.frame() |>
  dplyr::rename(longitude = X, latitude = Y) |>
  add_utm_columns(ll_names = c("longitude", "latitude"))

出没あり・なしデータに経度・緯度データを結合します。

coord2 <- coord |>
  bind_cols(
    landuse_kanazawa |>
      dplyr::select(mesh_code)
    )
p_year_coord <- p_year |>
  dplyr::left_join(coord2, by = "mesh_code")

メッシュの作成

sdmTMBで使用するメッシュを作成します。辺の最小の長さ(cutoff)も、小松市のときと同様に2kmとしました。

mesh <- make_mesh(p_year_coord, xy_cols = c("X", "Y"), cutoff = 2)
plot(mesh)

モデルの作成とあてはめ

こちらも前回と同じく、2種類のモデルを用意しました。

森林面積(F)とその2乗、河川・湖沼面積(W)、ブナの豊凶(B, 大凶作: 1, それ以外0)を説明変数とするモデル
森林面積(F)とその2乗、ブナの豊凶を説明変数とするモデル

ともに、これら説明変数のほかに、空間自己相関をモデルに組み込んでいます。前回との違いとして、今回は年変化をモデルに組み込んでも、年変化の効果が0と推定されてしまいましたので、年の効果は抜いてあります。

目的変数Yはクマ出没情報のあり(Y=1)、なし(Y=0)とします。Yは、確率pのベルヌーイ分布にしたがうとします。

\[ Y \sim \mathrm{Bernoulli}(p) \]

確率pは、そのロジットlogit(p)が、線形予測子（以下の式はモデル1の線形予測子）と、空間の変量効果（\(\epsilon\)）の和に等しいとします。

\[ \mathrm{logit}(p) = \beta + \beta_\mathrm{F} F + \beta_\mathrm{F2}F^2 + \beta_\mathrm{W}W + \beta_\mathrm{B}B + \epsilon \]

sdmTMB関数を使用して、それぞれのモデルをあてはめます。空間の変量効果はガウスランダム場にしたがうとしています。

これらの環境要因以外の要因（誘引物など）は、ガウスランダム場としてメッシュに割り当てることを想定しています。

以下のRコードのモデル式では、forestは森林面積（モデル式ではF）、waterは河川・湖沼面積（モデル式ではW）、buna_poor（モデル式ではB）はブナ大凶作の年かどうかを示すダミー変数（1: 大凶作、0: 大凶作以外）です。

fit1 <- sdmTMB(present ~ forest + forest2 + water + buna_poor,
              data = p_year_coord,
              mesh = mesh,
              family = binomial(link = "logit"),
              spatial = "on")
fit2 <- sdmTMB(present ~ forest + forest2 + buna_poor,
              data = p_year_coord,
              mesh = mesh,
              family = binomial(link = "logit"),
              spatial = "on")

結果

あてはめ結果をチェックします。モデル1です。

sanity(fit1)
## ✔ Non-linear minimizer suggests successful convergence
## ✔ Hessian matrix is positive definite
## ✔ No extreme or very small eigenvalues detected
## ✔ No gradients with respect to fixed effects are >= 0.001
## ✔ No fixed-effect standard errors are NA
## ✔ No standard errors look unreasonably large
## ✔ No sigma parameters are < 0.01
## ✔ No sigma parameters are > 100
## ✔ Range parameter doesn't look unreasonably large

モデル2です。

sanity(fit2)
## ✔ Non-linear minimizer suggests successful convergence
## ✔ Hessian matrix is positive definite
## ✔ No extreme or very small eigenvalues detected
## ✔ No gradients with respect to fixed effects are >= 0.001
## ✔ No fixed-effect standard errors are NA
## ✔ No standard errors look unreasonably large
## ✔ No sigma parameters are < 0.01
## ✔ No sigma parameters are > 100
## ✔ Range parameter doesn't look unreasonably large

どちらも問題は見つかりませんでした。

AICを比較します。

c(AIC(fit1), AIC(fit2))
## [1] 1316.213 1314.383

AICの値はモデル2の方が多少小さく、またモデル2の方がより単純なモデルですので、より予測能力が高いモデルとしてモデル2を採用します。

2つのモデルのあてはめの結果の要約を表示します。

summary(fit1)
## Spatial model fit by ML ['sdmTMB']
## Formula: present ~ forest + forest2 + water + buna_poor
## Mesh: mesh (isotropic covariance)
## Data: p_year_coord
## Family: binomial(link = 'logit')
##  
## Conditional model:
##             coef.est coef.se
## (Intercept)    -6.24    2.29
## forest          8.26    1.44
## forest2        -8.29    1.17
## water          -1.01    2.50
## buna_poor       1.30    0.18
## 
## Matérn range: 21.29
## Spatial SD: 2.56
## ML criterion at convergence: 651.107
## 
## See ?tidy.sdmTMB to extract these values as a data frame.

summary(fit2)
## Spatial model fit by ML ['sdmTMB']
## Formula: present ~ forest + forest2 + buna_poor
## Mesh: mesh (isotropic covariance)
## Data: p_year_coord
## Family: binomial(link = 'logit')
##  
## Conditional model:
##             coef.est coef.se
## (Intercept)    -6.31    2.31
## forest          8.33    1.43
## forest2        -8.31    1.17
## buna_poor       1.30    0.18
## 
## Matérn range: 21.36
## Spatial SD: 2.58
## ML criterion at convergence: 651.192
## 
## See ?tidy.sdmTMB to extract these values as a data frame.

予測

モデル2を用いて、3次メッシュごとのクマ出没確率を予測します。今年2025年はブナ大凶作の予報ですので、その値を予測します。

newdata <- env |>
  dplyr::left_join(coord2, by = "mesh_code") |>
  dplyr::mutate(buna_poor = 1)
pred_buna_poor <- predict(fit2, newdata, type = "response")

地図で表示します。

pred_buna_poor |>
  sf::st_as_sf() |>
  ggplot(aes(fill = est)) +
  geom_sf() +
  scale_fill_viridis_c(name = "出没確率", limits = c(0, 1)) +
  theme_minimal(base_family = "Noto Sans JP")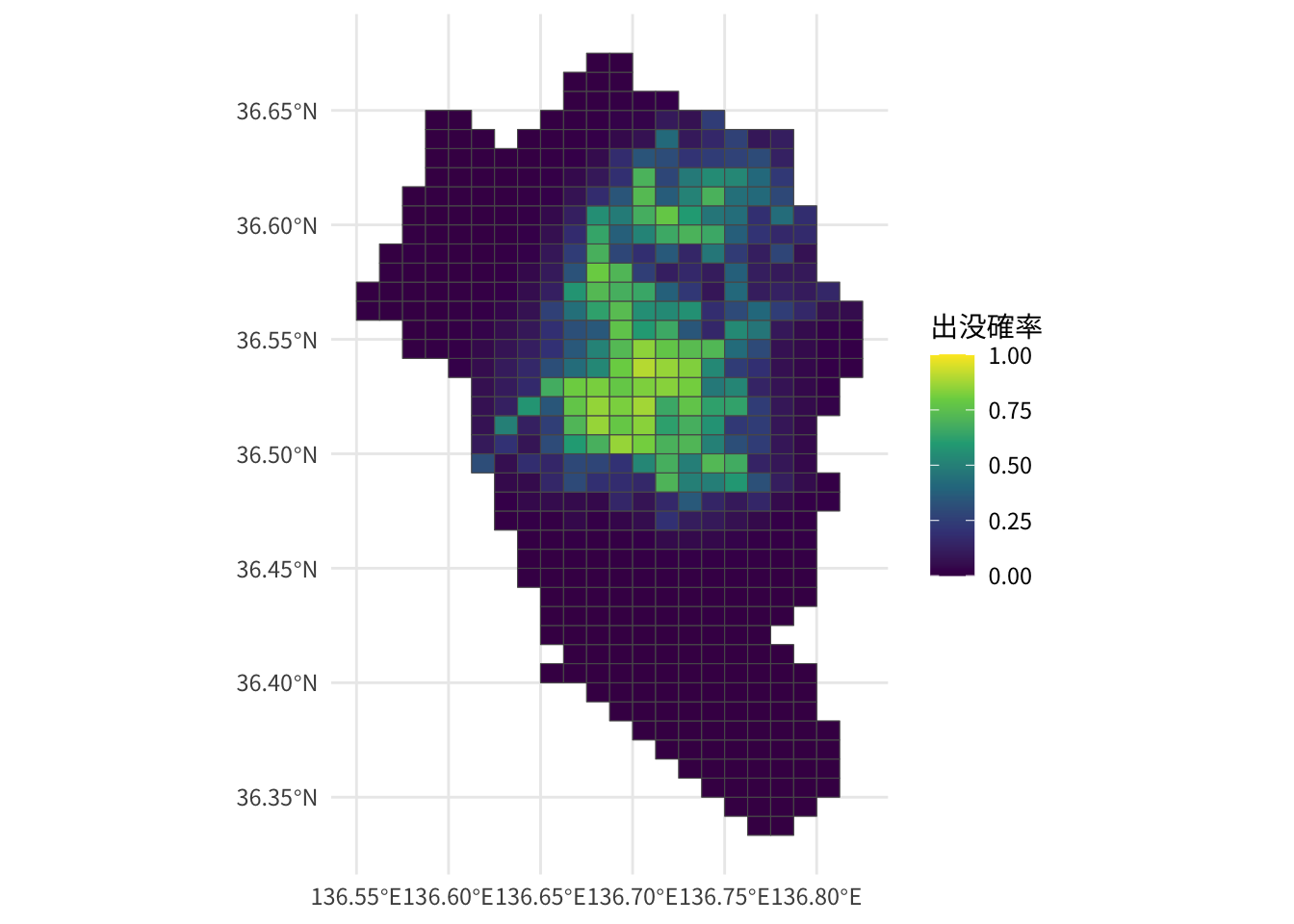

小松市と同様、森林と市街地との境界付近に、出没確率が高いと予測されたメッシュがかなりあります。

おわりに

金沢市についても、クマ出没予測マップを作成しました。

これも前回の繰り返しになりますが、予測マップで出没確率が低いと予測されていても、クマに対する注意は必要です。南部の森林が広がる場所で出没確率が低く予測されているのは、そもそも出没として情報があがってくることがあまりないからで、クマの生息域であることは間違いありません。

クマの生息域に立ち入るときは音を立てて人の存在を知らせるとか、クマの生息しない市街地でも、生ゴミなどの誘引物を放置しないといった基本的な対策をとることは重要です。