library(tidyverse)
## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr 1.1.4 ✔ readr 2.1.5
## ✔ forcats 1.0.0 ✔ stringr 1.5.1
## ✔ ggplot2 3.5.2 ✔ tibble 3.3.0
## ✔ lubridate 1.9.4 ✔ tidyr 1.3.1
## ✔ purrr 1.1.0
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag() masks stats::lag()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
library(sf)
## Linking to GEOS 3.13.0, GDAL 3.8.5, PROJ 9.5.1; sf_use_s2() is TRUE
library(nanoparquet)
library(patchwork)
library(sdmTMB)
# データ配置ディレクトリ
data_dir <- "data"
# クマ出没データのパス
data_file <- file.path(data_dir, "kuma_data.parquet")
# 土地利用データのパス
landuse_files <-
c("L03-a-21_5436.geojson",
"L03-a-21_5536.geojson",
"L03-a-21_5537.geojson",
"L03-a-21_5636.geojson",
"L03-a-21_5637.geojson") |>
purrr::map_chr(\(f) file.path(data_dir, f))
# 石川県行政区域データのパス
ishikawa_pref_file <- file.path(data_dir,
"N03-20250101_17.geojson")
# 擬似乱数のシードの設定
set.seed(1234)「クマ共生ハッカソン」の記事です。これまでに、小松市のクマ出没予測マップと金沢市のクマ出没予測マップを作成しました。今回は範囲を広げて、石川県全体の予測マップを作成することとします。
種分布モデル(SDM)を利用していますが、クマ(ツキノワグマ)そのものの分布予測ではなく、クマ出没の事案が発生する確率の予測になります。予測には、RのsdmTMBパッケージを使用しました。
予測能力の高いモデルが加賀・能登で異なりましたので、別々にマップをつくり、最後にあわせるという処理をおこないました。
データ
いつものとおり、クマ出没情報は、いしかわオープンデータカタログの「石川県クマ出没データ」からダウンロードしたものに前処理を加えたものを使用します。国土数値情報の土地利用3次メッシュデータ、行政区域データも同じく使用します。
まず、Rパッケージの読み込みとデータファイルのパスの設定、擬似乱数のシードの設定をおこないます。
データ読み込み
データを読み込みます。
# クマ出没データの読み込み
kuma_data <- read_parquet(data_file) |>
# 500mメッシュコードを3次(1km)メッシュコードに変換
dplyr::mutate(mesh_code = str_sub(`500mメッシュコード`, 1, 8))
# 土地利用データの読み込み
landuse_data <- landuse_files %>%
purrr::map(\(f) {
sf::st_read(f, quiet = TRUE)
}) |>
dplyr::bind_rows() |>
# m^2単位をkm^2単位にする
dplyr::mutate_at(2:14, `/`, 10^6) |>
# 3次メッシュコードを文字型にする
dplyr::mutate(mesh_code = as.character(`メッシュ`))
# 地域名の定義
region <- c("Kaga", "Noto")
# 石川県の行政区域データの読み込み
ishikawa <- sf::st_read(ishikawa_pref_file, quiet = TRUE)
# 各地域の市町名を格納するリスト
city <- vector("list", 2)
# 加賀地方(かほく市以南)の市町を抽出
city[["Kaga"]] <- ishikawa |>
dplyr::filter(N03_004 %in% c("金沢市", "小松市", "加賀市", "かほく市",
"白山市", "能美市", "野々市市", "川北町",
"津幡町", "内灘町")) |>
sf::st_union()
# 能登地方(宝達志水町以北)の市町を抽出
city[["Noto"]] <- ishikawa |>
dplyr::filter(N03_004 %in% c("輪島市", "珠洲市", "穴水町",
"能登町", "七尾市", "羽咋市",
"志賀町", "宝達志水町",
"中能登町")) |>
sf::st_union()データの集計・整形
クマ出没データについて、3次メッシュコードと年ごとにクマ出没情報の有無と件数を集計します。
kuma_sum <- kuma_data |>
dplyr::rename(year = `出没年`) |>
dplyr::group_by(mesh_code, year) |>
dplyr::summarise(present = as.numeric(n() > 0),
n = n(),
.groups = "drop")予測モデル作成のため、データを整形します。
まず、土地利用データのうち加賀地方・能登地方に重なる部分をそれぞれ抽出します。
landuse <- purrr::map(
region, \(r) {
intersects <- sf::st_intersects(landuse_data, city[[r]], sparse = FALSE)
landuse_data[intersects, ]
})
names(landuse) <- region土地利用データから、3次メッシュコードと地理情報だけを抽出したデータを作成します。
geometry <- purrr::map(
region, \(r) {
landuse[[r]] |>
dplyr::select(mesh_code, geometry)
})
names(geometry) <- region3次メッシュコードごとに、6年間の出没ありの年の割合を計算します。
prop_app <- kuma_sum |>
dplyr::group_by(mesh_code) |>
dplyr::summarise(prop = n() / 6, .groups = "drop")データ可視化
出没年の割合の地図化
3次メッシュコードごとの、6年間の出没ありの年の割合を地図として可視化します。
そのための関数を定義します。
plot_prop <- function(region, title) {
geometry[[region]] |>
dplyr::left_join(prop_app, by = "mesh_code") |>
dplyr::mutate(prop = replace_na(prop, 0)) |>
ggplot(aes(fill = prop)) +
geom_sf() +
scale_fill_viridis_c(name = "割合", limits = c(0, 1)) +
labs(title = title) +
theme_minimal(base_family = "Noto Sans JP")
}加賀地方と能登地方の出現割合の地図を並べて描画します。
p1 <- plot_prop("Kaga", "加賀地方")
p2 <- plot_prop("Noto", "能登地方")
p2 / p1 + plot_layout(guides = "collect")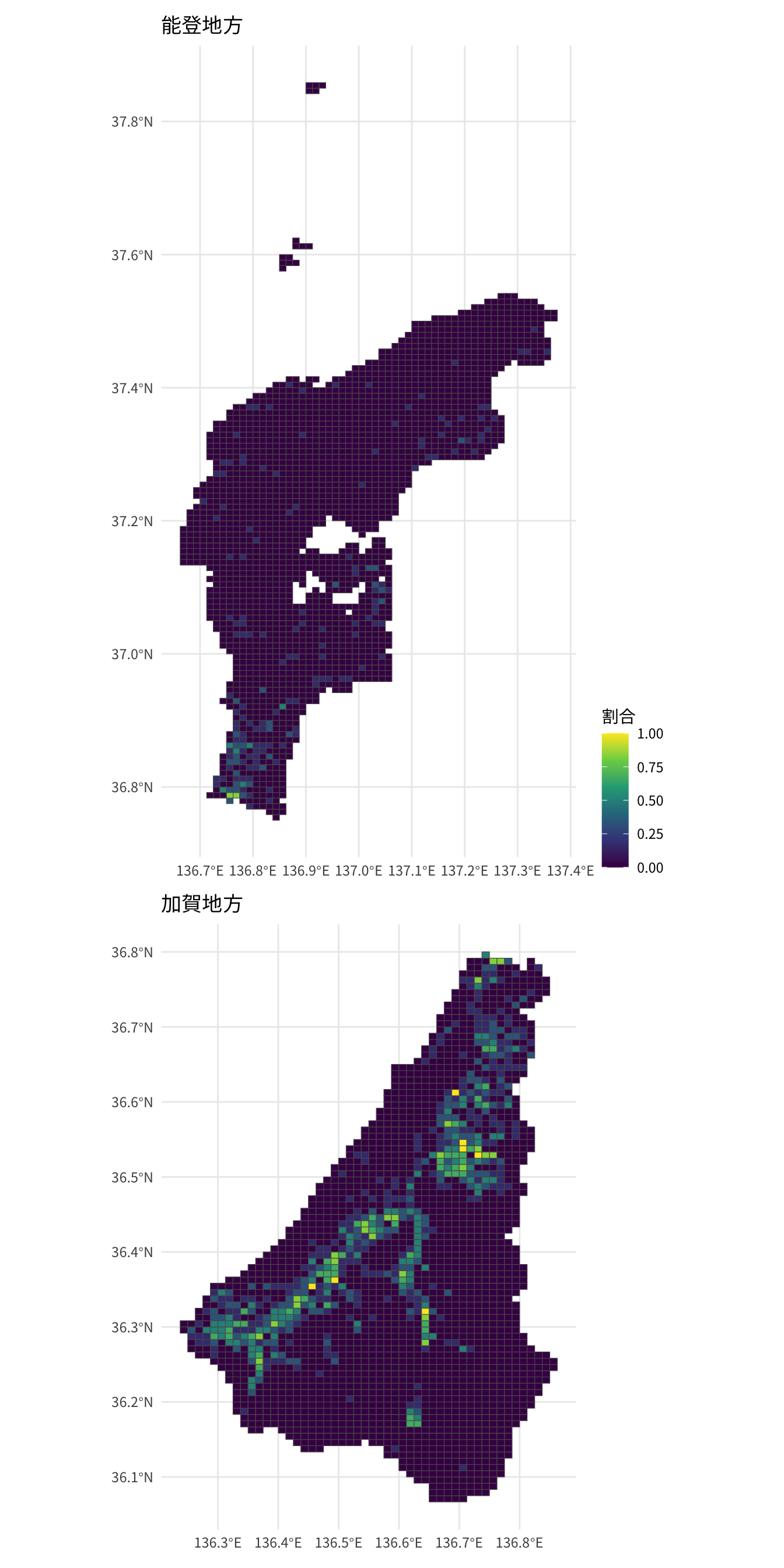
土地利用との関係
土地利用データと出没割合データを結合して、両者の関係を図示します。
そのための関数を定義します。
plot_landuse_prop <- function(region, type,
title = NULL, xlab = NULL,
ylab = "割合") {
landuse[[region]] |>
dplyr::left_join(prop_app, by = "mesh_code") |>
tidyr::replace_na(list(n = 0, prop = 0)) |>
ggplot(aes(x = .data[[type]], y = prop)) +
geom_point(color = "red", size = 2.5) +
geom_smooth(method = "gam") +
labs(title = title, x = xlab, y = ylab) +
theme_bw(base_family = "Noto Sans JP")
}加賀地方: 森林面積と出没割合
加賀地方における、3次メッシュ中の森林面積とクマ出没のあった年の割合との関係です。青い線はGAMによる平滑化線、灰色の領域はその95%信頼区間です(以下同じ)。
plot_landuse_prop("Kaga", "森林",
x = expression(paste("森林面積(", km^2, ")")))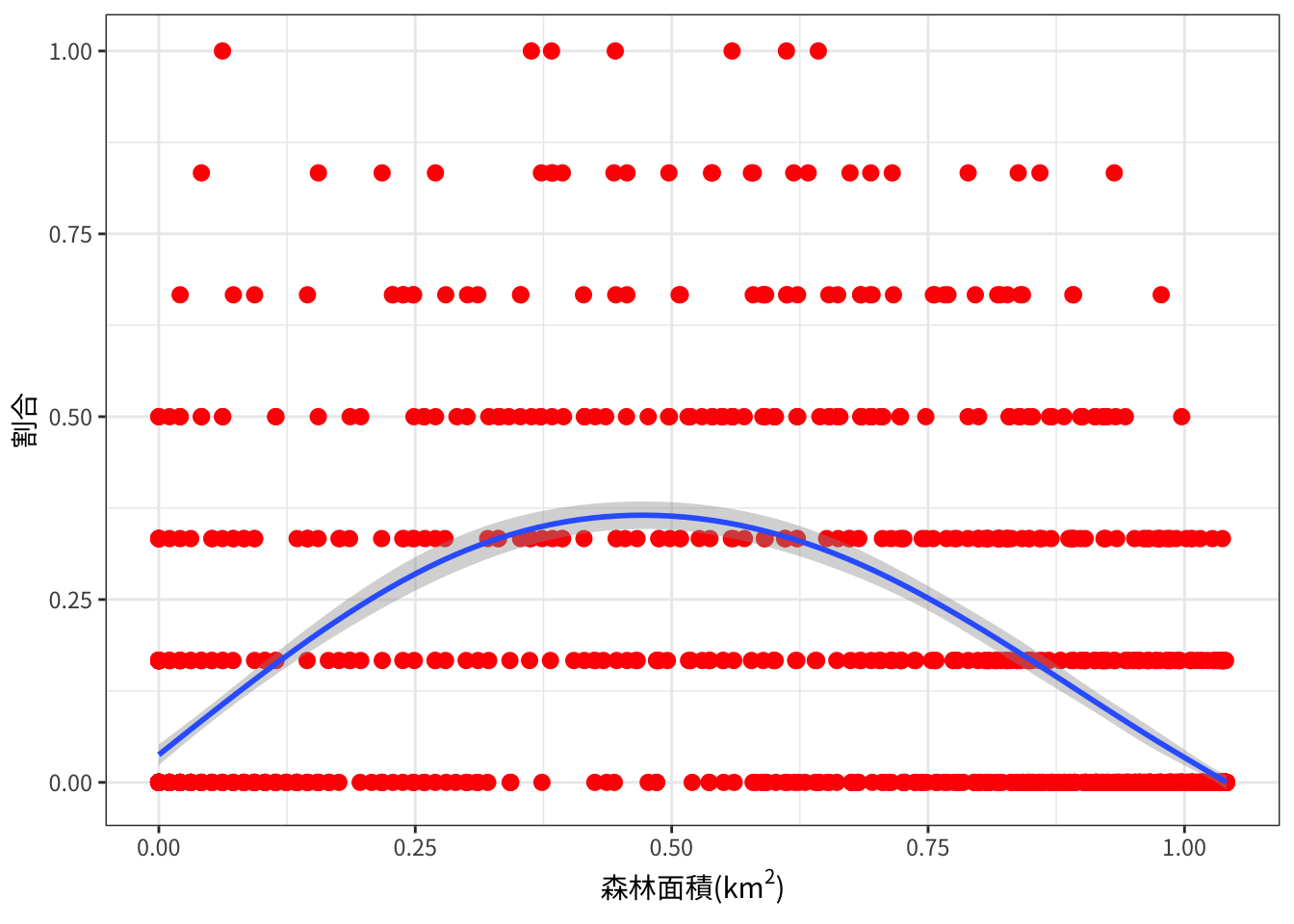
森林面積が中くらいのところで出現割合が高くなっているようです。
加賀地方: 河川地及び湖沼面積と出没割合
つづいて、加賀地方における、3次メッシュ中の河川地及び湖沼面積とクマ出没頻度との関係です。
plot_landuse_prop("Kaga", "河川地及び湖沼",
x = expression(paste("河川地及び湖沼面積(", km^2, ")")))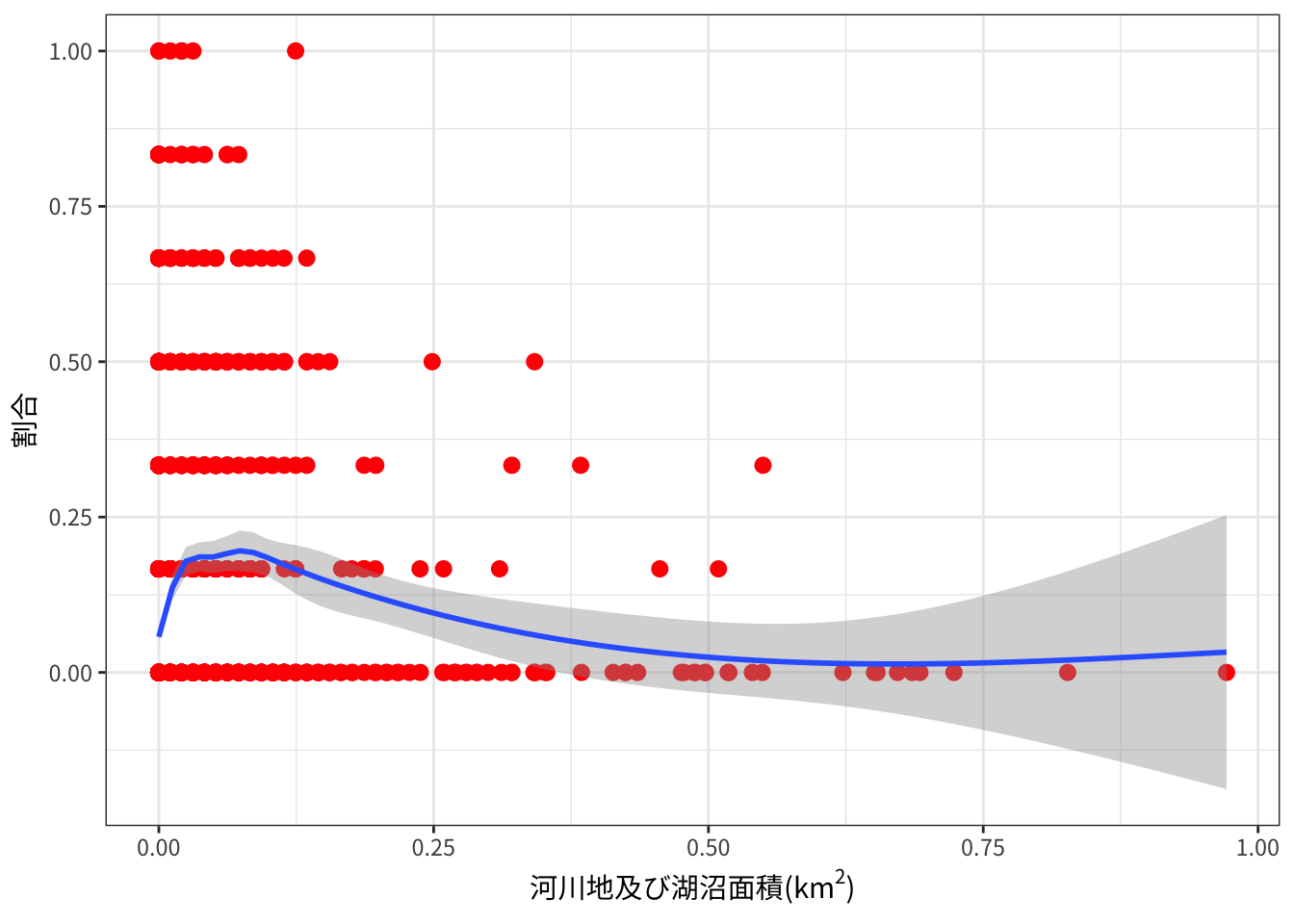
能登地方: 森林面積と出没割合
能登地方における、3次メッシュ中の森林面積とクマ出没のあった年の割合との関係です。
plot_landuse_prop("Noto", "森林",
x = expression(paste("森林面積(", km^2, ")")))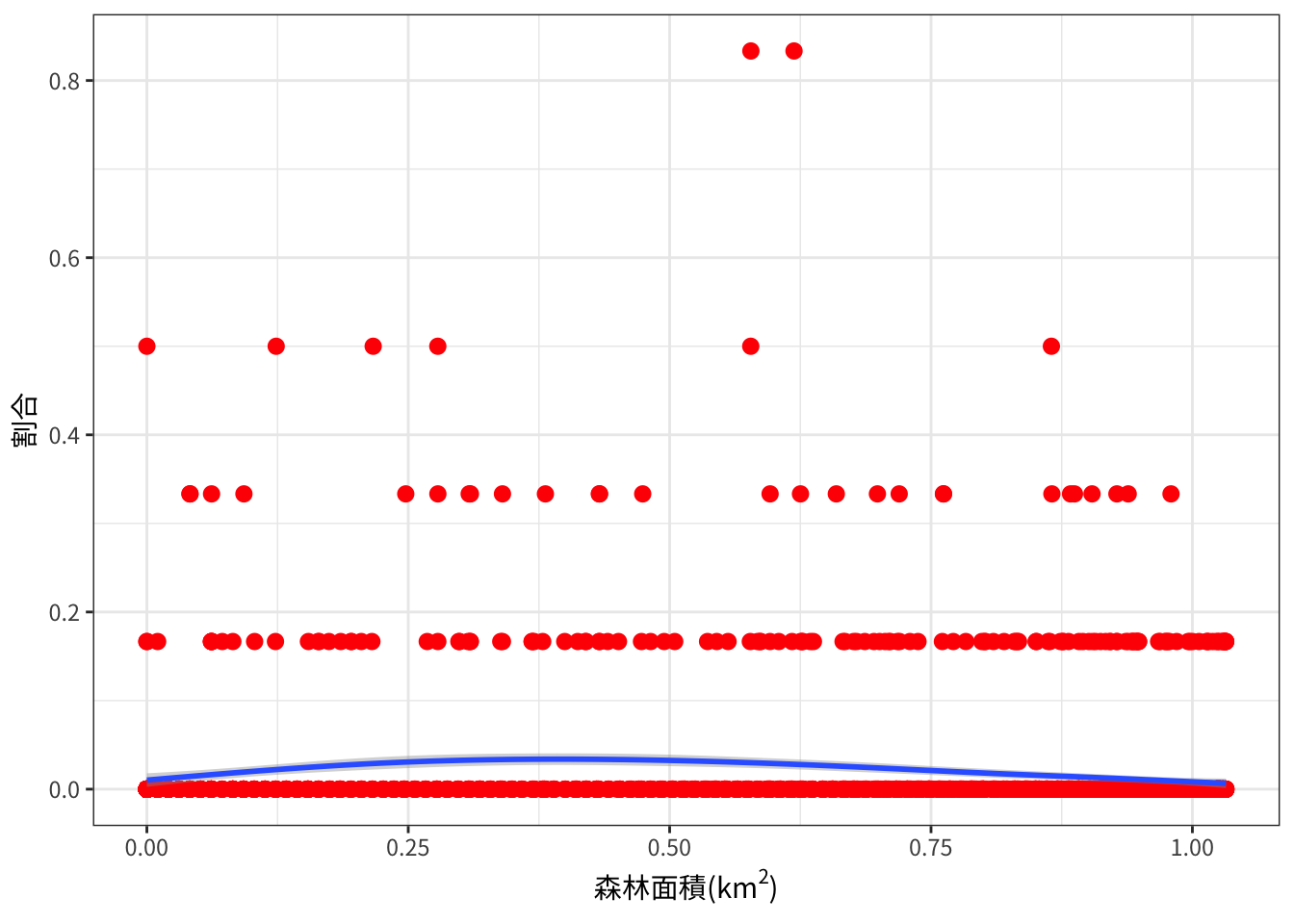
森林面積が0.38km2くらいのところで出現割合がやや高くなっているようです。
能登地方: 河川地及び湖沼面積と出没割合
能登地方における、3次メッシュ中の河川地及び湖沼面積とクマ出没頻度との関係です。
plot_landuse_prop("Noto", "河川地及び湖沼",
x = expression(paste("河川地及び湖沼面積(", km^2, ")")))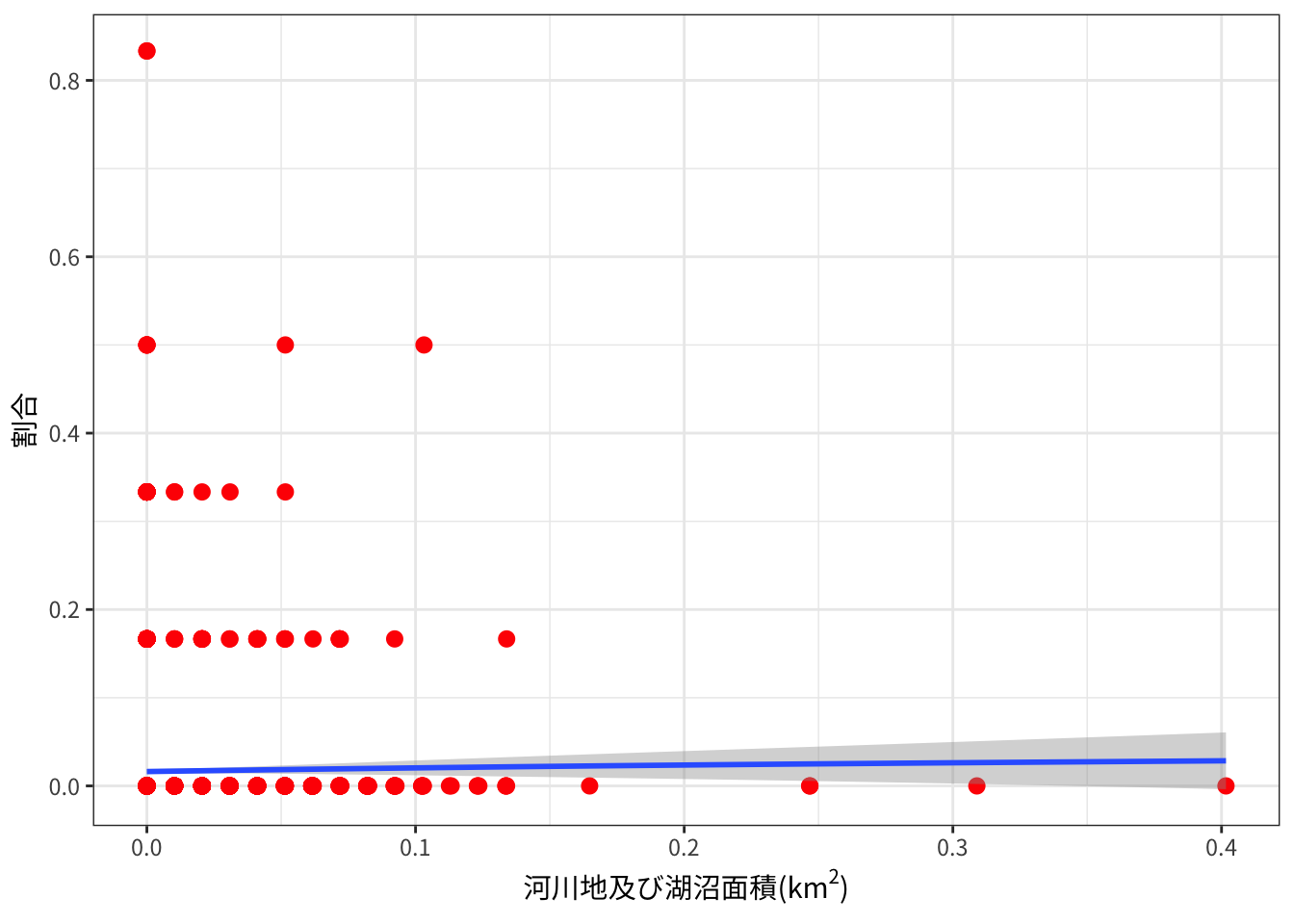
どこもあまり高くないようです。
ブナ豊凶との関係
ブナ豊凶とクマ出没件数との関係を見てみます。
そのための関数を定義します。
plot_buna_freq <- function(region, title = NULL,
xlab = "年", ylab = "出没件数") {
tidyr::expand_grid(
mesh_code = unique(landuse[[region]]$mesh_code),
year = 2019:2024
) |>
dplyr::left_join(kuma_sum, by = c("mesh_code", "year")) |>
tidyr::replace_na(list(present = 0, n = 0)) |>
dplyr::mutate(buna = if_else(year == 2020, "大凶作", "大凶作以外")) |>
ggplot(aes(x = as.factor(year), y = n, color = buna)) +
geom_jitter(size = 2.5, alpha = 0.5, height = 0, width = 0.05) +
labs(title = title, x = xlab, y = ylab) +
scale_color_discrete(name = "ブナの豊凶") +
theme_bw(base_family = "Noto Sans JP")
}加賀地方における加賀地方における、各年の3次メッシュごとのクマ出没件数です。大凶作の年(2020年)は赤色でしめしてあります。また見やすくするため、横軸方向にはランダムノイズを加えています。
plot_buna_freq("Kaga")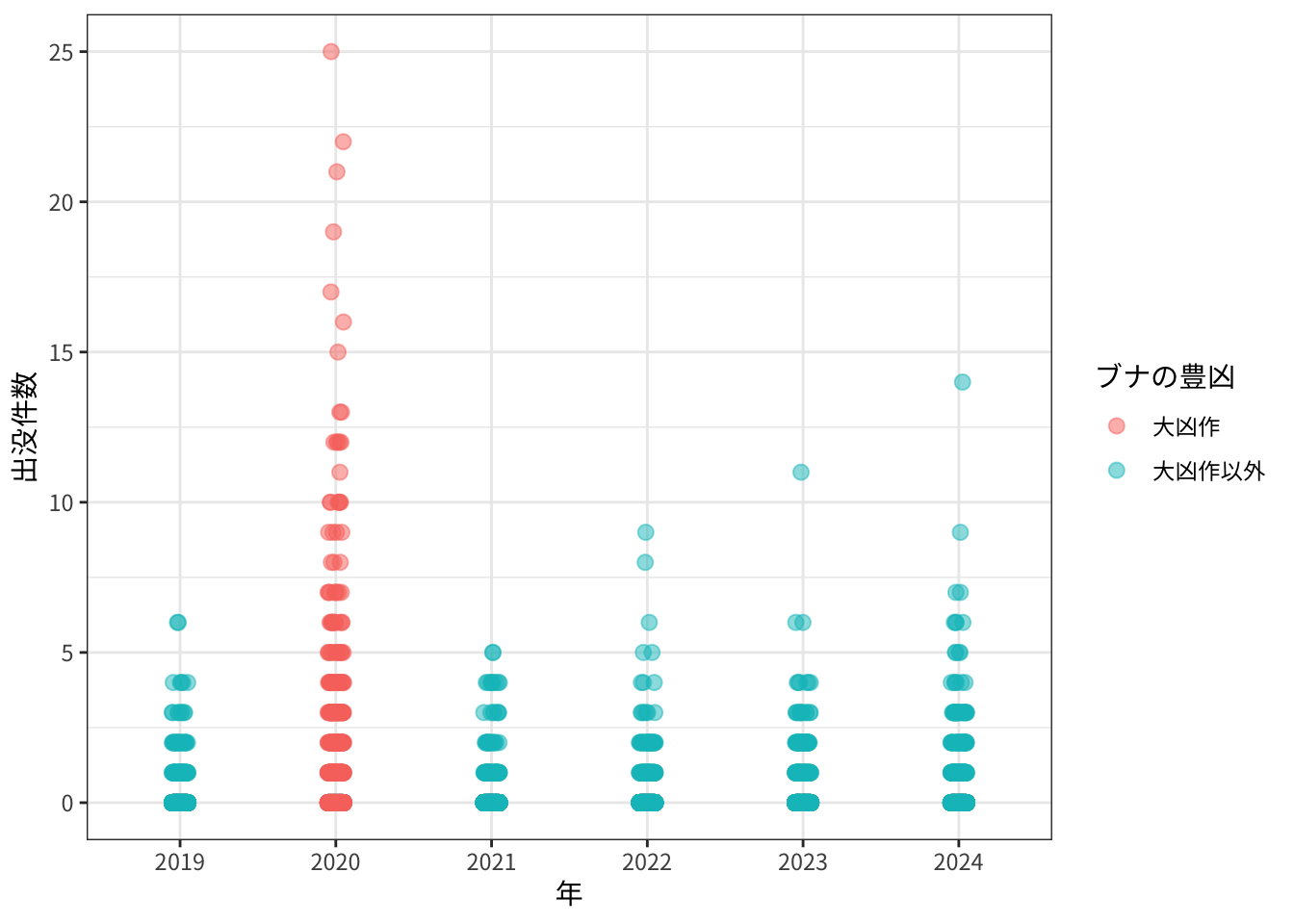
大凶作の2020年は出没件数がかなり多くなっています。
plot_buna_freq("Noto")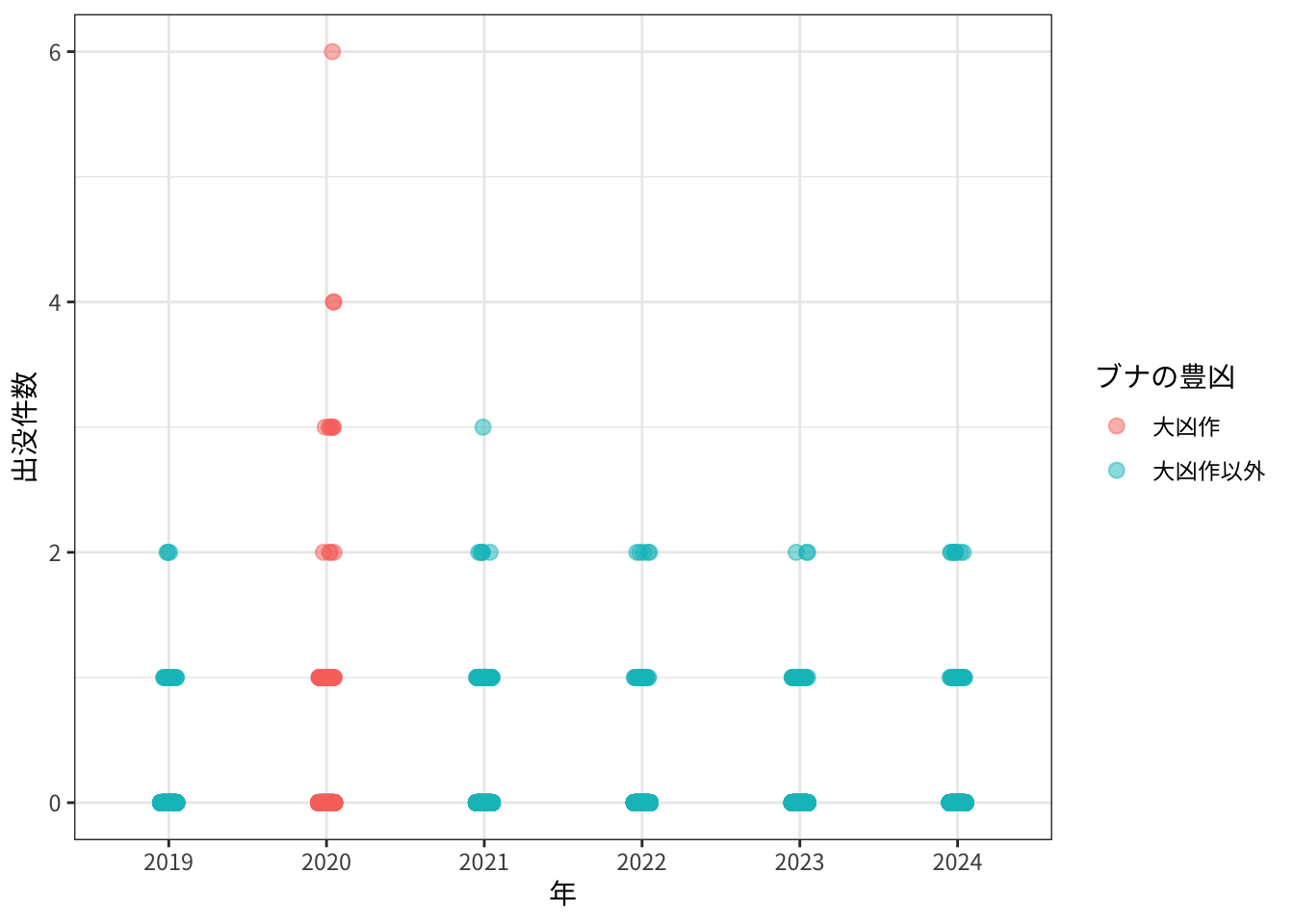
大凶作の2020年はやや多いようです。
クマ出没予測モデル
環境データの作成
モデルの説明変数として使用する可能性のある環境データを作成します。具体的には以下のような変数を作成します。
- forest: 3次メッシュ中の森林面積(km2)
- forest2: 3次メッシュ中の森林面積(km2)の2乗
- water: 3次メッシュ中の河川地及び湖沼面積(km2)
- water2: 3次メッシュ中の河川地及び湖沼面積(km2)の2乗
env_data <- purrr::map(
region, \(r) {
landuse[[r]] |>
dplyr::mutate(forest = `森林`,
forest2 = `森林`^2,
water = `河川地及び湖沼`,
water2 = `河川地及び湖沼`^2) |>
as.data.frame() |> # drop geometry
dplyr::select(mesh_code, forest, forest2, water, water2)
})
names(env_data) <- region3次メッシュコードと年のすべての組み合わせをつくっておき、これに出没のありなしデータと環境データを結合します。
kuma_env_data <- purrr::map(
region, \(r) {
tidyr::expand_grid(
mesh_code = unique(landuse[[r]]$mesh_code),
year = 2019:2024
) |>
dplyr::left_join(kuma_sum, by = c("mesh_code", "year")) |>
dplyr::mutate(present = replace_na(present, 0),
n = replace_na(n, 0)) |>
dplyr::left_join(env_data[[r]], by = "mesh_code") |>
# ブナ豊凶をしめすダミー変数`buna_poor`を追加(大凶作=1)
dplyr::mutate(buna_poor = if_else(year == 2020, 1, 0))
})
names(kuma_env_data) <- regionsdmTMBで使用するメッシュ作成のため、土地利用データにUTM座標系の座標を追加します。
coord <- purrr::map(
region, \(r) {
landuse[[r]] |>
sf::st_transform(4326) |> # WGS84
sf::st_make_valid() |>
sf::st_centroid() |>
sf::st_coordinates() |>
as.data.frame() |>
dplyr::rename(longitude = X, latitude = Y) |>
add_utm_columns(ll_names = c("longitude", "latitude"))
})
names(coord) <- regionUTM座標に3次メッシュコードを結合させます。
coord2 <- purrr::map(
region, \(r) {
coord[[r]] |>
bind_cols(
landuse[[r]] |>
dplyr::select(mesh_code)
)
})
names(coord2) <- region出没ありなし・環境データにUTM座標を結合させます。
kuma_env_coord <- purrr::map(
region, \(r) {
kuma_env_data[[r]] |>
dplyr::left_join(coord2[[r]], by = "mesh_code")
})
names(kuma_env_coord) <- regionsdmTMBの空間モデルのため、メッシュを作成します。
mesh <- purrr::map(
region, \(r) {
make_mesh(kuma_env_coord[[r]],
xy_cols = c("X", "Y"), cutoff = 2)
})
names(mesh) <- region作成されたメッシュの確認します。加賀地方です。
plot(mesh[["Kaga"]])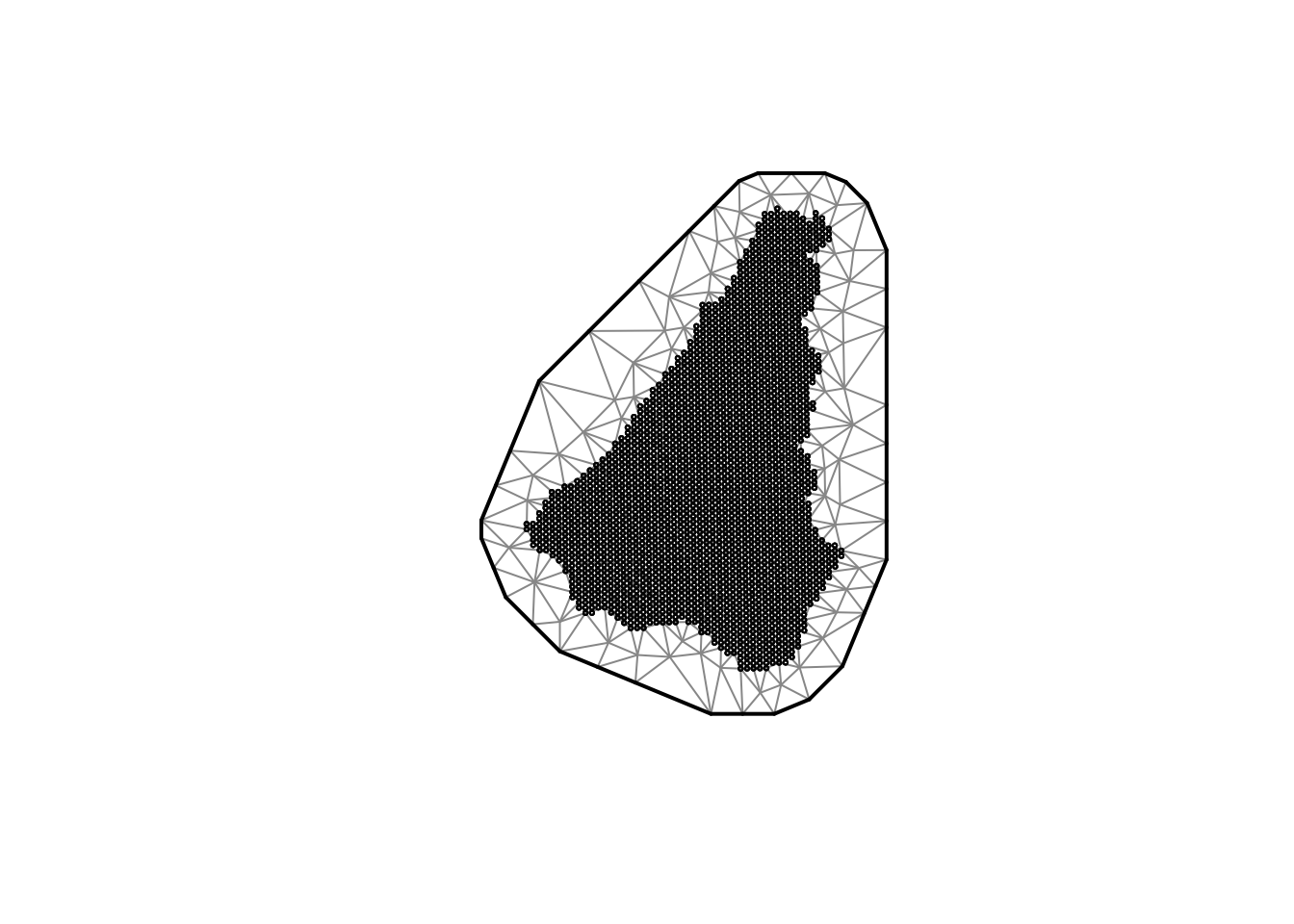
能登地方です。
plot(mesh[["Noto"]])
モデルの作成
説明変数を変えて以下の5つのモデルを作成しました。土地利用に関する説明変数は、背景知識から選択しました。
- モデル1: ブナの豊凶(
buna_poor)を説明変数とするモデル - モデル2: 森林面積(
forest)とその2乗を説明変数とするモデル - モデル3: 森林面積(
forest)とその2乗、ブナの豊凶(buna_poor)を説明変数とするモデル - モデル4: 森林面積(
forest)とその2乗、河川・湖沼面積(water)とその2乗を説明変数とするモデル - モデル5: 森林面積(
forest)とその2乗、河川・湖沼面積(water)とその2乗、ブナの豊凶(buna_poor)を説明変数とするモデル
formula <- vector("list", 5)
formula[[1]] <- as.formula("present ~ buna_poor")
formula[[2]] <- as.formula("present ~ forest + forest2")
formula[[3]] <- as.formula("present ~ forest + forest2 + buna_poor")
formula[[4]] <- as.formula("present ~ forest + forest2 + water + water2")
formula[[5]] <- as.formula("present ~ forest + forest2 + water + water2 + buna_poor")あてはめ
結果を格納するリストを作成します。
fit <- vector("list", 2)
names(fit) <- region加賀地方
まずは加賀地方からあてはめを実行します。
目的変数をクマ出没情報のありなし、説明変数はそれぞれ用意したもの、誤差構造は二項分布で、リンク関数はロジットとしています。また、時空間の自己相関をモデルに組み込むようにしています。
fit[["Kaga"]] <- purrr::map(
1:5, \(i) {
sdmTMB(formula[[i]],
data = kuma_env_coord[["Kaga"]],
mesh = mesh[["Kaga"]],
family = binomial(link = "logit"),
spatial = "on",
time = "year",
time_varying = ~ 1,
time_varying_type = "ar1",
extra_time = 2025)
})モデルのあてはめ結果をチェックします。
purrr::walk(1:5, \(i) {
cat(paste("model:", i, "\n"))
sdmTMB::sanity(fit[["Kaga"]][[i]])
})
## model: 1
## ✔ Non-linear minimizer suggests successful convergence
## ✔ Hessian matrix is positive definite
## ✔ No extreme or very small eigenvalues detected
## ✔ No gradients with respect to fixed effects are >= 0.001
## ✔ No fixed-effect standard errors are NA
## ✔ No standard errors look unreasonably large
## ✔ No sigma parameters are < 0.01
## ✔ No sigma parameters are > 100
## ✔ Range parameter doesn't look unreasonably large
## model: 2
## ✔ Non-linear minimizer suggests successful convergence
## ✔ Hessian matrix is positive definite
## ✔ No extreme or very small eigenvalues detected
## ✔ No gradients with respect to fixed effects are >= 0.001
## ✔ No fixed-effect standard errors are NA
## ✔ No standard errors look unreasonably large
## ✔ No sigma parameters are < 0.01
## ✔ No sigma parameters are > 100
## ✔ Range parameter doesn't look unreasonably large
## model: 3
## ✔ Non-linear minimizer suggests successful convergence
## ✔ Hessian matrix is positive definite
## ✔ No extreme or very small eigenvalues detected
## ✔ No gradients with respect to fixed effects are >= 0.001
## ✔ No fixed-effect standard errors are NA
## ✔ No standard errors look unreasonably large
## ✔ No sigma parameters are < 0.01
## ✔ No sigma parameters are > 100
## ✔ Range parameter doesn't look unreasonably large
## model: 4
## ✔ Non-linear minimizer suggests successful convergence
## ✔ Hessian matrix is positive definite
## ✔ No extreme or very small eigenvalues detected
## ✔ No gradients with respect to fixed effects are >= 0.001
## ✔ No fixed-effect standard errors are NA
## ✔ No standard errors look unreasonably large
## ✔ No sigma parameters are < 0.01
## ✔ No sigma parameters are > 100
## ✔ Range parameter doesn't look unreasonably large
## model: 5
## ✔ Non-linear minimizer suggests successful convergence
## ✔ Hessian matrix is positive definite
## ✔ No extreme or very small eigenvalues detected
## ✔ No gradients with respect to fixed effects are >= 0.001
## ✔ No fixed-effect standard errors are NA
## ✔ No standard errors look unreasonably large
## ✔ No sigma parameters are < 0.01
## ✔ No sigma parameters are > 100
## ✔ Range parameter doesn't look unreasonably largeいずれも問題は発見されませんでした。
AICを比較します。
purrr::walk(1:5, \(i) {
print(paste0("モデル", i, "のAIC: ", AIC(fit[["Kaga"]][[i]])))
})
## [1] "モデル1のAIC: 5302.83109360736"
## [1] "モデル2のAIC: 4948.74500061589"
## [1] "モデル3のAIC: 4946.29361973717"
## [1] "モデル4のAIC: 4938.24338079213"
## [1] "モデル5のAIC: 4935.79658029803"モデル5のAICがもっともちいさいという結果がえられました。予測能力が高いモデルとしてモデル5を採用します。
モデル5のあてはめ結果の要約を表示します。
summary(fit[["Kaga"]][[5]])
## Spatiotemporal model fit by ML ['sdmTMB']
## Formula: formula[[i]]
## Mesh: mesh[["Kaga"]] (isotropic covariance)
## Time column: year
## Data: kuma_env_coord[["Kaga"]]
## Family: binomial(link = 'logit')
##
## Conditional model:
## coef.est coef.se
## (Intercept) -5.85 0.80
## forest 9.49 0.72
## forest2 -9.83 0.60
## water 6.27 1.83
## water2 -15.68 4.50
## buna_poor 1.06 0.39
##
## Time-varying parameters:
## coef.est coef.se
## (Intercept)-2019 -0.0500000 0.2600000
## (Intercept)-2020 -0.0900000 0.2900000
## (Intercept)-2021 -0.1100000 0.2900000
## (Intercept)-2022 -0.0700000 0.3000000
## (Intercept)-2023 0.0900000 0.3000000
## (Intercept)-2024 0.2900000 0.3800000
## (Intercept)-2025 0.2000000 0.4000000
## rho-(Intercept) 0.6853522 0.6276213
##
## Matérn range: 13.67
## Spatial SD: 2.49
## Spatiotemporal IID SD: 0.83
## ML criterion at convergence: 2456.898
##
## See ?tidy.sdmTMB to extract these values as a data frame.能登地方
能登地方についても同じようにあてはめを実行します。
fit[["Noto"]] <- purrr::map(
1:5, \(i) {
sdmTMB(formula[[i]],
data = kuma_env_coord[["Noto"]],
mesh = mesh[["Noto"]],
family = binomial(link = "logit"),
spatial = "on",
time = "year",
time_varying = ~ 1,
time_varying_type = "ar1",
extra_time = 2025)
})モデルのあてはめ結果をチェックします。
purrr::walk(1:5, \(i) {
cat(paste("model:", i, "\n"))
sdmTMB::sanity(fit[["Noto"]][[i]])
})
## model: 1
## ✔ Non-linear minimizer suggests successful convergence
## ✔ Hessian matrix is positive definite
## ✔ No extreme or very small eigenvalues detected
## ✔ No gradients with respect to fixed effects are >= 0.001
## ✔ No fixed-effect standard errors are NA
## ✔ No standard errors look unreasonably large
## ✔ No sigma parameters are < 0.01
## ✔ No sigma parameters are > 100
## ✔ Range parameter doesn't look unreasonably large
## model: 2
## ✔ Non-linear minimizer suggests successful convergence
## ✔ Hessian matrix is positive definite
## ✔ No extreme or very small eigenvalues detected
## ✔ No gradients with respect to fixed effects are >= 0.001
## ✔ No fixed-effect standard errors are NA
## ✔ No standard errors look unreasonably large
## ✔ No sigma parameters are < 0.01
## ✔ No sigma parameters are > 100
## ✔ Range parameter doesn't look unreasonably large
## model: 3
## ✔ Non-linear minimizer suggests successful convergence
## ✔ Hessian matrix is positive definite
## ✔ No extreme or very small eigenvalues detected
## ✔ No gradients with respect to fixed effects are >= 0.001
## ✔ No fixed-effect standard errors are NA
## ✔ No standard errors look unreasonably large
## ✔ No sigma parameters are < 0.01
## ✔ No sigma parameters are > 100
## ✔ Range parameter doesn't look unreasonably large
## model: 4
## ✔ Non-linear minimizer suggests successful convergence
## ✔ Hessian matrix is positive definite
## ✔ No extreme or very small eigenvalues detected
## ✔ No gradients with respect to fixed effects are >= 0.001
## ✔ No fixed-effect standard errors are NA
## ✔ No standard errors look unreasonably large
## ✔ No sigma parameters are < 0.01
## ✔ No sigma parameters are > 100
## ✔ Range parameter doesn't look unreasonably large
## model: 5
## ✔ Non-linear minimizer suggests successful convergence
## ✔ Hessian matrix is positive definite
## ✔ No extreme or very small eigenvalues detected
## ✔ No gradients with respect to fixed effects are >= 0.001
## ✔ No fixed-effect standard errors are NA
## ✔ No standard errors look unreasonably large
## ✔ No sigma parameters are < 0.01
## ✔ No sigma parameters are > 100
## ✔ Range parameter doesn't look unreasonably largeいずれも問題は発見されませんでした。
AICを比較します。
purrr::walk(1:5, \(i) {
print(paste0("モデル", i, "のAIC: ", AIC(fit[["Noto"]][[i]])))
})
## [1] "モデル1のAIC: 1849.24235738959"
## [1] "モデル2のAIC: 1798.91126843042"
## [1] "モデル3のAIC: 1800.63098454961"
## [1] "モデル4のAIC: 1802.59181656214"
## [1] "モデル5のAIC: 1804.30948840935"モデル2のAICがもっともちいさいという結果がえられました。ただ、モデル3との差は少しですし、モデル作成者の判断としてブナの影響を含めたモデル3を予測モデルとして採用することにしました。
もっとも、能登にはブナの分布が少ないので、大凶作の影響も小さいのかもしれません。
モデル3のあてはめ結果の要約を表示します。
summary(fit[["Noto"]][[3]])
## Spatiotemporal model fit by ML ['sdmTMB']
## Formula: formula[[i]]
## Mesh: mesh[["Noto"]] (isotropic covariance)
## Time column: year
## Data: kuma_env_coord[["Noto"]]
## Family: binomial(link = 'logit')
##
## Conditional model:
## coef.est coef.se
## (Intercept) -6.80 0.59
## forest 7.19 1.03
## forest2 -6.38 0.92
## buna_poor 0.38 0.72
##
## Time-varying parameters:
## coef.est coef.se
## (Intercept)-2019 -0.35000000 0.4100000
## (Intercept)-2020 0.13000000 0.5800000
## (Intercept)-2021 0.85000000 0.5000000
## (Intercept)-2022 0.19000000 0.4500000
## (Intercept)-2023 -0.11000000 0.4100000
## (Intercept)-2024 0.06000000 0.3900000
## (Intercept)-2025 0.01000000 0.5200000
## rho-(Intercept) 0.08799818 0.5383671
##
## Matérn range: 15.94
## Spatial SD: 1.35
## Spatiotemporal IID SD: 1.05
## ML criterion at convergence: 891.315
##
## See ?tidy.sdmTMB to extract these values as a data frame.2025年の出没確率の予測
最後に、3次メッシュごとに、2025年のクマ出没確率を予測します。
予測に使用するリストを作成します。
newdata <- vector("list", 2)
names(newdata) <- region
pred <- vector("list", 2)
names(pred) <- region加賀地方
まずは、加賀地方です。
2025年はブナが大凶作と予測されているので、それを反映させて2025年のデータを作成します。
newdata[["Kaga"]] <- env_data[["Kaga"]] |>
dplyr::left_join(coord2[["Kaga"]], by = "mesh_code") |>
dplyr::mutate(buna_poor = 1,
year = 2025)モデル5を使用して2025年の出没確率を予測します。
【2025-09-12】予測分布の上側20%点を予測値として使用するようにしました。
est <- predict(fit[["Kaga"]][[5]], newdata[["Kaga"]],
type = "response", nsim = 2000)
upper <- apply(est, 1, quantile, 0.8) # 上側20%点
pred[["Kaga"]] <- newdata[["Kaga"]] |>
dplyr::mutate(pred = upper) |>
dplyr::select(mesh_code, pred, geometry)出没確率を地図化します。pred[["Kaga"]]は通常のデータフレームになっていますので、sf::st_as_sf()でsf型に変換します。
pred[["Kaga"]] |>
sf::st_as_sf() |>
ggplot(aes(fill = pred)) +
geom_sf() +
scale_fill_viridis_c(name = "出没確率", limits = c(0, 1)) +
theme_minimal(base_family = "Noto Sans JP")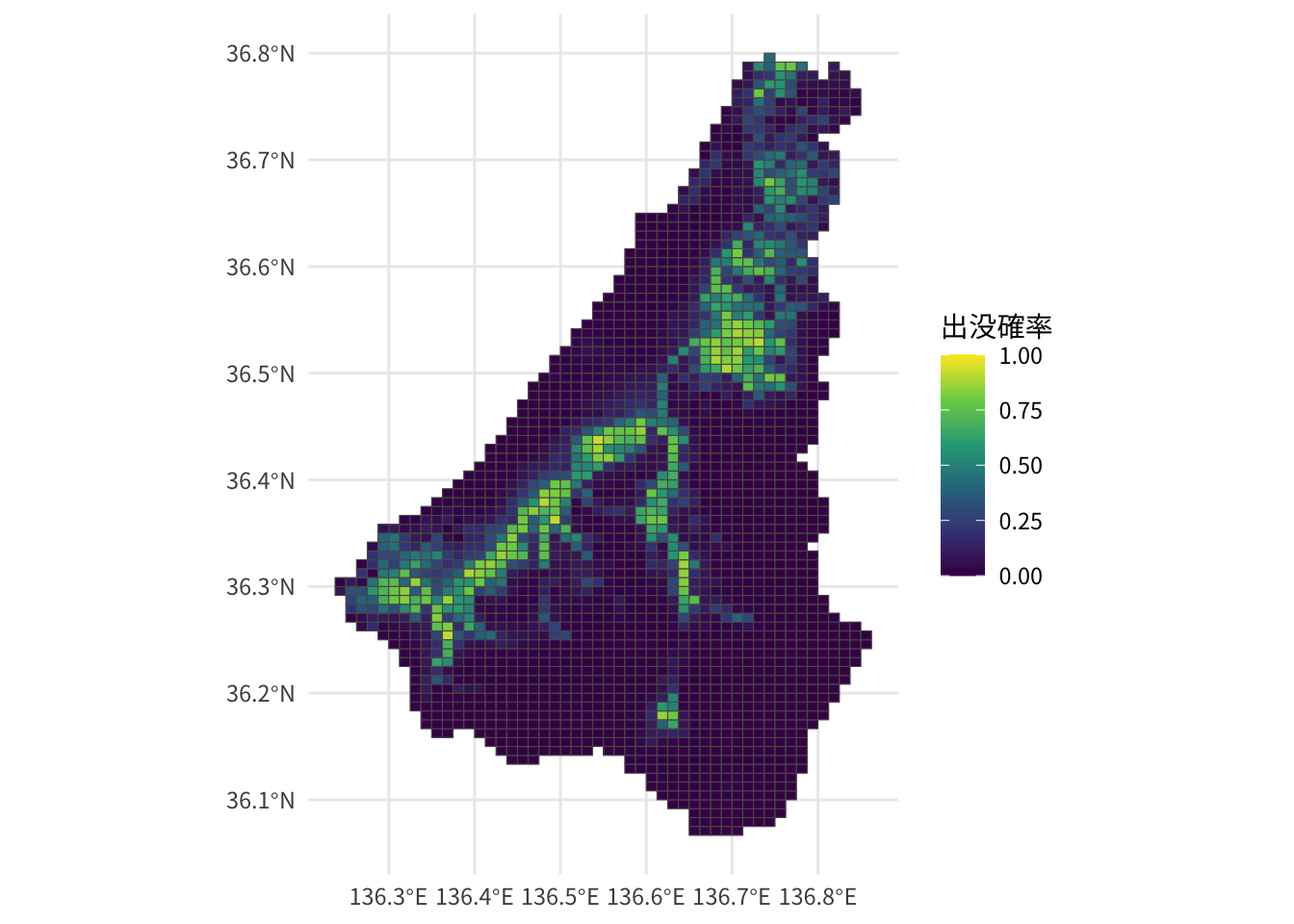
能登地方
つづいて能登地方です。
能登地方については、ブナ豊凶は予測モデルには含まれませんが、いちおう大凶作として2025年のデータを作成します。
newdata[["Noto"]] <- env_data[["Noto"]] |>
dplyr::left_join(coord2[["Noto"]], by = "mesh_code") |>
dplyr::mutate(buna_poor = 1,
year = 2025)ブナ大凶作かどうかを含めたモデル3を使用して2025年の出没確率を予測します。
【2025-09-12】予測分布の上側20%点を予測値として使用するようにしました。
est <- predict(fit[["Noto"]][[3]], newdata[["Noto"]],
type = "response", nsim = 2000)
upper <- apply(est, 1, quantile, 0.8) # 上側20%点
pred[["Noto"]] <- newdata[["Noto"]] |>
dplyr::mutate(pred = upper) |>
dplyr::select(mesh_code, pred, geometry)出没確率を地図化します。
pred[["Noto"]] |>
sf::st_as_sf() |>
ggplot(aes(fill = pred)) +
geom_sf() +
scale_fill_viridis_c(name = "出没確率", limits = c(0, 1)) +
theme_minimal(base_family = "Noto Sans JP")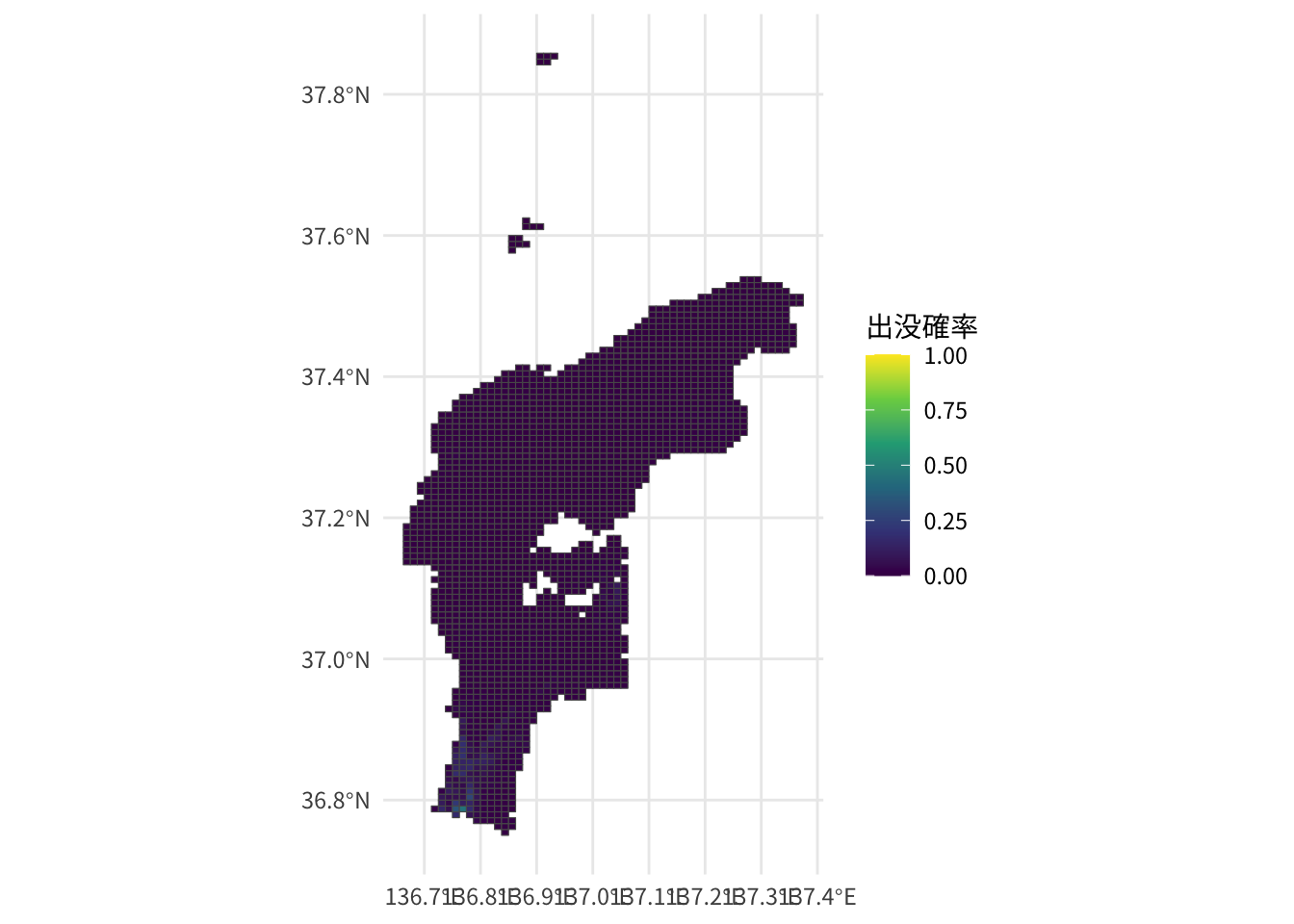
能登地方では、加賀地方との境界付近をのぞいて出没確率が低く予測されました。これは、3次メッシュ単位で年ごとの出没情報のありなしを目的変数にして、空間自己相関をガウスランダム場としているため、出没情報が粗な能登地方では全般に予測確率が低くなるのではないかと考えられます。
予測データの統合
加賀地方と能登地方の予測データを結合させて、両者で重複しているメッシュを抽出します。
pred_all <- bind_rows(pred)
dup <- pred_all |>
dplyr::count(mesh_code) |>
dplyr::filter(n > 1)重複しているメッシュでは予測値は両者の平均とします。
pred_dup <- pred_all |>
dplyr::filter(mesh_code %in% dup$mesh_code) |>
dplyr::group_by(mesh_code) |>
dplyr::summarise(pred = mean(pred), .groups = "drop")重複メッシュの予測値を更新し、重複を除いて、必要な変数だけを抽出します。
combinded_pred <- pred_all |>
dplyr::left_join(pred_dup, by = "mesh_code") |>
dplyr::mutate(pred = if_else(is.na(pred.y), pred.x, pred.y)) |>
dplyr::distinct(mesh_code, .keep_all = TRUE) |>
dplyr::select(mesh_code, pred, geometry) |>
sf::st_as_sf()ggplot(combinded_pred, aes(fill = pred)) +
geom_sf() +
scale_fill_viridis_c(name = "出没確率", limits = c(0, 1)) +
theme_minimal(base_family = "Noto Sans JP")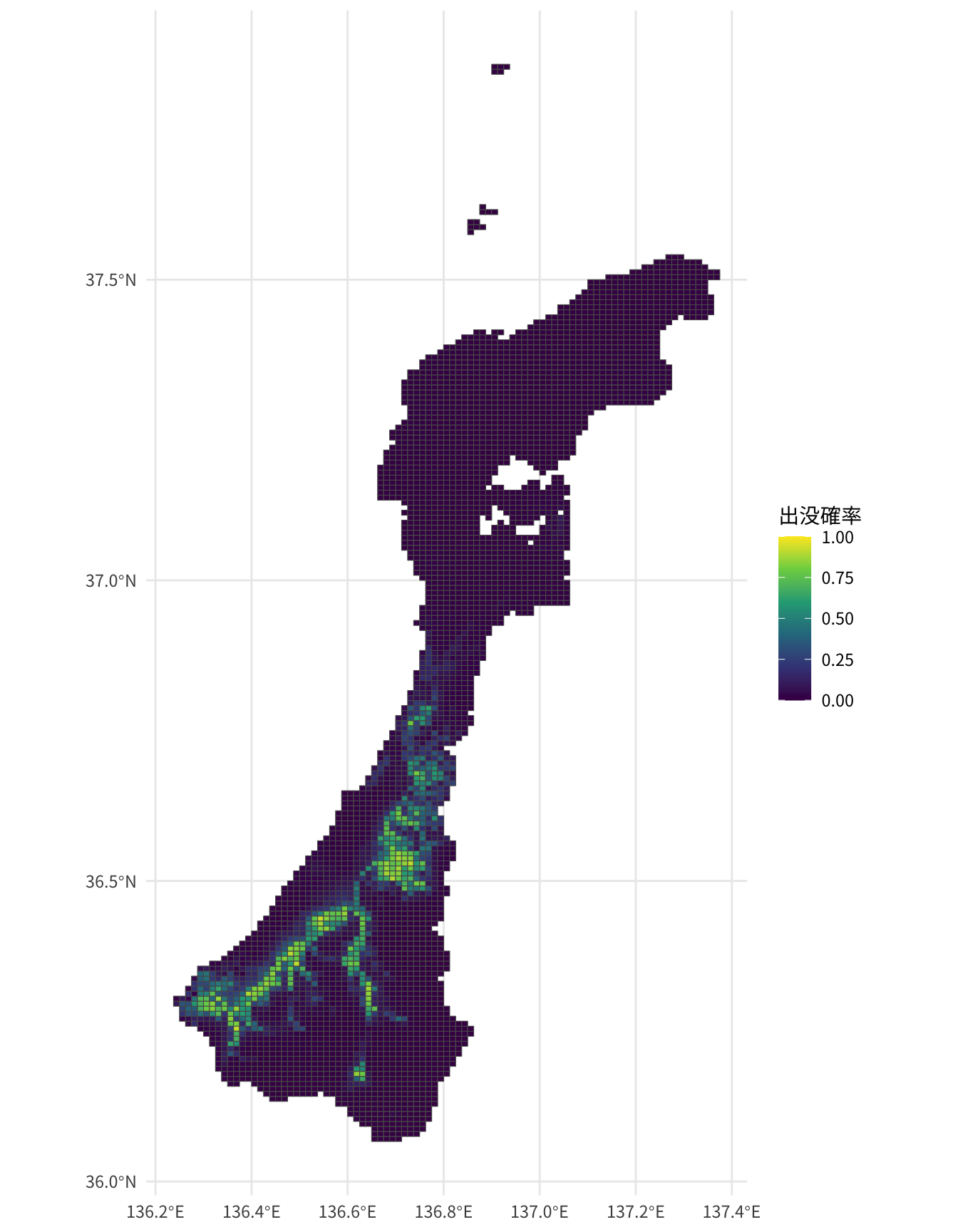
ファイルに出力しておきます。
output_file <- file.path("outputs", "kuma_prediction.geojson")
if (file.exists(output_file))
file.remove(output_file)
## [1] TRUE
sf::st_write(combinded_pred, output_file)
## Writing layer `kuma_prediction' to data source
## `outputs/kuma_prediction.geojson' using driver `GeoJSON'
## Writing 4512 features with 2 fields and geometry type Polygon.2025年の出没予測確率と実際の出没データの比較
2025年の出没状況を読み込みます。
occ_2025 <- file.path(data_dir, "bear_sightings_r7.csv") |>
readr::read_csv() |>
dplyr::mutate(mesh_code = jpmesh::coords_to_mesh(`経度`, `緯度`, 1) |>
as.character()) |>
dplyr::group_by(mesh_code) |>
dplyr::summarise(n = n(), .groups = "drop")
## Rows: 103 Columns: 11
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## chr (8): WKT, 出没日, 時間, 市町名, 場所, 備考, 頭数, 月
## dbl (2): 緯度, 経度
## lgl (1): 番号
##
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.予測と、実際の2025年の出没データを結合します。
bind_2025 <- combinded_pred |>
dplyr::left_join(occ_2025, by = "mesh_code") |>
dplyr::mutate(occ_2025 = if_else(is.na(n), 0, 1))予測確率を区分して、各区分ごとの出没ありの割合を計算し、グラフにします。
breaks <- seq(0, 1, 0.2)
n_breaks <- length(breaks)
prop_2025 <- bind_2025 |>
dplyr::mutate(pred_cat = cut(pred, breaks,
include.lowest = TRUE)) |>
dplyr::group_by(pred_cat) |>
dplyr::summarise(n = n(),
n_present = sum(occ_2025),
prop_present = n_present / n,
.groups = "drop") |>
dplyr::mutate(mid = (breaks[2:n_breaks] +
breaks[1:(n_breaks - 1)]) / 2)
ggplot(prop_2025, aes(x = mid, y = prop_present)) +
geom_col(fill = "red", alpha = 0.7) +
scale_x_continuous(limits = c(min(breaks), max(breaks)),
breaks = breaks, minor_breaks = NULL) +
scale_y_continuous(limits = c(0, 1),
breaks = breaks) +
labs(x = "2025年の出没予測確率区分",
y = "出没ありの割合") +
theme_bw(base_family = "Noto Sans JP")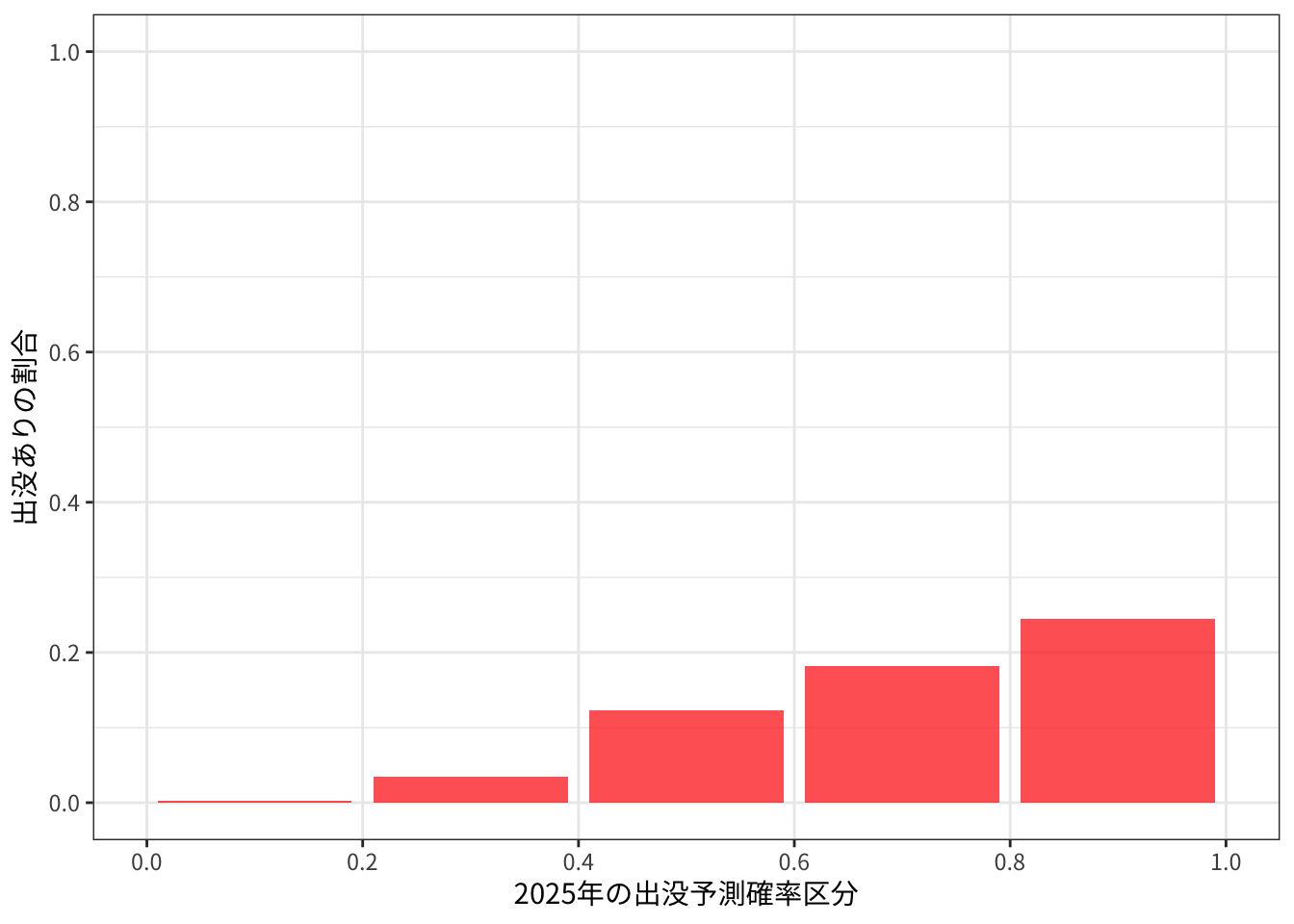
ことしの出現情報はまだこれから増えるところですので、縦軸はこれから高くなっていくと考えられます。右に行くほど割合が高くなっているというところは、現在のところはうまく推定できているようです。
おわりに
石川県全体の2025年のクマ出没確率予測マップが完成しました。これをGISで使用したり、ウェブアプリで表示したりといった利用が考えられます。
なお、出没確率が低く予測されていても、クマが出没しないとは言い切れません。クマが生息していそうな場所に立ち入るときは鈴を持参するとか、誘引物を放置しないとかいった基本的な対策が必要です。