変量効果を適切に使う必要がある例

R
作者

伊東宏樹

公開

2025年9月12日

データ中に構造があるときには、変量効果（ランダム効果）を含めた混合効果モデルで適切にモデリングする必要があるとよくいわれるのですが、その例をつくってみました。いくつかの群からサンプリングをおこなっており、データ中にクラスタがある（擬似反復がある）場合を想定しています。

準備

ggplot2パッケージと、混合効果モデル用にlmerTestパッケージを読み込みます。また、擬似乱数のシードを設定します。

library(ggplot2)
library(lmerTest)
## Loading required package: lme4
## Loading required package: Matrix
## 
## Attaching package: 'lmerTest'
## The following object is masked from 'package:lme4':
## 
##     lmer
## The following object is masked from 'package:stats':
## 
##     step

set.seed(1234)

データ

まずは1例です。模擬データを生成します。

群の数、各群内のデータ数を設定します。

n_group <- 10
n_samp <- 5

n_group個の群をつくります。

group <- factor(letters[1:n_group])

標準偏差を設定します。

  • sigma1: 残差標準偏差
  • sigma2: 変量効果の標準偏差
  • sigma3: 群内の説明変数の標準偏差
sigma1 <- 1
sigma2 <- 1
sigma3 <- 0.5

説明変数を生成します。

x0 <- rnorm(n_group, 5, 2.5)
x <- rnorm(n_group * n_samp, rep(x0, each = n_samp), sigma3)

変量効果を生成します。

ranef <- rnorm(n_group, 0, sigma2) |>
  rep(each = n_samp)

目的変数を生成します。説明変数とは無関係で、切片と変量効果と誤差からなるという設定です。

y <- 1 + ranef + rnorm(n_group * n_samp, 0, sigma1)

データフレームにまとめます。

df <- data.frame(x = x, y = y,
                 group = rep(group, each = n_samp))

群ごとに色を変えてプロットします。

ggplot(df, aes(x = x, y = y, color = group)) +
  geom_point(size = 3)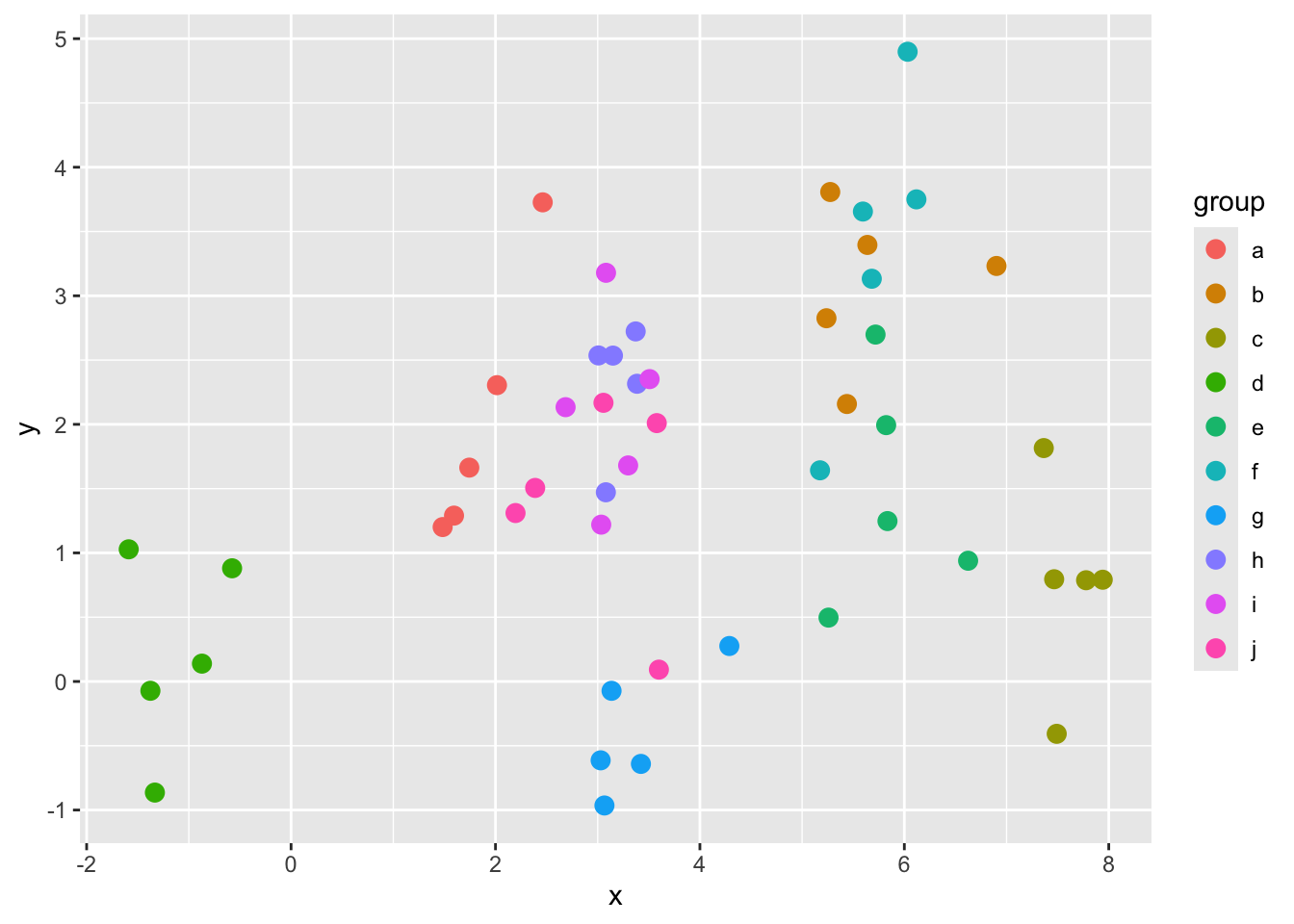

あてはめ

線形回帰

まずは、群を無視して線形回帰モデルにあてはめます。

lm(y ~ x, data = df) |>
  summary()
## 
## Call:
## lm(formula = y ~ x, data = df)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.67450 -1.09290  0.06688  0.96290  2.87916 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)   
## (Intercept)  0.99181    0.35090   2.827  0.00684 **
## x            0.17029    0.07769   2.192  0.03327 * 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.319 on 48 degrees of freedom
## Multiple R-squared:  0.09098,    Adjusted R-squared:  0.07204 
## F-statistic: 4.804 on 1 and 48 DF,  p-value: 0.03327

説明変数の係数は有意に0と異なるという結果になりました。ただし、真値は0です。

線形混合モデル

群を変量効果に設定した線形混合モデルにあてはめます。

lmer(y ~ x + (1|group), data = df) |>
  summary()
## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: y ~ x + (1 | group)
##    Data: df
## 
## REML criterion at convergence: 143
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -1.93817 -0.53114 -0.02397  0.51082  2.04950 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  group    (Intercept) 1.3387   1.1570  
##  Residual             0.6215   0.7884  
## Number of obs: 50, groups:  group, 10
## 
## Fixed effects:
##             Estimate Std. Error      df t value Pr(>|t|)  
## (Intercept)   0.7007     0.6558 11.6065   1.068   0.3071  
## x             0.2464     0.1392 14.3176   1.769   0.0981 .
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##   (Intr)
## x -0.812

こちらは説明変数は有意にはなりませんでした。

シミュレーション

1回だけではよくわかりませんので、繰り返しシミュレーションで、算出されるp値の分布をみてみます。

シミュレーション用の関数を定義します。

sim_func <- function(n_group = 10,
                     n_samp = 5,
                     sigma1 = 1,
                     sigma2 = 1,
                     sigma3 = 0.5) {
  # 説明変数
  x0 <- runif(n_group, 0, 10)
  x <- rnorm(n_group * n_samp, rep(x0, each = n_samp), sigma3)
  
  # 変量効果
  ranef <- rnorm(n_group, 0, sigma2) |>
    rep(each = n_samp)

  # 目的変数
  y <- 1 + ranef + rnorm(n_group * n_samp, 0, sigma1)
  
  # データフレームにまとめる
  df <- data.frame(x = x, y = y,
                   group = factor(rep(1:n_group, each = n_samp)))

  # 線形回帰
  fit_lm <- lm(y ~ x, data = df)
  
  # 線形混合モデル
  fit_lme <- lmer(y ~ x + (1|group), data = df)

  # p値を返す
  c(summary(fit_lm)$coefficients["x", "Pr(>|t|)"],
    summary(fit_lme)$coefficients["x", "Pr(>|t|)"])
}

設定1

関数のデフォルトの、n_group = 10, n_samp = 5, sigma1 = 1, sigma2 = 1, sigma3 = 0.5 という設定で1000回繰り返します。

R <- 1000
sim <- replicate(R, sim_func())

結果をヒストグラムにします。

data.frame(p_value = c(sim[1, ], sim[2, ]),
           method = rep(c("lm", "lme"), each = R)) |>
  ggplot(aes(x = p_value)) +
  geom_histogram(breaks = seq(0, 1, 0.05)) +
  facet_wrap(~method, ncol = 2)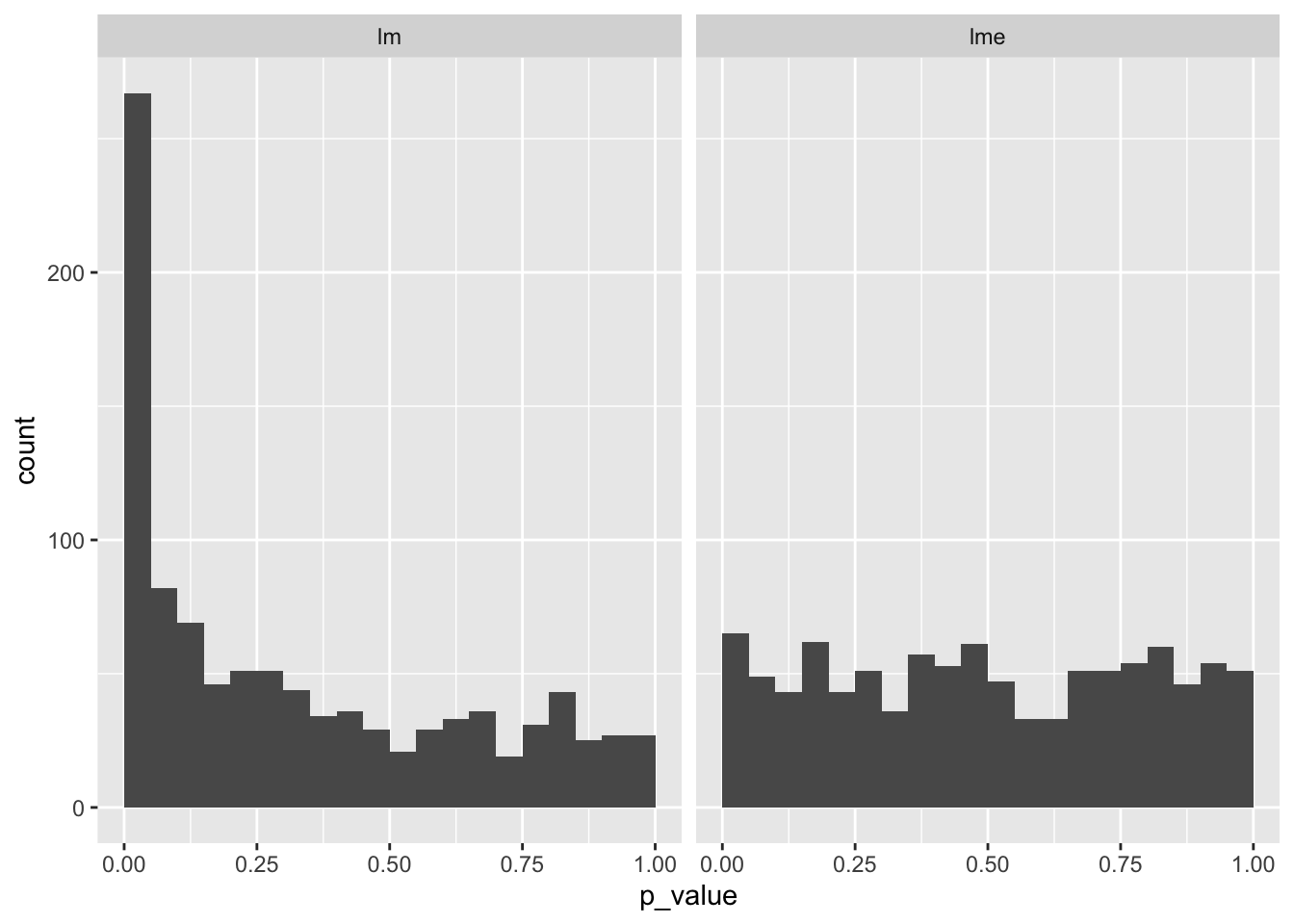

通常の線形回帰(lm)ではp<0.05となったものが、あきらかに全体の5%（縦軸の50）よりも多くありました。

設定2

群の数を大きくしてみました(n_group = 100)。

sim2 <- replicate(R, sim_func(n_group = 100))
data.frame(p_value = c(sim2[1, ], sim2[2, ]),
           method = rep(c("lm", "lme"), each = R)) |>
  ggplot(aes(x = p_value)) +
  geom_histogram(breaks = seq(0, 1, 0.05)) +
  facet_wrap(~method, ncol = 2)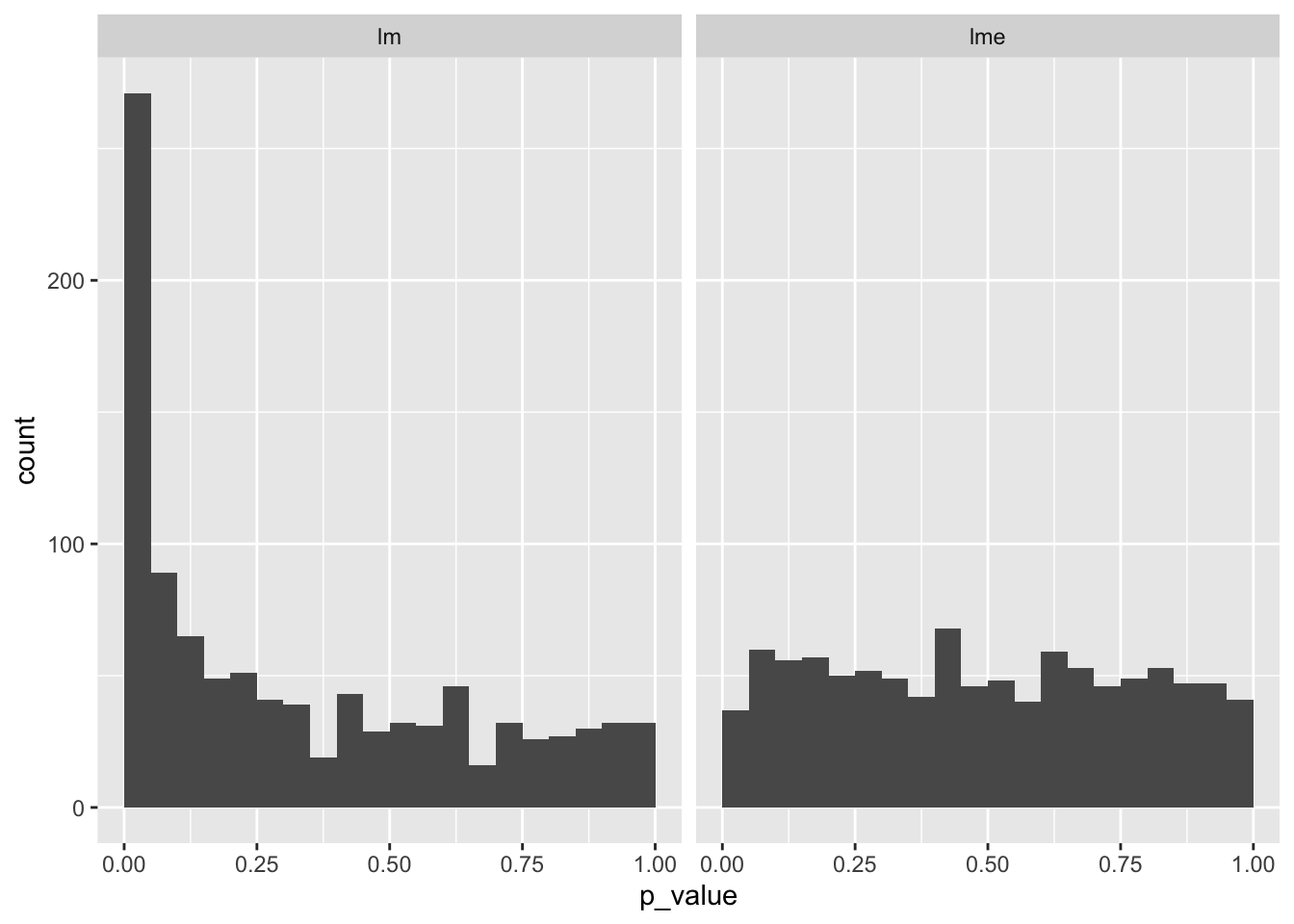

やはり通常の線形回帰(lm)ではp<0.05となったものが5%より多いという結果になりました。

設定3

次に、群内のデータ数を少なくしてみました(n_group = 100, n_samp = 2)。

sim3 <- replicate(R, sim_func(n_group = 100, n_samp = 2))
data.frame(p_value = c(sim3[1, ], sim3[2, ]),
           method = rep(c("lm", "lme"), each = R)) |>
  ggplot(aes(x = p_value)) +
  geom_histogram(breaks = seq(0, 1, 0.05)) +
  facet_wrap(~method, ncol = 2)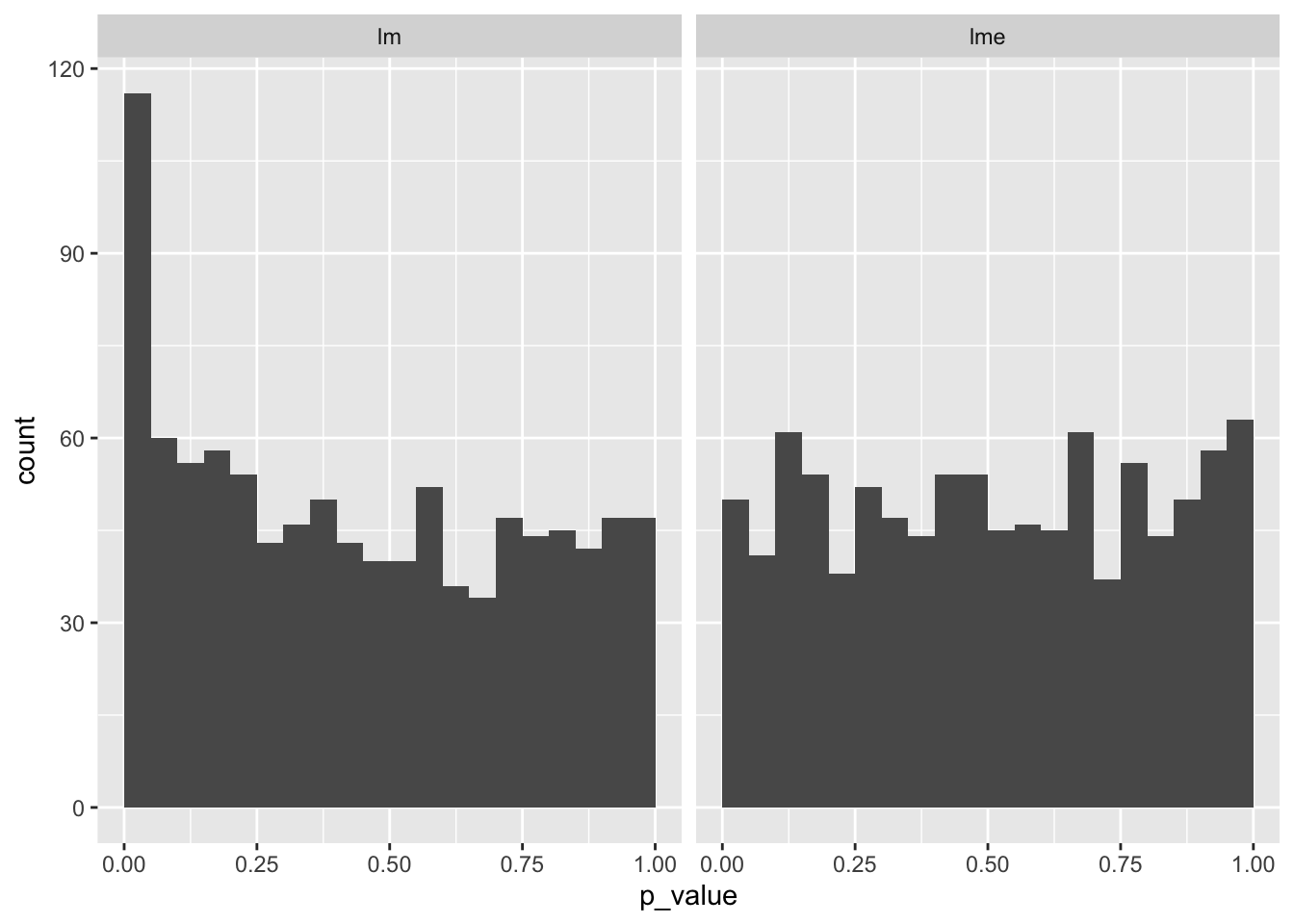

だいぶマシになりましたが、やはりp<0.05が5％より多いようです。

結論

ということで、変量効果を適切につかわないといけません。