library(gamlss)
## Loading required package: splines
## Loading required package: gamlss.data
##
## Attaching package: 'gamlss.data'
## The following object is masked from 'package:datasets':
##
## sleep
## Loading required package: gamlss.dist
## Loading required package: nlme
## Loading required package: parallel
## ********** GAMLSS Version 5.5-0 **********
## For more on GAMLSS look at https://www.gamlss.com/
## Type gamlssNews() to see new features/changes/bug fixes.
library(ggplot2)R研究集会2025での安川武彦さんの発表「Rでできる分布回帰のいろいろ」で、GAMLSS (Generalized Additive Models for Location Scale and Shape)とRの[gamlss[(https://cran.r-project.org/package=gamlss)パッケージのことを知りました。期待値だけではなく、分散や歪度、尖度などもモデル化して、あてはめるというものです。さっそく試してみました。
準備
gamlssパッケージと、グラフ作成のためにggplot2パッケージを読み込みます。
データ
gamlssパッケージに含まれるabdomデータを使います。妊娠週数(x)と胎児の腹囲(y, mm)のデータです。
data(abdom)
head(abdom)
## y x
## 1 59 12.29
## 2 64 12.29
## 3 56 12.29
## 4 61 12.43
## 5 74 12.71
## 6 60 12.71まずはデータをプロットしてみます。
ggplot(abdom, aes(x = x, y = y)) +
geom_point() +
labs(x = "Gestational age (weeks)",
y = "Abdominal circumference (mm)")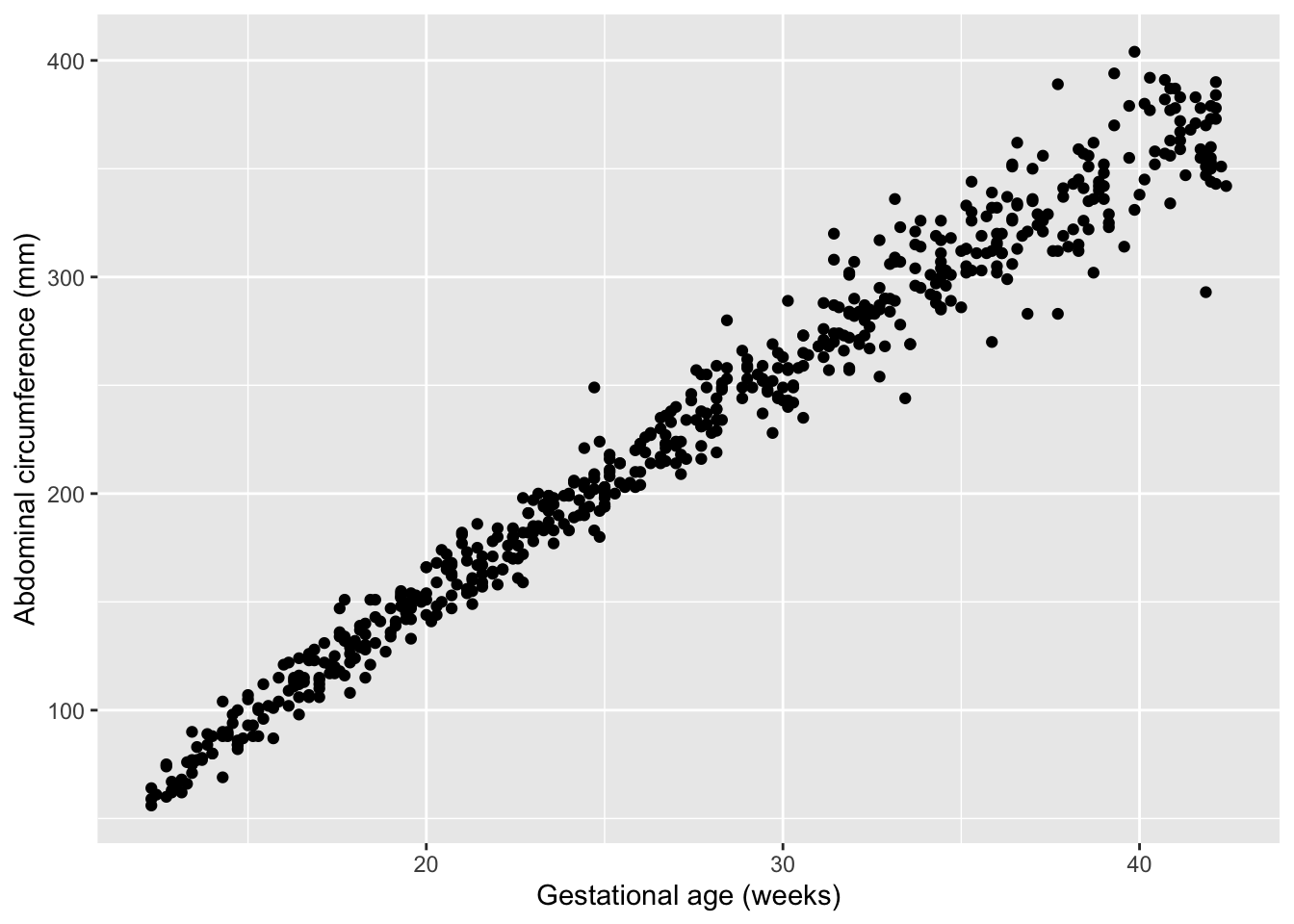
xがおおきくなるにつれて、yのばらつきもおおきくなっているようです。
モデルあてはめ
線形モデル
まずは通常の線形モデルをあてはめてみます。
fit_lm <- lm(y ~ x, data = abdom)
summary(fit_lm)
##
## Call:
## lm(formula = y ~ x, data = abdom)
##
## Residuals:
## Min 1Q Median 3Q Max
## -84.579 -8.105 -0.185 8.064 54.325
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -55.1795 2.0010 -27.58 <2e-16 ***
## x 10.3382 0.0701 147.49 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 14.63 on 608 degrees of freedom
## Multiple R-squared: 0.9728, Adjusted R-squared: 0.9728
## F-statistic: 2.175e+04 on 1 and 608 DF, p-value: < 2.2e-16AICの値も見てみます。
AIC(fit_lm)
## [1] 5008.453診断プロットを作成します。これは線形回帰モデルの診断でも紹介したものです。上から、残差プロット、正規Q-Qプロット、標準化残差の絶対値の平方根プロット、てこ比と標準化残差との関係とCookの距離を示したプロットになります。
plot(fit_lm, ask = FALSE)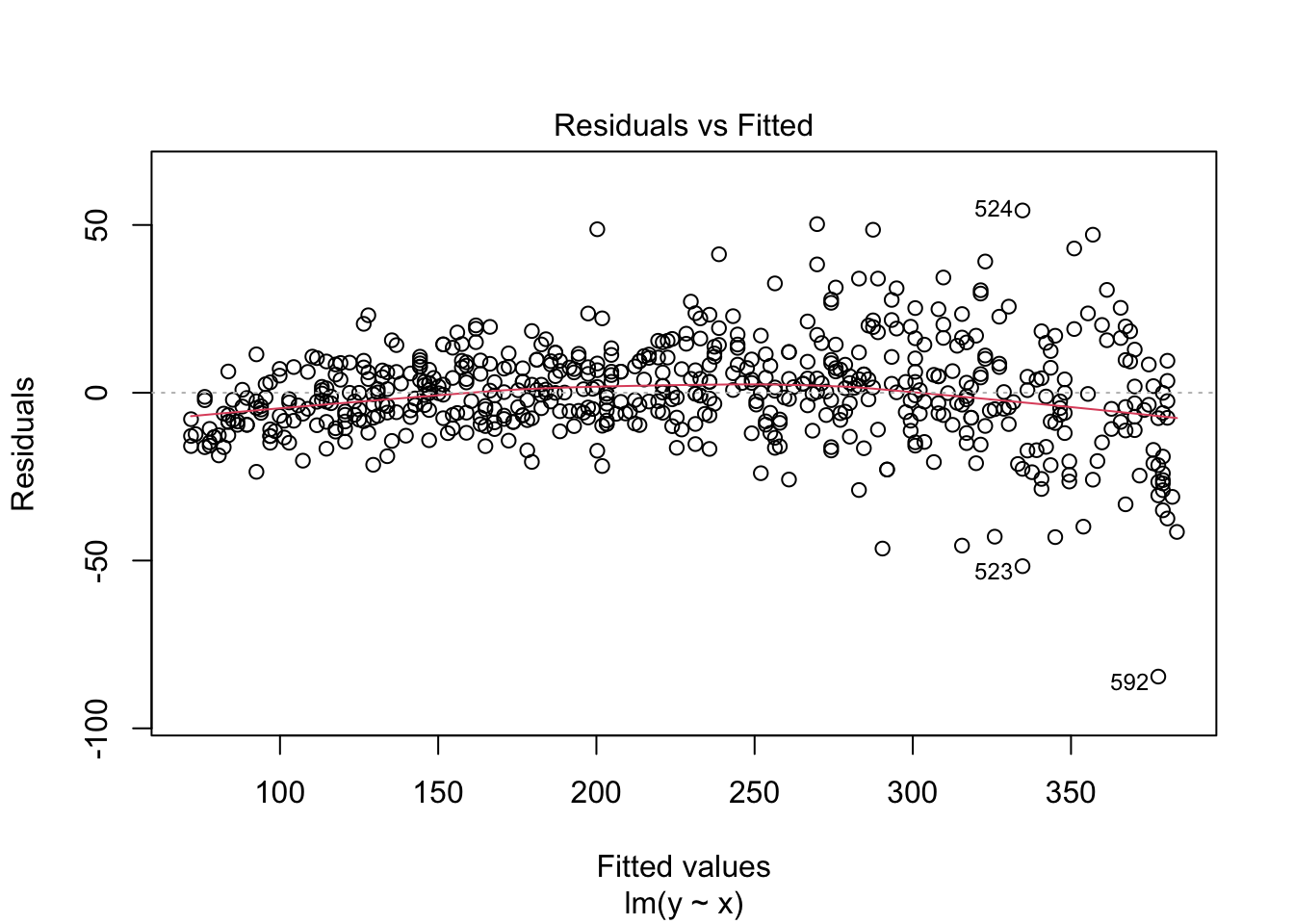
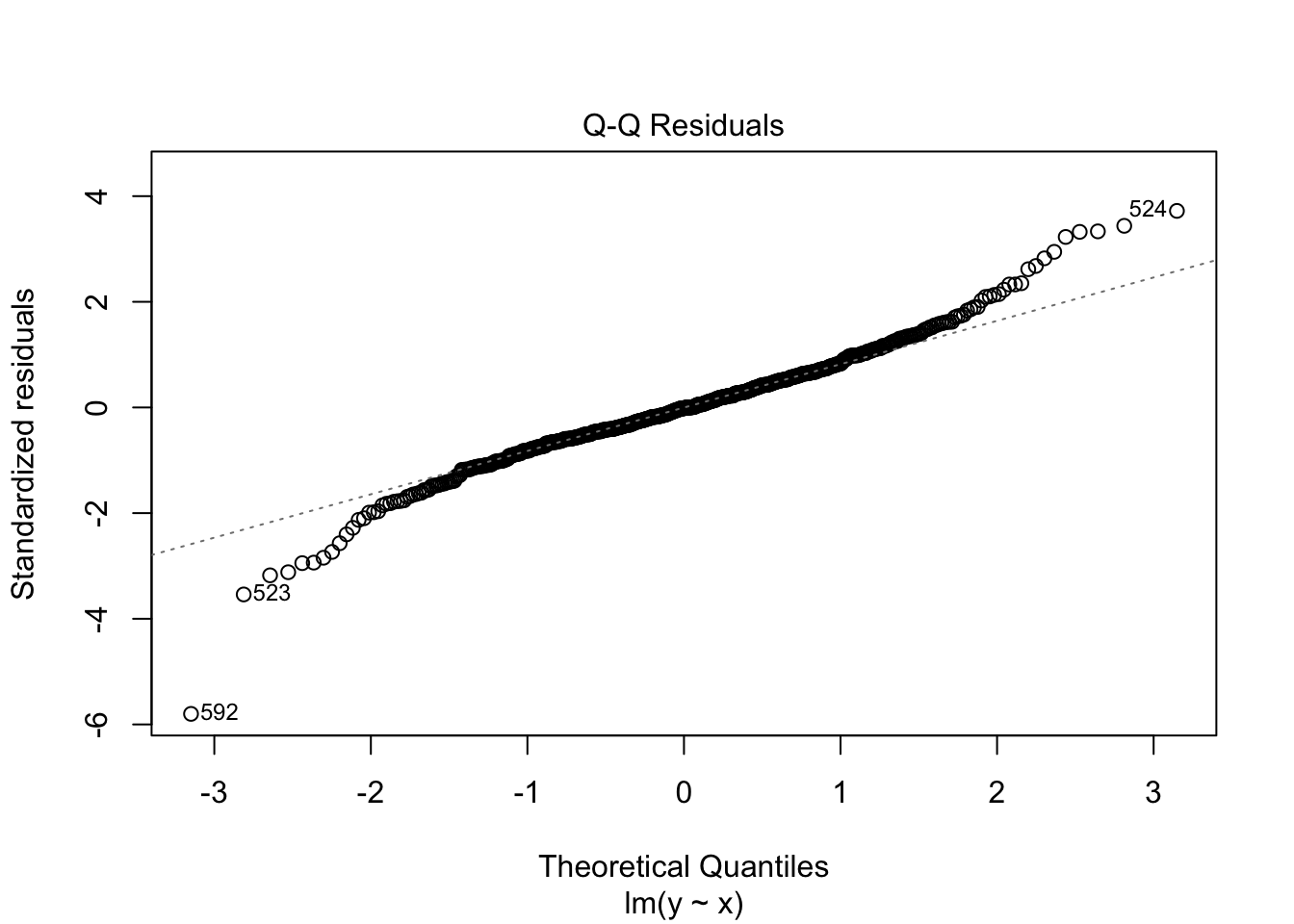
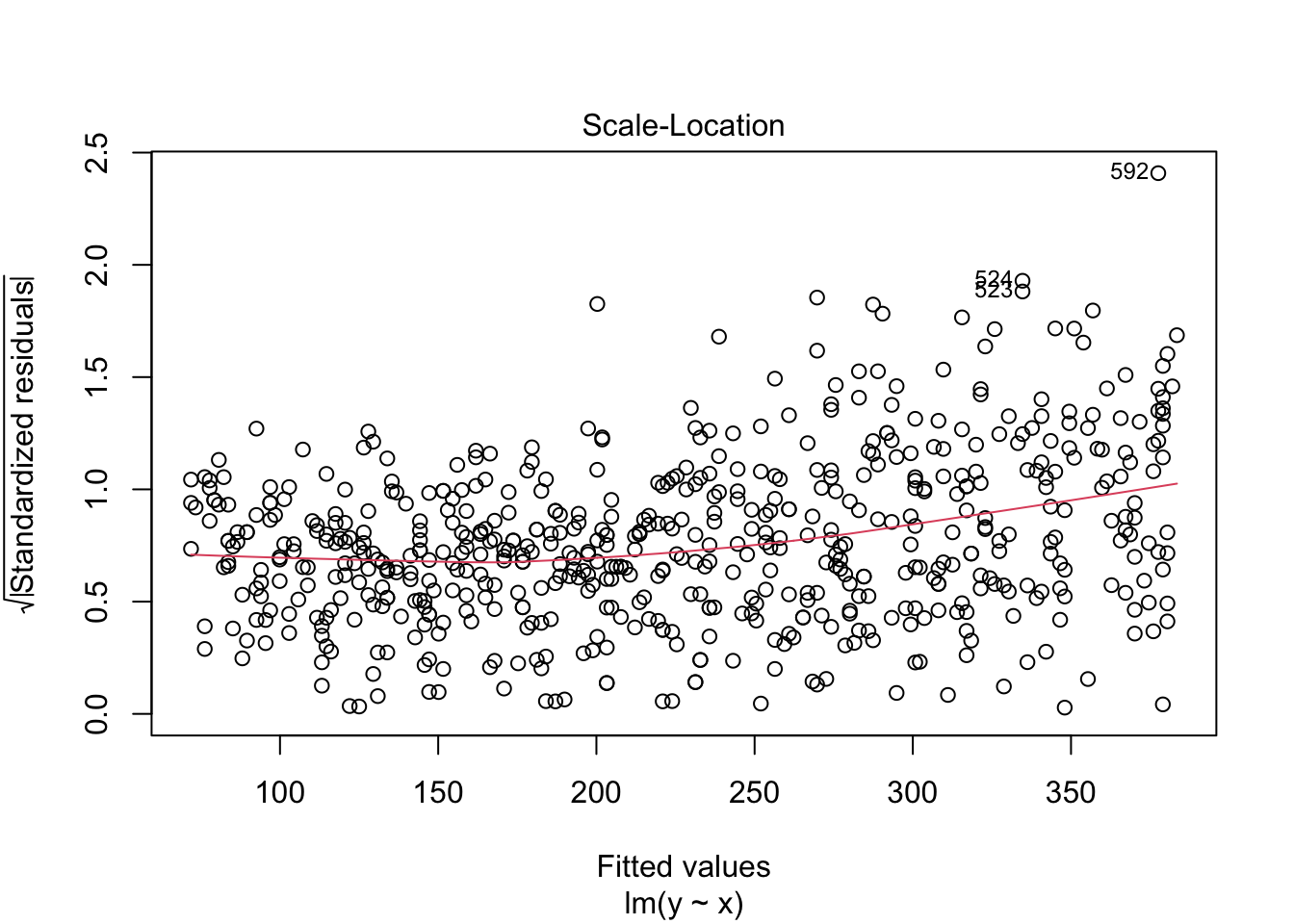
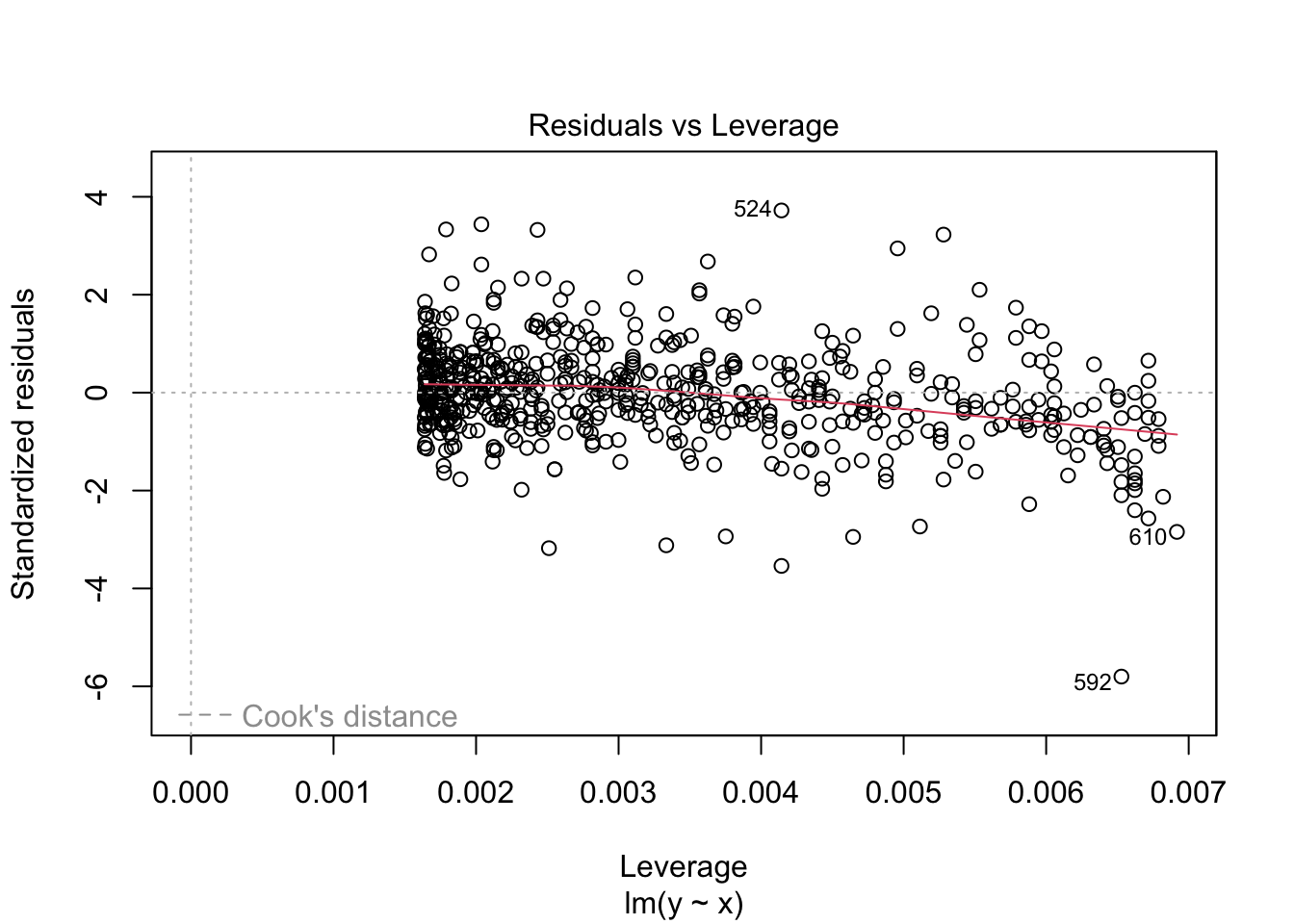
ggplot2でも、残差プロットと正規Q-Qプロットを作成してみます。
ggplot(abdom, aes(x = fitted(fit_lm), y = resid(fit_lm))) +
geom_point() +
geom_hline(yintercept = 0, linetype = "dashed") +
labs(x = "Fitted values",
y = "Residuals")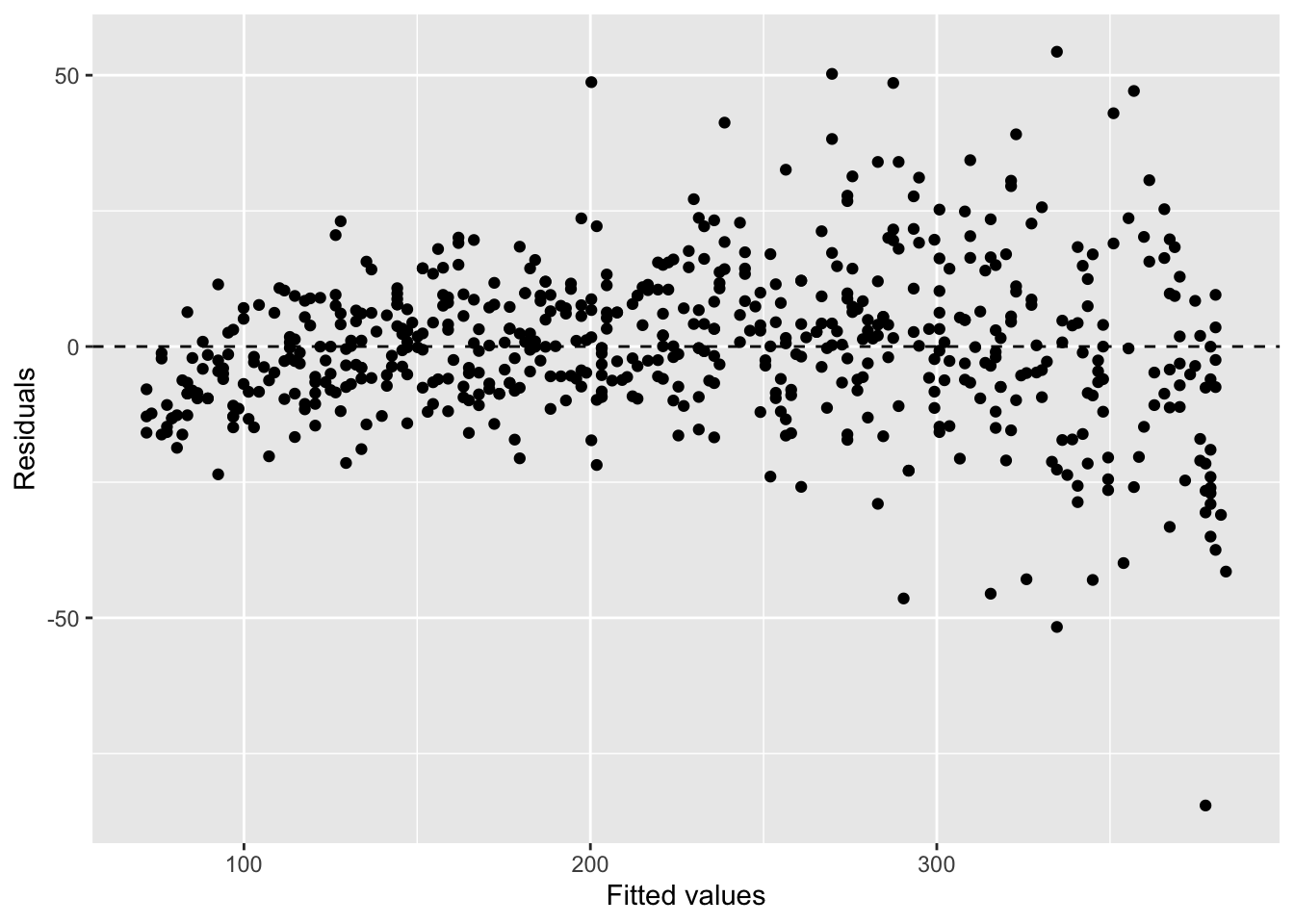
値が大きくなるにつれて、残差のばらつきが大きくなっています。
ggplot(abdom, aes(sample = scale(resid(fit_lm)))) +
stat_qq() +
stat_qq_line() +
labs(x = "Theoretical Quantiles",
y = "Standardized Residuals")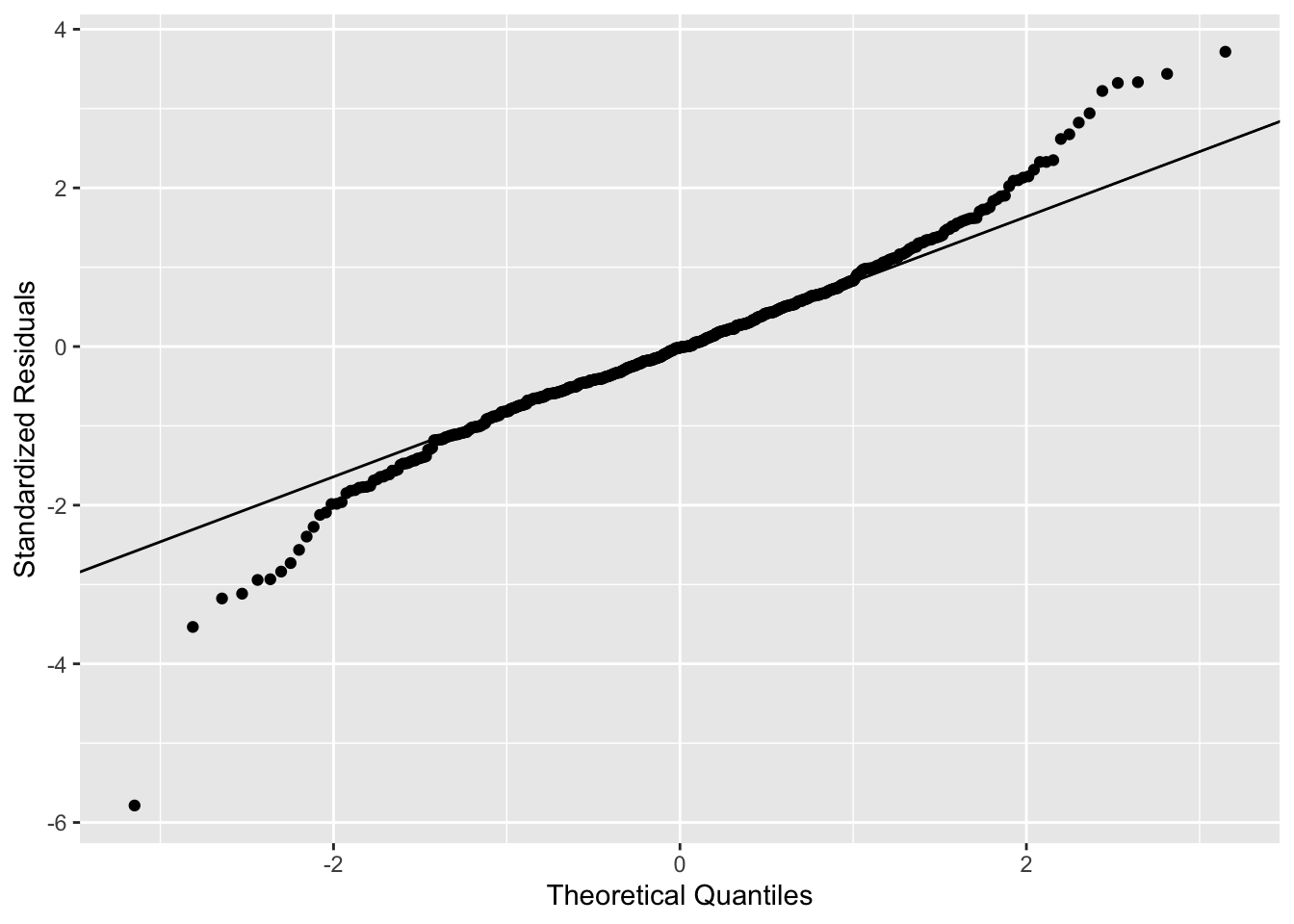
Q-Qプロットを見ると、両端で外れ具合が大きくなっているのがわかります。
GAMLSS
つづいて、GAMLSSであてはめをおこないます。期待値はxのスプライン関数(pb)、分散もxのスプライン関数(pb)でモデル化します。分布はBox-Cox t分布(BCT)を使います。method引数はアルゴリズムの指定で、ここではRigby and StasinopoulosとCole and Greenを組み合わせるようにしています。このあたりは、オンラインマニュアルの例題そのままです。
fit_gamlss <- gamlss(y ~ pb(x), sigma.formula = ~pb(x),
family = BCT, data = abdom,
method = mixed(1, 20))
## GAMLSS-RS iteration 1: Global Deviance = 4771.925
## GAMLSS-CG iteration 1: Global Deviance = 4771.013
## GAMLSS-CG iteration 2: Global Deviance = 4770.994
## GAMLSS-CG iteration 3: Global Deviance = 4770.994
summary(fit_gamlss)
## ******************************************************************
## Family: c("BCT", "Box-Cox t")
##
## Call: gamlss(formula = y ~ pb(x), sigma.formula = ~pb(x),
## family = BCT, data = abdom, method = mixed(1, 20))
##
## Fitting method: mixed(1, 20)
##
## ------------------------------------------------------------------
## Mu link function: identity
## Mu Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -64.44299 1.33397 -48.31 <2e-16 ***
## pb(x) 10.69464 0.05787 184.80 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## ------------------------------------------------------------------
## Sigma link function: log
## Sigma Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.65041 0.10859 -24.407 < 2e-16 ***
## pb(x) -0.01002 0.00380 -2.638 0.00855 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## ------------------------------------------------------------------
## Nu link function: identity
## Nu Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.1072 0.6296 -0.17 0.865
##
## ------------------------------------------------------------------
## Tau link function: log
## Tau Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.4948 0.4261 5.855 7.86e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## ------------------------------------------------------------------
## NOTE: Additive smoothing terms exist in the formulas:
## i) Std. Error for smoothers are for the linear effect only.
## ii) Std. Error for the linear terms maybe are not accurate.
## ------------------------------------------------------------------
## No. of observations in the fit: 610
## Degrees of Freedom for the fit: 11.7603
## Residual Deg. of Freedom: 598.2397
## at cycle: 3
##
## Global Deviance: 4770.994
## AIC: 4794.515
## SBC: 4846.419
## ******************************************************************AICの値は線形モデルよりも小さくなっていました。
診断プロットです。
plot(fit_gamlss)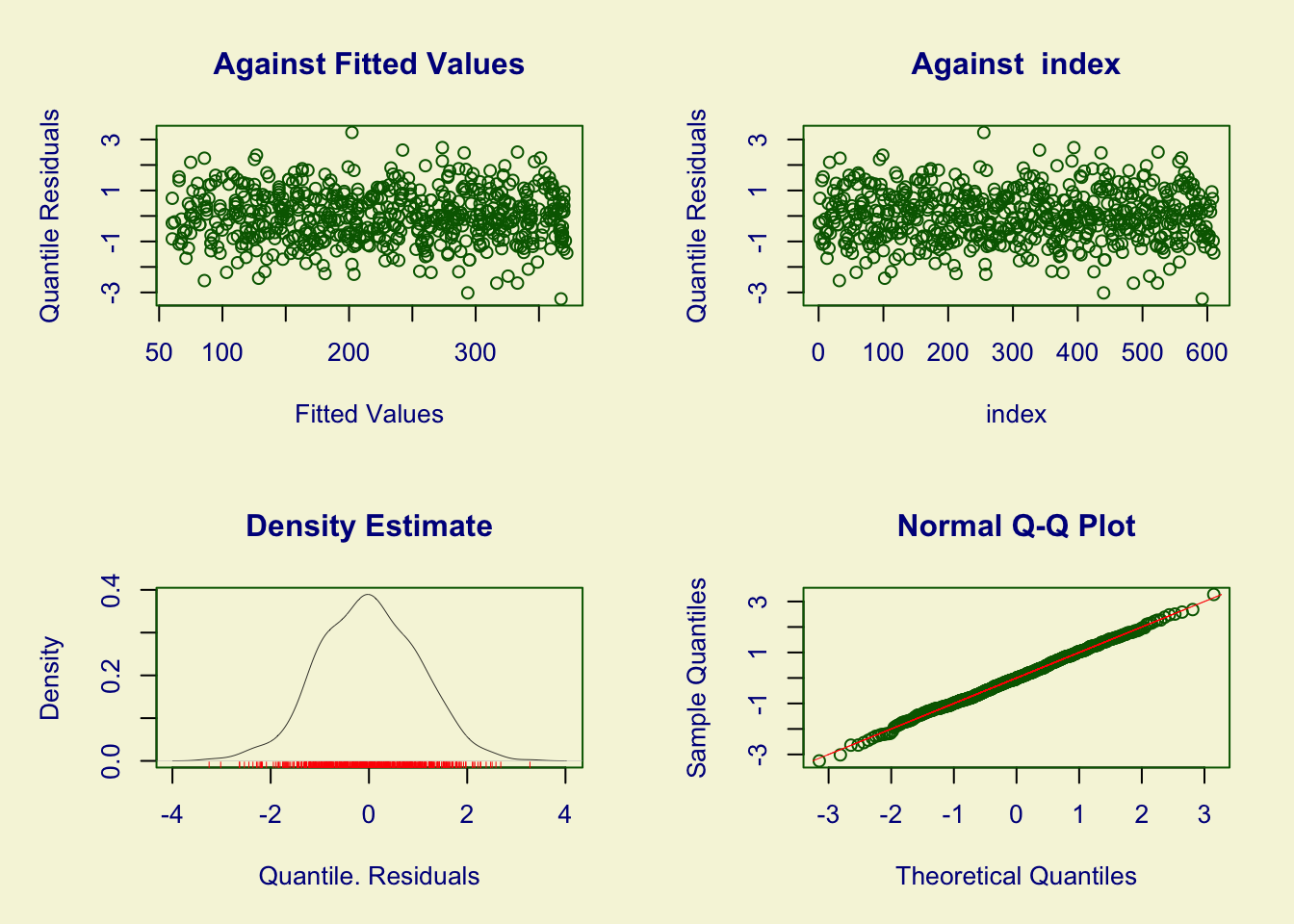
## ******************************************************************
## Summary of the Quantile Residuals
## mean = 0.001237747
## variance = 1.001867
## coef. of skewness = -0.004513695
## coef. of kurtosis = 2.994576
## Filliben correlation coefficient = 0.999324
## ******************************************************************ggplot2でも、Q-Qプロットを作成してみます。
ggplot(abdom, aes(sample = scale(resid(fit_gamlss)))) +
stat_qq() +
stat_qq_line() +
labs(x = "Theoretical Quantiles",
y = "Sample Quantiles")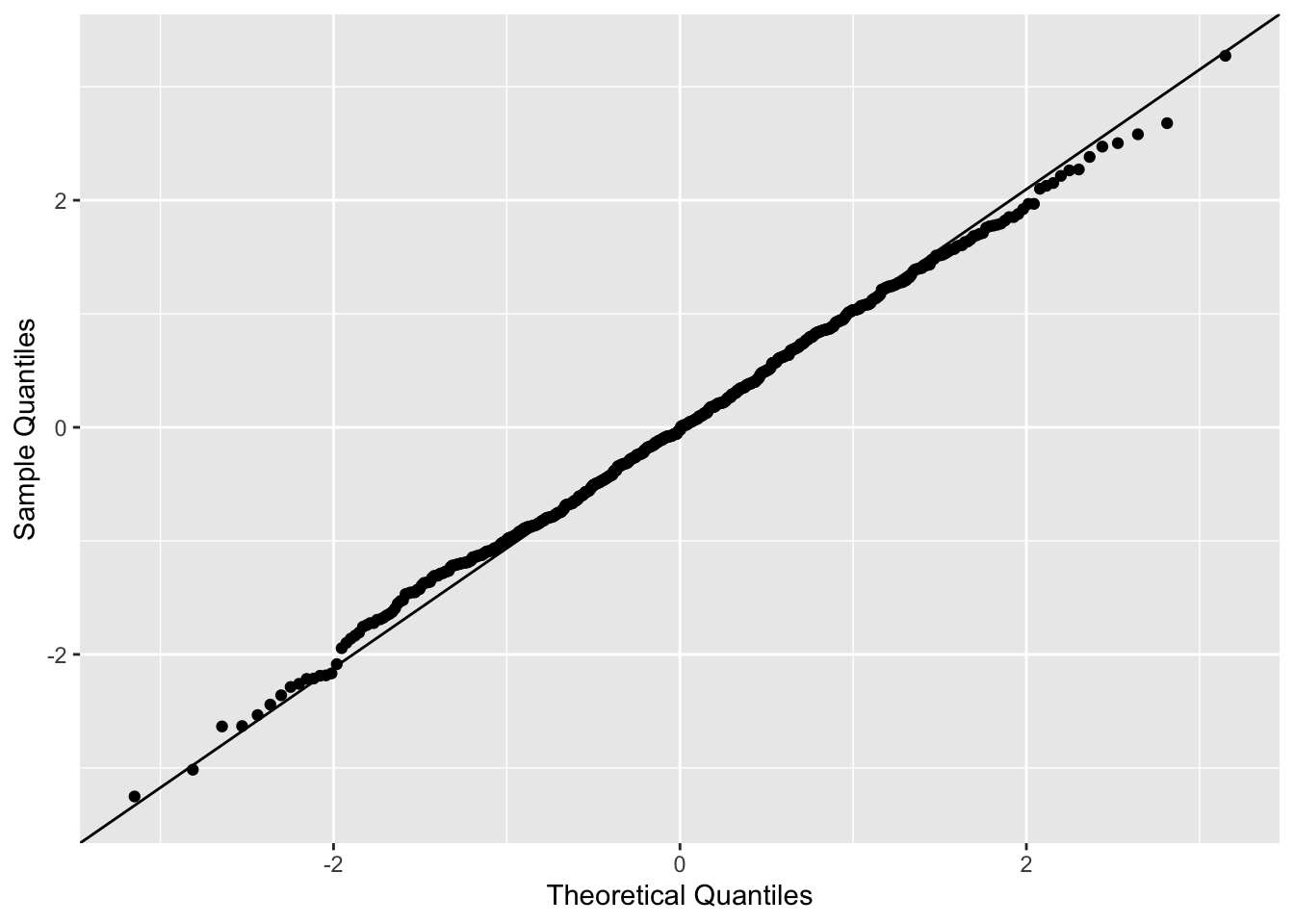
おわりに
GAMLSSについての日本語での解説としては、「GAMLSSとBAMLSSで分布をデータにフィット - 草薙の研究ログ」がありました。こちらでは、単変量の母数の推定と、回帰モデルのあてはめについて解説されています。