Rによる「n個の扉」のモンティ・ホール問題のシミュレーション

※ この記事は、R言語 Advent Calendar 2025の11日目の記事です。

先日から、『パラドックスで学ぶ統計学—相反する分析結果に向き合う—』（岩崎学・川崎玉恵 [著], 共立出版, 2025）を読み始めました。第1章に取り上げられているが「モンティ・ホール問題」で、基本のモンティ・ホール問題のほか、さまざまな変形・拡張版も紹介されています。そのひとつとして1.5.5小節では「n個の扉」版が紹介されています。そこで、この「n個の扉」のシミュレーションをやってみることにしました。

なお、別の変形版モンティ・ホール問題については、2023年のR言語 Advent Calendar 24日目の記事として、@yamamiさんが「【R】司会者の選ぶ箱が偏った時のモンティ・ホール問題」という記事を書いておられます。

通常のモンティ・ホール問題のシミュレーション

「n個の扉」の前に、まずは通常の（3個の扉）のモンティ・ホール問題のシミュレーションからやっていきます。

Rを使っていきますので、グラフ作成のためにggplot2パッケージを、カテゴリカル分布の乱数を使うためにextraDistrパッケージを読み込みます。また、擬似乱数を固定します。

library(ggplot2)
library(extraDistr)
set.seed(123)

関数定義

モンティ・ホール問題をシミュレートする関数を定義します。当たり扉はsample関数で抽出してもよいのですが、当たり扉が偏る場合に拡張できるようにrcat関数を使用しました。

# モンティ・ホール問題をシミュレートする関数
# 引数:
#   select: 出場者が選ぶ扉の番号
#   switch: 司会者が扉を開けた後、スイッチするか
# 返り値: logical, 当たりならばTRUE、外れならばFALSE
monty_hall <- function(select = 1, switch = TRUE) {
  if (select < 1 | select > 3) {
    stop("select は 1〜3 の範囲でなければなりません。")
  }

  # 扉の枚数は3枚
  n <- 3L
  doors <- 1:n
  # 当たりの確率はどの扉も同じとする
  p <- rep(1 / n, n)
  # 当たりの扉をカテゴリカル分布から抽出する
  car <- rcat(1, p)
  # 司会者が開ける扉を決定する
  if (select == car) {
    # 出場者が当たりを選んでいた場合、
    # 外れ扉の中からランダムに1枚開ける
    open <- sample(doors[doors != car], 1)
  } else {
    # 出場者が外れを選んでいた場合は、残りの外れ扉を開ける
    open <- doors[doors != select & doors != car]
  }
  # 出場者が最終的に選ぶ扉を決定する
  if (switch) {
    # スイッチするときは、開いていない扉を選ぶ
    final_select <- doors[doors != select & doors != open]
  } else {
    # スイッチしないときはそのまま
    final_select <- select
  }
  # 最終的に選んだ扉が当たりかどうかを返す
  return(final_select == car)
}

実行例

実行してみます。まずは、扉1を選択して、その後スイッチするという設定です。

monty_hall(select = 1, switch = FALSE)
## [1] FALSE

もう一度実行してみます。第2を選択して、スイッチはしません。

monty_hall(select = 2, switch = TRUE)
## [1] TRUE

シミュレーション

では、当たる確率をシミュレーションで推定します。扉1を選択して、その後スイッチするという設定で、100000回繰り返します。

n_sim <- 100000
replicate(n_sim, monty_hall(select = 1, switch = TRUE)) |>
  mean()
## [1] 0.66688

おおよそ理論値(2/3)に近い値が得られました。

扉1を選択して、その後スイッチしないという設定でもやってみます。

replicate(n_sim, monty_hall(select = 1, switch = FALSE)) |>
  mean()
## [1] 0.33288

こちらも理論値(1/3)に近い値となりました。

グラフ

繰り返しにしたがって、当たりの割合がどのように変化していくのかを見てみました。赤色の点線が理論値です。

n_sim <- 10000
data.frame(x = 1:n_sim,
           y = replicate(n_sim, monty_hall(select = 1, switch = TRUE))) |>
  ggplot(aes(x = x, y = cumsum(y) / x)) +
  geom_line(colour = "blue") +
  geom_hline(yintercept = 2 / 3, linetype = "dashed", colour = "red") +
  ylim(0, 1) +
  labs(x = "シミュレーション回数", y = "当たりの割合") +
  theme_classic(base_family = "Noto Sans JP", base_size = 10)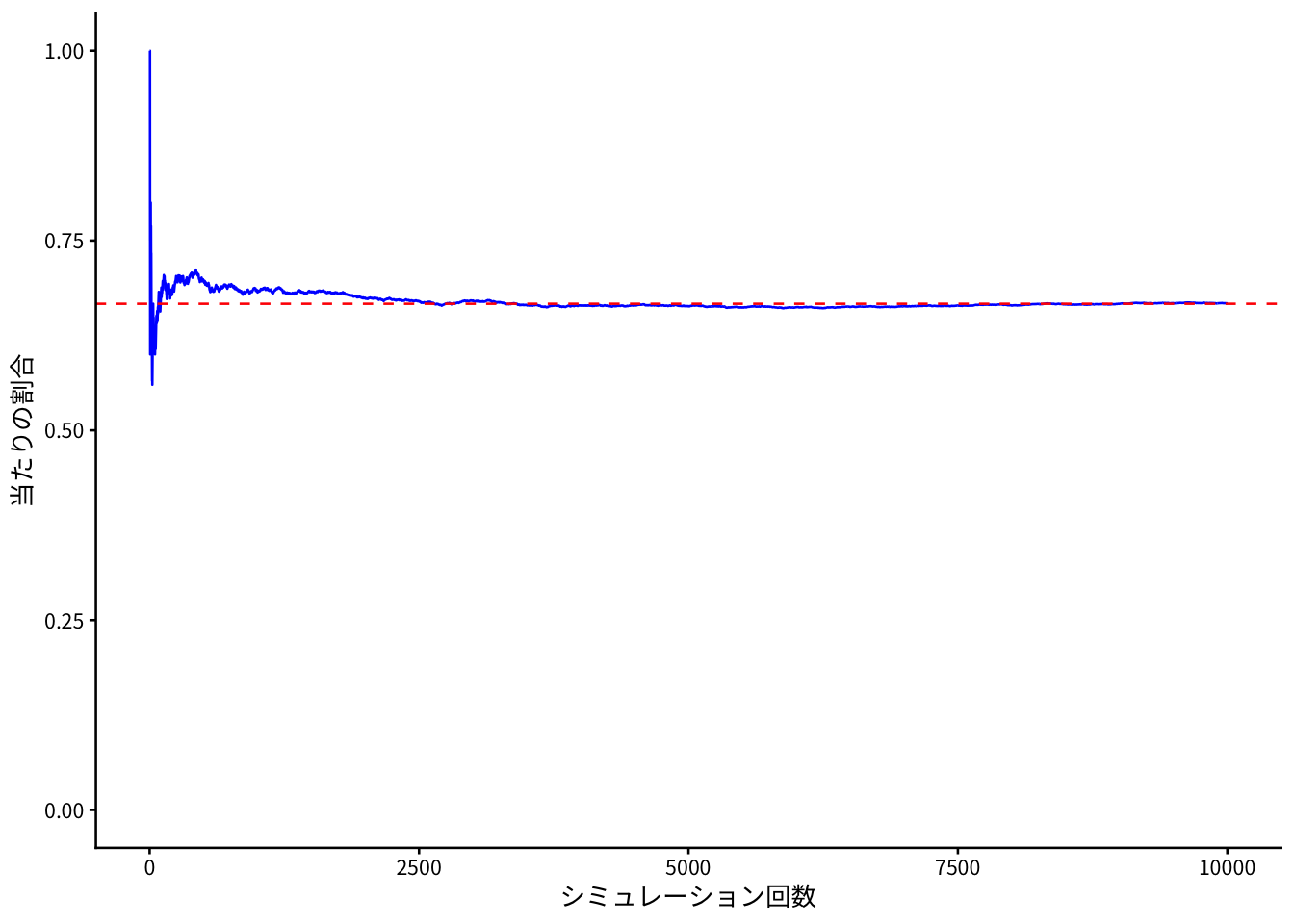

シミュレーション回数が増えるにしたがって理論値に近づいていきます。

「n個の扉」の場合

次に、扉がn枚あり、司会者がr枚の外れ扉を開けるという設定のシミュレーションをやってみます。まずはその関数を定義します。あまり最適化していないので、遅いと思われます。

# モンティ・ホール問題をシミュレートする関数
# 扉がn枚あり、司会者がr枚の外れ扉を開ける場合
# 引数:
#   n:      扉の数
#   r:      司会者が開ける扉の数 (r <= n - 2)
#   select: 出場者が選ぶ扉の番号
#   switch: 司会者が扉を開けた後、スイッチするか
# 返り値: logical, 当たりならばTRUE、外れならばFALSE
monty_hall_n <- function(n = 3L, r = n - 2L,
                         select = 1L, switch = TRUE) {
  if (n < 3) {
    stop("n >= 3 でなければなりません。") 
  }
  if (r < 1 | r > n - 2) {
    stop("1 <= r <= n - 2 でなければなりません。")
  }
  if (select < 1 | select > n) {
    stop("1 <= select <= n でなければなりません。")
  }

  # 扉の枚数はn枚
  doors <- 1L:n
  # 当たりの確率はどの扉も同じとする
  p <- rep(1 / n, n)
  # 当たりの扉をカテゴリカル分布から抽出する
  car <- rcat(1, p)
  # 司会者が開ける扉の候補
  # 当たりと出場者の選択以外
  can_door <- setdiff(doors, c(car, select))
  # 司会者が開ける扉を決定する
  if (length(can_door) == 1) {
    # 候補が1個のときはそれに決定
    open <- can_door
  } else {
    # 2個以上のときはランダムにr個を開ける
    open <- sample(can_door, r)
  }
  # 出場者が最終的に選ぶ扉を決定する
  if (switch) {
    # スイッチするとき
    # スイッチ先の候補は、最初の選択と空いている扉以外
    can_door <- setdiff(doors, c(select, open))
    if (length(can_door) == 1) {
      # 候補が1個のときはそれに決定
      final_select <- can_door
    } else {
      # 候補が複数あれば、ランダムに選ぶ
      final_select <- sample(can_door, 1)
    }
  } else {
    # スイッチしないときはそのまま
    final_select <- select
  }
  # 最終的に選んだ扉が当たりかどうかを返す
  return(final_select == car)
}

扉が4枚で、出場者は扉1を選択し、司会者は2個の扉を開け、出場者はその後スイッチするという設定でシミュレーションを実行し、当たり確率を推定します。

n_sim <- 100000
replicate(n_sim, monty_hall_n(n = 4, r = 2,
                              select = 1, switch = TRUE)) |>
  mean()
## [1] 0.7513

本の説明によると、n 枚の扉があり、r 枚の外れ扉を開ける場合の当たりの確率の理論値は (n - 1) / {n(n - r - 1)} です。したがって、n = 4, r = 2 のときの当たり確率は (4 - 1) / {(4 * (4 - 2 - 1)} = 3/4 です。シミュレーションの結果は、理論値に近い値でした。

nを順番に変えてシミュレーション

n を 3, 4,.., 100と変化させ、r は n-2 としたときの当たりの割合をグラフで表示します。

繰り返しは、parallelパッケージのmclapply関数を使用して並列化しています。この関数はforkを使っているので、Windowsでは動作しません。

library(parallel)

# シミュレーション用の関数を定義します
# 引数:
#   n: 扉の数
#   select: 出場者が選ぶ扉の番号
#   switch: 司会者が扉を開けた後、スイッチするか
#   n_sim: ひとつのnについての繰り返し回数
# 返り値: numeric, 当たりの割合
sim_fun <- function(n, select = 1, switch = TRUE, n_sim = 100000) {
  replicate(n_sim, monty_hall_n(select = select, switch = switch,
                                n = n, r = n - 2)) |>
    mean()
}

# mclapplyで並列化
n <- 3:100
result <- mclapply(n, function(n) sim_fun(n),
                   mc.cores = detectCores()) |>
  unlist()

data.frame(n = n, pr = result) |>
  ggplot(aes(x = n, y = pr)) +
  geom_line(colour = "blue") +
  geom_hline(yintercept = 1, linewidth = 0.5,
             colour = "gray") +
  ylim(0.6, 1) +
  labs(x = "扉の数", y = "当たりの割合") +
  theme_classic(base_family = "Noto Sans JP", base_size = 10)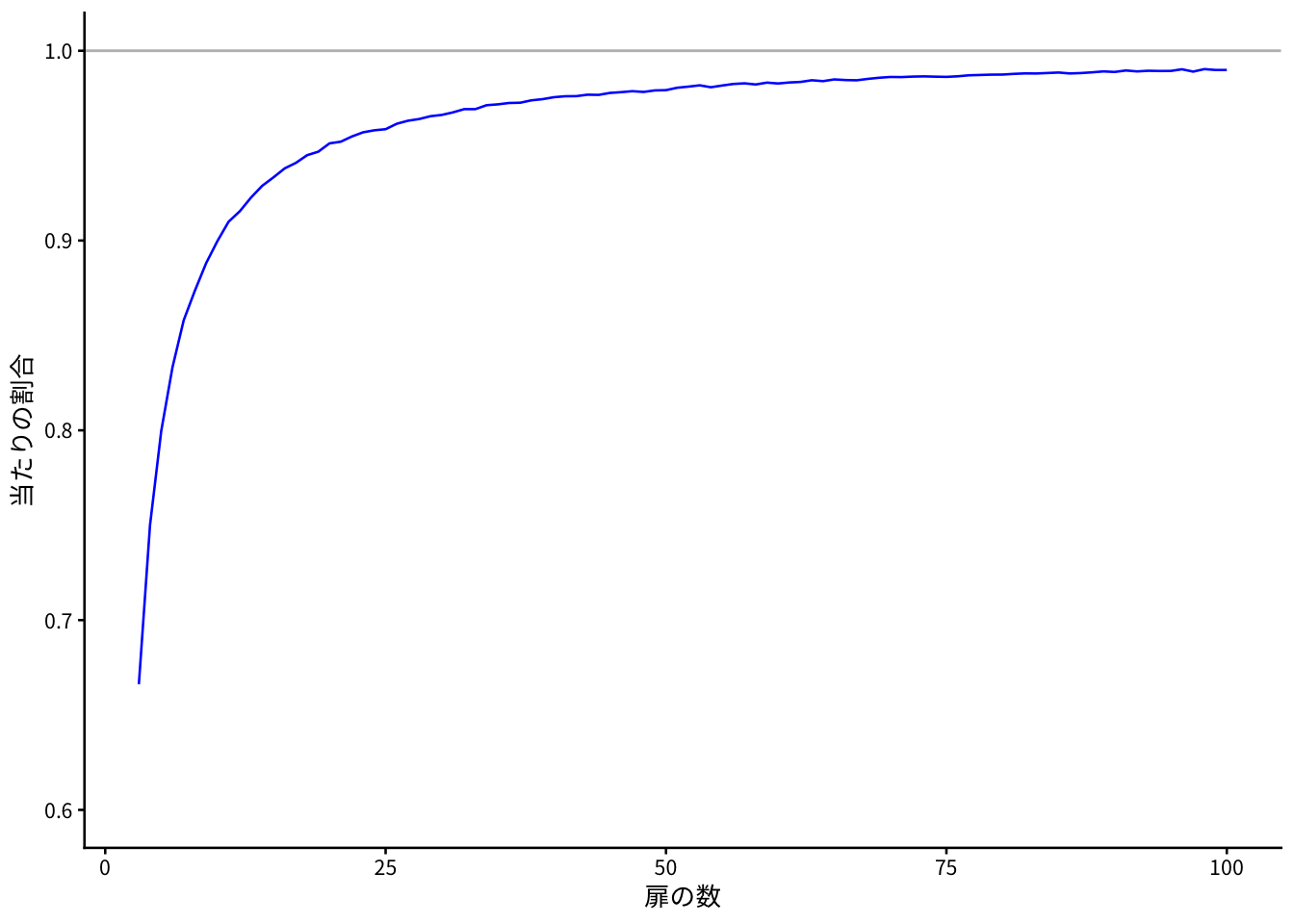

理論値の(n-1)/nに近い値になっているようです。